课程五(Sequence Models),第三周(Sequence models & Attention mechanism) —— 1.Programming assignments:Neural Machine Translation with Attention
Neural Machine Translation
Welcome to your first programming assignment for this week!
You will build a Neural Machine Translation (NMT) model to translate human readable dates ("25th of June, 2009") into machine readable dates ("2009-06-25"). You will do this using an attention model, one of the most sophisticated sequence to sequence models.
This notebook was produced together with NVIDIA's Deep Learning Institute.
Let's load all the packages you will need for this assignmen.
【code】
from keras.layers import Bidirectional, Concatenate, Permute, Dot, Input, LSTM, Multiplyfrom keras.layers import RepeatVector, Dense, Activation, Lambdafrom keras.optimizers import Adamfrom keras.utils import to_categoricalfrom keras.models import load_model, Modelimport keras.backend as Kimport numpy as npfrom faker import Fakerimport randomfrom tqdm import tqdmfrom babel.dates import format_datefrom nmt_utils import *import matplotlib.pyplot as plt%matplotlib inline |
1 - Translating human readable dates into machine readable dates
The model you will build here could be used to translate from one language to another, such as translating from English to Hindi. However, language translation requires massive datasets and usually takes days of training on GPUs. To give you a place to experiment with these models even without using massive datasets, we will instead use a simpler "date translation" task.
The network will input a date written in a variety of possible formats (e.g. "the 29th of August 1958", "03/30/1968", "24 JUNE 1987") and translate them into standardized, machine readable dates (e.g. "1958-08-29", "1968-03-30", "1987-06-24"). We will have the network learn to output dates in the common machine-readable format YYYY-MM-DD.
1.1 - Dataset
We will train the model on a dataset of 10000 human readable dates and their equivalent, standardized, machine readable dates. Let's run the following cells to load the dataset and print some examples.
【code】
m = 10000dataset, human_vocab, machine_vocab, inv_machine_vocab = load_dataset(m) |
dataset[:10] |
【result】
[('9 may 1998', '1998-05-09'), ('10.09.70', '1970-09-10'), ('4/28/90', '1990-04-28'), ('thursday january 26 1995', '1995-01-26'), ('monday march 7 1983', '1983-03-07'), ('sunday may 22 1988', '1988-05-22'), ('tuesday july 8 2008', '2008-07-08'), ('08 sep 1999', '1999-09-08'), ('1 jan 1981', '1981-01-01'), ('monday may 22 1995', '1995-05-22')] |
You've loaded:
dataset: a list of tuples of (human readable date, machine readable date)human_vocab: a python dictionary mapping all characters used in the human readable dates to an integer-valued indexmachine_vocab: a python dictionary mapping all characters used in machine readable dates to an integer-valued index. These indices are not necessarily consistent withhuman_vocab.inv_machine_vocab: the inverse dictionary ofmachine_vocab, mapping from indices back to characters.
Let's preprocess the data and map the raw text data into the index values. We will also use Tx=30 (which we assume is the maximum length of the human readable date; if we get a longer input, we would have to truncate it) and Ty=10 (since "YYYY-MM-DD" is 10 characters long).
【中文翻译】
您已加载:
dataset: (人类可读日期, 机器可读日期) 的元组列表
human_vocab: python 字典将人类可读日期中使用的所有字符映射为整数值索引
machine_vocab: python 字典将机器可读日期中使用的所有字符映射到整数值索引。这些指数不一定与 human_vocab 一致。
inv_machine_vocab: machine_vocab 的逆字典, 从索引返回到字符的映射。
让我们对数据进行预处理, 并将原始文本数据映射到索引值中。我们也将使用 Tx=30 (我们假设是人类可读日期的最大长度; 如果我们得到一个更长的输入, 我们将不得不截断它) 和 Ty=10 (因为 "YYYY-MM-DD" 是10个字符长)。
【code】
Tx = 30Ty = 10X, Y, Xoh, Yoh = preprocess_data(dataset, human_vocab, machine_vocab, Tx, Ty)print("X.shape:", X.shape)print("Y.shape:", Y.shape)print("Xoh.shape:", Xoh.shape)print("Yoh.shape:", Yoh.shape) |
【result】
X.shape: (10000, 30)Y.shape: (10000, 10)Xoh.shape: (10000, 30, 37)Yoh.shape: (10000, 10, 11) |
You now have:
X: a processed version of the human readable dates in the training set, where each character is replaced by an index mapped to the character viahuman_vocab. Each date is further padded to Tx values with a special character (< pad >).X.shape = (m, Tx)Y: a processed version of the machine readable dates in the training set, where each character is replaced by the index it is mapped to inmachine_vocab. You should haveY.shape = (m, Ty).Xoh: one-hot version ofX, the "1" entry's index is mapped to the character thanks tohuman_vocab.Xoh.shape = (m, Tx, len(human_vocab))Yoh: one-hot version ofY, the "1" entry's index is mapped to the character thanks tomachine_vocab.Yoh.shape = (m, Tx, len(machine_vocab)). Here,len(machine_vocab) = 11since there are 11 characters ('-' as well as 0-9).
【中文翻译】
您现在有:
X: 训练集中的被人可读的日期的一个经过处理的版本, 其中每个字符都由通过 human_vocab 映射到该字符的索引替换。将每个日期进一步由特殊字符 (< pad >)填充为Tx 长度。X.shape = (m, Tx)
Y: 在训练集中的被机器可读的日期的一个经过处理的版本, 其中每个字符被由映射到 machine_vocab 中的索引替换。Y.shape = (m, Ty)。
Xoh: one-hot版本的 X, "1 " 条目的索引映射到字符, 多亏了 human_vocab. Xoh.shape = (m, Tx, len(human_vocab))
Yoh: ne-hot版本的 Y, "1 " 条目的索引被映射到字符, 多亏了 machine_vocab. Yoh.shape = (m, Tx, len(machine_vocab))。这里, len (machine_vocab) = 11, 因为有11个字符 ('-' 并且 0-9)。
Lets also look at some examples of preprocessed training examples. Feel free to play with index in the cell below to navigate the dataset and see how source/target dates are preprocessed.
【code】
index = 0print("Source date:", dataset[index][0])print("Target date:", dataset[index][1])print()print("Source after preprocessing (indices):", X[index])print("Target after preprocessing (indices):", Y[index])print()print("Source after preprocessing (one-hot):", Xoh[index])print("Target after preprocessing (one-hot):", Yoh[index]) |
【result】
Source date: 9 may 1998Target date: 1998-05-09Source after preprocessing (indices): [12 0 24 13 34 0 4 12 12 11 36 36 36 36 36 36 36 36 36 36 36 36 36 36 36 36 36 36 36 36]Target after preprocessing (indices): [ 2 10 10 9 0 1 6 0 1 10]Source after preprocessing (one-hot): [[ 0. 0. 0. ..., 0. 0. 0.] [ 1. 0. 0. ..., 0. 0. 0.] [ 0. 0. 0. ..., 0. 0. 0.] ..., [ 0. 0. 0. ..., 0. 0. 1.] [ 0. 0. 0. ..., 0. 0. 1.] [ 0. 0. 0. ..., 0. 0. 1.]]Target after preprocessing (one-hot): [[ 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0.] [ 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0.] [ 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]] |
2 - Neural machine translation with attention
If you had to translate a book's paragraph from French to English, you would not read the whole paragraph, then close the book and translate. Even during the translation process, you would read/re-read and focus on the parts of the French paragraph corresponding to the parts of the English you are writing down.
The attention mechanism tells a Neural Machine Translation model where it should pay attention to at any step.
【中文翻译】
2- 注意力机制的神经网络的机器翻译
如果你必须把一本书的段落从法语翻译成英语, 你不会读完整个段落, 然后把书合上并翻译。即使在翻译过程中, 你也会阅读/重新阅读和关注与你写下的英语部分相应的法语段落部分。
attention机制告诉一个神经网络的机器翻译模型, 在每一步它应该注意什么。
2.1 - Attention mechanism
In this part, you will implement the attention mechanism presented in the lecture videos. Here is a figure to remind you how the model works. The diagram on the left shows the attention model. The diagram on the right shows what one "Attention" step does to calculate the attention variables <span id="MathJax-Span-7" class="mrow"><span id="MathJax-Span-8" class="msubsup"><span id="MathJax-Span-9" class="mi">α<sup><span id="MathJax-Span-10" class="texatom"><span id="MathJax-Span-11" class="mrow"><span id="MathJax-Span-12" class="mo">⟨<span id="MathJax-Span-13" class="mi">t<span id="MathJax-Span-14" class="mo">,<span id="MathJax-Span-15" class="msup"><span id="MathJax-Span-16" class="mi">t<span id="MathJax-Span-17" class="mo">′<span id="MathJax-Span-18" class="mo">⟩, which are used to compute the context variable <span id="MathJax-Span-20" class="mrow"><span id="MathJax-Span-21" class="mi">c<span id="MathJax-Span-22" class="mi">o<span id="MathJax-Span-23" class="mi">n<span id="MathJax-Span-24" class="mi">t<span id="MathJax-Span-25" class="mi">e<span id="MathJax-Span-26" class="mi">x<span id="MathJax-Span-27" class="msubsup"><span id="MathJax-Span-28" class="mi">t<sup><span id="MathJax-Span-29" class="texatom"><span id="MathJax-Span-30" class="mrow"><span id="MathJax-Span-31" class="mo">⟨<span id="MathJax-Span-32" class="mi">t<span id="MathJax-Span-33" class="mo">⟩ for each timestep in the output (<span id="MathJax-Span-35" class="mrow"><span id="MathJax-Span-36" class="mi">t<span id="MathJax-Span-37" class="mo">=<span id="MathJax-Span-38" class="mn">1<span id="MathJax-Span-39" class="mo">,<span id="MathJax-Span-40" class="mo">…<span id="MathJax-Span-41" class="mo">,<span id="MathJax-Span-42" class="msubsup"><span id="MathJax-Span-43" class="mi">T<sub><span id="MathJax-Span-44" class="mi">y).
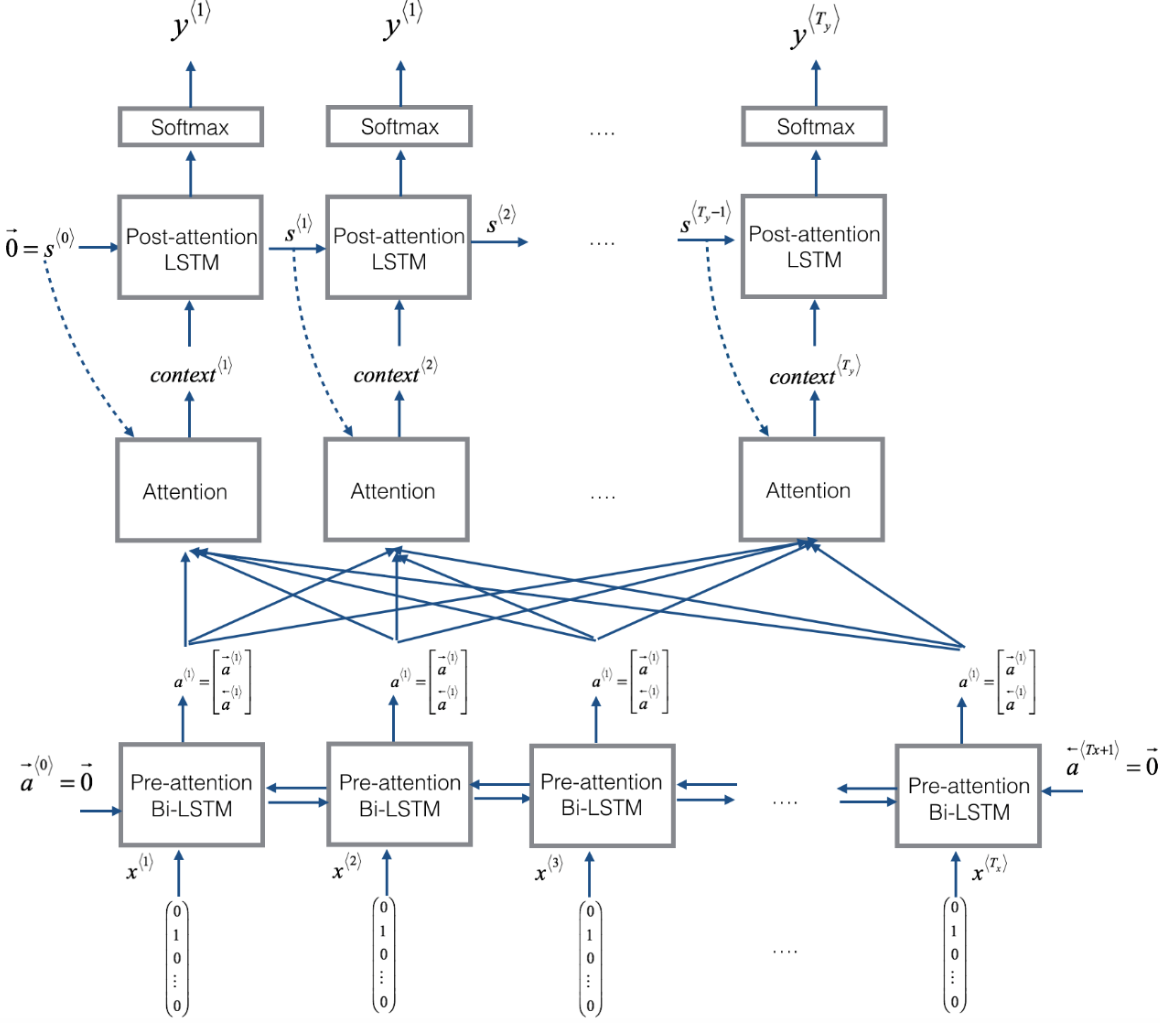
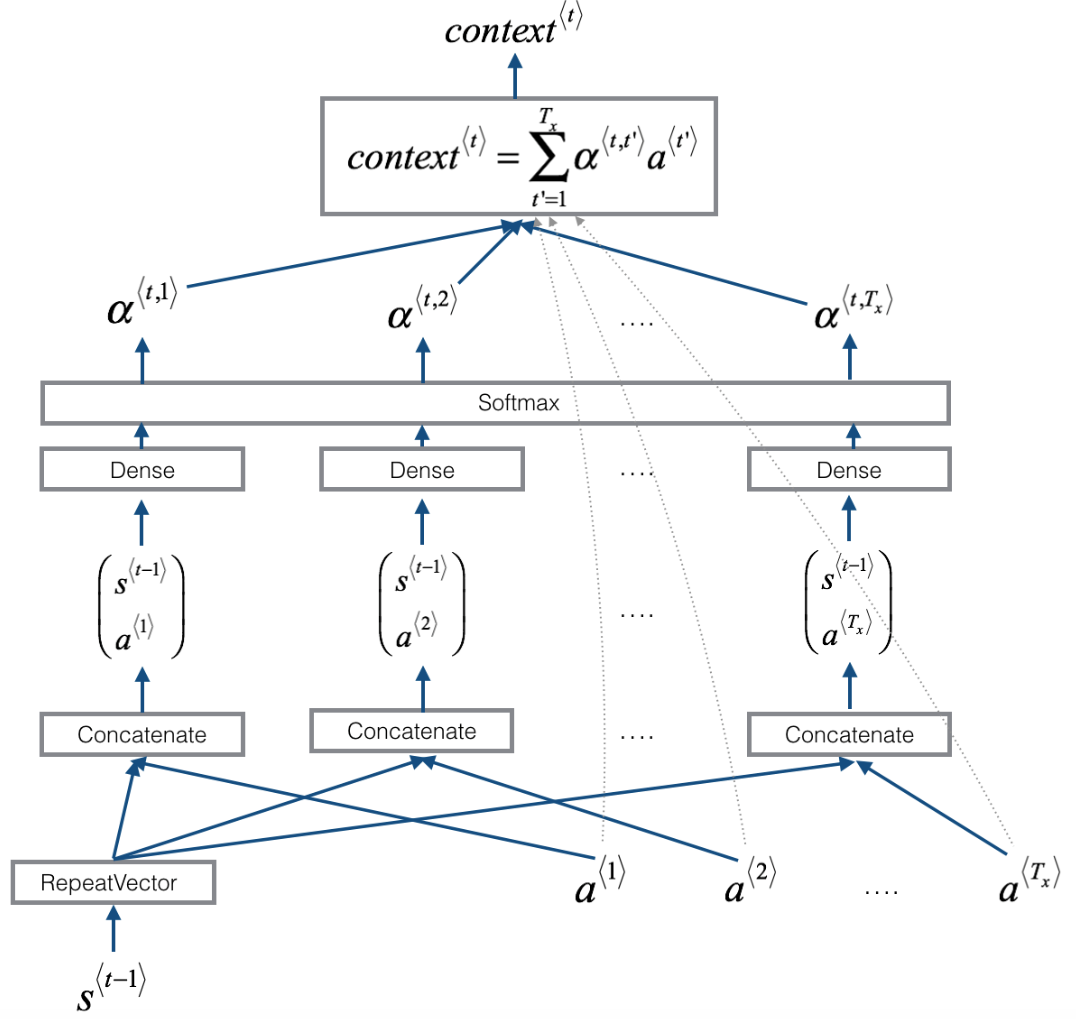
Figure 1: Neural machine translation with attention
Here are some properties of the model that you may notice:
-
There are two separate LSTMs in this model (see diagram on the left). Because the one at the bottom of the picture is a Bi-directional LSTM and comes before the attention mechanism, we will call it pre-attention Bi-LSTM. The LSTM at the top of the diagram comes after the attention mechanism, so we will call it the post-attention LSTM. The pre-attention Bi-LSTM goes through <span id="MathJax-Span-46" class="mrow"><span id="MathJax-Span-47" class="msubsup"><span id="MathJax-Span-48" class="mi">T<sub><span id="MathJax-Span-49" class="mi">x time steps; the post-attention LSTM goes through <span id="MathJax-Span-51" class="mrow"><span id="MathJax-Span-52" class="msubsup"><span id="MathJax-Span-53" class="mi">T<span id="MathJax-Span-54" class="mi"><sub>y</sub> time steps.
-
The post-attention LSTM passes <span id="MathJax-Span-56" class="mrow"><span id="MathJax-Span-57" class="msubsup"><span id="MathJax-Span-58" class="mi">s<span id="MathJax-Span-59" class="texatom"><span id="MathJax-Span-60" class="mrow"><span id="MathJax-Span-61" class="mo"><sup>⟨</sup><span id="MathJax-Span-62" class="mi"><sup>t</sup><span id="MathJax-Span-63" class="mo"><sup>⟩</sup><span id="MathJax-Span-64" class="mo">,<span id="MathJax-Span-65" class="msubsup"><span id="MathJax-Span-66" class="mi">c<sup><span id="MathJax-Span-67" class="texatom"><span id="MathJax-Span-68" class="mrow"><span id="MathJax-Span-69" class="mo">⟨<span id="MathJax-Span-70" class="mi">t<span id="MathJax-Span-71" class="mo">⟩ from one time step to the next. In the lecture videos, we were using only a basic RNN for the post-activation sequence model, so the state captured by the RNN output activations <span id="MathJax-Span-73" class="mrow"><span id="MathJax-Span-74" class="msubsup"><span id="MathJax-Span-75" class="mi">s<sup><span id="MathJax-Span-76" class="texatom"><span id="MathJax-Span-77" class="mrow"><span id="MathJax-Span-78" class="mo">⟨<span id="MathJax-Span-79" class="mi">t<span id="MathJax-Span-80" class="mo">⟩. But since we are using an LSTM here, the LSTM has both the output activation <span id="MathJax-Span-82" class="mrow"><span id="MathJax-Span-83" class="msubsup"><span id="MathJax-Span-84" class="mi">s<sup><span id="MathJax-Span-85" class="texatom"><span id="MathJax-Span-86" class="mrow"><span id="MathJax-Span-87" class="mo">⟨<span id="MathJax-Span-88" class="mi">t<span id="MathJax-Span-89" class="mo">⟩ and the hidden cell state <span id="MathJax-Span-91" class="mrow"><span id="MathJax-Span-92" class="msubsup"><span id="MathJax-Span-93" class="mi">c<sup><span id="MathJax-Span-94" class="texatom"><span id="MathJax-Span-95" class="mrow"><span id="MathJax-Span-96" class="mo">⟨<span id="MathJax-Span-97" class="mi">t<span id="MathJax-Span-98" class="mo">⟩. However, unlike previous text generation examples (such as Dinosaurus in week 1), in this model the post-activation LSTM at time <span id="MathJax-Span-100" class="mrow"><span id="MathJax-Span-101" class="mi">t does will not take the specific generated <span id="MathJax-Span-103" class="mrow"><span id="MathJax-Span-104" class="msubsup"><span id="MathJax-Span-105" class="mi">y<sup><span id="MathJax-Span-106" class="texatom"><span id="MathJax-Span-107" class="mrow"><span id="MathJax-Span-108" class="mo">⟨<span id="MathJax-Span-109" class="mi">t<span id="MathJax-Span-110" class="mo">−<span id="MathJax-Span-111" class="mn">1<span id="MathJax-Span-112" class="mo">⟩ as input; it only takes <span id="MathJax-Span-114" class="mrow"><span id="MathJax-Span-115" class="msubsup"><span id="MathJax-Span-116" class="mi">s<sup><span id="MathJax-Span-117" class="texatom"><span id="MathJax-Span-118" class="mrow"><span id="MathJax-Span-119" class="mo">⟨<span id="MathJax-Span-120" class="mi">t<span id="MathJax-Span-121" class="mo">⟩ and <span id="MathJax-Span-123" class="mrow"><span id="MathJax-Span-124" class="msubsup"><span id="MathJax-Span-125" class="mi">c<sup><span id="MathJax-Span-126" class="texatom"><span id="MathJax-Span-127" class="mrow"><span id="MathJax-Span-128" class="mo">⟨<span id="MathJax-Span-129" class="mi">t<span id="MathJax-Span-130" class="mo">⟩ as input. We have designed the model this way, because (unlike language generation where adjacent characters are highly correlated) there isn't as strong a dependency between the previous character and the next character in a YYYY-MM-DD date.
-
We use
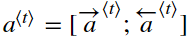 to represent the concatenation of the activations of both the forward-direction and backward-directions of the pre-attention Bi-LSTM.
to represent the concatenation of the activations of both the forward-direction and backward-directions of the pre-attention Bi-LSTM. -
The diagram on the right uses a
RepeatVectornode to copy <span id="MathJax-Span-163" class="mrow"><span id="MathJax-Span-164" class="msubsup"><span id="MathJax-Span-165" class="mi">s<sup><span id="MathJax-Span-166" class="texatom"><span id="MathJax-Span-167" class="mrow"><span id="MathJax-Span-168" class="mo">⟨<span id="MathJax-Span-169" class="mi">t<span id="MathJax-Span-170" class="mo">−<span id="MathJax-Span-171" class="mn">1<span id="MathJax-Span-172" class="mo">⟩'s value <span id="MathJax-Span-174" class="mrow"><span id="MathJax-Span-175" class="msubsup"><span id="MathJax-Span-176" class="mi">T<sub><span id="MathJax-Span-177" class="mi">x times, and thenConcatenationto concatenate <span id="MathJax-Span-179" class="mrow"><span id="MathJax-Span-180" class="msubsup"><span id="MathJax-Span-181" class="mi">s<sup><span id="MathJax-Span-182" class="texatom"><span id="MathJax-Span-183" class="mrow"><span id="MathJax-Span-184" class="mo">⟨<span id="MathJax-Span-185" class="mi">t<span id="MathJax-Span-186" class="mo">−<span id="MathJax-Span-187" class="mn">1<span id="MathJax-Span-188" class="mo">⟩ and <span id="MathJax-Span-190" class="mrow"><span id="MathJax-Span-191" class="msubsup"><span id="MathJax-Span-192" class="mi">a<sup><span id="MathJax-Span-193" class="texatom"><span id="MathJax-Span-194" class="mrow"><span id="MathJax-Span-195" class="mo">⟨<span id="MathJax-Span-196" class="mi">t<span id="MathJax-Span-197" class="mo">⟩ to compute <span id="MathJax-Span-199" class="mrow"><span id="MathJax-Span-200" class="msubsup"><span id="MathJax-Span-201" class="mi">e<sup><span id="MathJax-Span-202" class="texatom"><span id="MathJax-Span-203" class="mrow"><span id="MathJax-Span-204" class="mo">⟨<span id="MathJax-Span-205" class="mi">t<span id="MathJax-Span-206" class="mo">,<span id="MathJax-Span-207" class="msup"><span id="MathJax-Span-208" class="mi">t<span id="MathJax-Span-209" class="mo">′⟩, which is then passed through a softmax to compute <span id="MathJax-Span-211" class="mrow"><span id="MathJax-Span-212" class="msubsup"><span id="MathJax-Span-213" class="mi">α<sup><span id="MathJax-Span-214" class="texatom"><span id="MathJax-Span-215" class="mrow"><span id="MathJax-Span-216" class="mo">⟨<span id="MathJax-Span-217" class="mi">t<span id="MathJax-Span-218" class="mo">,<span id="MathJax-Span-219" class="msup"><span id="MathJax-Span-220" class="mi">t<span id="MathJax-Span-221" class="mo">′<span id="MathJax-Span-222" class="mo">⟩. We'll explain how to useRepeatVectorandConcatenationin Keras below.
【中文翻译】
下面是您可能注意到的模型的一些属性:
- 此模型中有两个单独的 LSTMs (请参见左侧的图示)。因为在图片底部的一个是双向 LSTM, 并出现在attention机制之前, 所以我们将它称为 "pre-attention Bi-LSTM"。在图的顶端的LSTM 是在attention机制之后, 所以我们将它称为post-attention LSTM。The pre-attention Bi-LSTM通过 Tx时间步骤;the post-attention LSTM 通过 Ty 时间步骤。
- The post-attention LSTM通过 s⟨t⟩,c⟨t⟩从一个时间步骤到下一个。在讲座视频中, 我们只使用了the post-activation sequence model的基本 RNN, 因此 RNN 输出激活 <span id="MathJax-Span-73" class="mrow"><span id="MathJax-Span-74" class="msubsup"><span id="MathJax-Span-75" class="mi">s<sup><span id="MathJax-Span-76" class="texatom"><span id="MathJax-Span-77" class="mrow"><span id="MathJax-Span-78" class="mo">⟨<span id="MathJax-Span-79" class="mi">t<span id="MathJax-Span-80" class="mo">⟩捕获的状态。但是, 由于我们在这里使用的 LSTM, LSTM 有输出激活 <span id="MathJax-Span-73" class="mrow"><span id="MathJax-Span-74" class="msubsup"><span id="MathJax-Span-75" class="mi">s<sup><span id="MathJax-Span-76" class="texatom"><span id="MathJax-Span-77" class="mrow"><span id="MathJax-Span-78" class="mo">⟨<span id="MathJax-Span-79" class="mi">t<span id="MathJax-Span-80" class="mo">⟩和隐藏的细胞状态 c⟨t⟩。但是, 与以前的文本生成示例 (如1周中的 Dinosaurus) 不同, 在这个模型中, the post-activation LSTM在t时刻将不会被 <span id="MathJax-Span-103" class="mrow"><span id="MathJax-Span-104" class="msubsup"><span id="MathJax-Span-105" class="mi">y<sup><span id="MathJax-Span-106" class="texatom"><span id="MathJax-Span-107" class="mrow"><span id="MathJax-Span-108" class="mo">⟨<span id="MathJax-Span-109" class="mi">t<span id="MathJax-Span-110" class="mo">−<span id="MathJax-Span-111" class="mn">1<span id="MathJax-Span-112" class="mo">⟩ 作为输入;它只需要 <span id="MathJax-Span-114" class="mrow"><span id="MathJax-Span-115" class="msubsup"><span id="MathJax-Span-116" class="mi">s<sup><span id="MathJax-Span-117" class="texatom"><span id="MathJax-Span-118" class="mrow"><span id="MathJax-Span-119" class="mo">⟨<span id="MathJax-Span-120" class="mi">t<span id="MathJax-Span-121" class="mo">⟩ 和 <span id="MathJax-Span-123" class="mrow"><span id="MathJax-Span-124" class="msubsup"><span id="MathJax-Span-125" class="mi">c<sup><span id="MathJax-Span-126" class="texatom"><span id="MathJax-Span-127" class="mrow"><span id="MathJax-Span-128" class="mo">⟨<span id="MathJax-Span-129" class="mi">t<span id="MathJax-Span-130" class="mo">⟩作为输入。我们用这种方式设计了这个模型, 因为 (与相邻字符高度关联的语言生成不同), 以前的字符和在一个日期内的下一个字符之间没有太强的依赖性。
- 我们使用
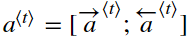 来表示the pre-attention Bi-LSTM的向前方向和向后方向的激活的串联。
来表示the pre-attention Bi-LSTM的向前方向和向后方向的激活的串联。 - 右侧的关系图使用 RepeatVector 节点复制s⟨t−1⟩的值 Tx次, 然后串联以连接 <span id="MathJax-Span-179" class="mrow"><span id="MathJax-Span-180" class="msubsup"><span id="MathJax-Span-181" class="mi">s<sup><span id="MathJax-Span-182" class="texatom"><span id="MathJax-Span-183" class="mrow"><span id="MathJax-Span-184" class="mo">⟨<span id="MathJax-Span-185" class="mi">t<span id="MathJax-Span-186" class="mo">−<span id="MathJax-Span-187" class="mn">1<span id="MathJax-Span-188" class="mo">⟩ 和 <span id="MathJax-Span-190" class="mrow"><span id="MathJax-Span-191" class="msubsup"><span id="MathJax-Span-192" class="mi">a<sup><span id="MathJax-Span-193" class="texatom"><span id="MathJax-Span-194" class="mrow"><span id="MathJax-Span-195" class="mo">⟨<span id="MathJax-Span-196" class="mi">t<span id="MathJax-Span-197" class="mo">⟩以计算 e⟨t,t′⟩, 然后通过 softmax 传递来计算α⟨t,t′⟩。我们将在下面的 Keras中解释如何使用 RepeatVector 和串联。
Lets implement this model. You will start by implementing two functions: one_step_attention() and model().
1) one_step_attention(): At step <span id="MathJax-Span-224" class="mrow"><span id="MathJax-Span-225" class="mi">t, given all the hidden states of the Bi-LSTM (<span id="MathJax-Span-227" class="mrow"><span id="MathJax-Span-228" class="mo">[<span id="MathJax-Span-229" class="msubsup"><span id="MathJax-Span-230" class="mi">a<span id="MathJax-Span-231" class="texatom"><span id="MathJax-Span-232" class="mrow"><span id="MathJax-Span-233" class="mo"><sup><</sup><span id="MathJax-Span-234" class="mn"><sup>1</sup><span id="MathJax-Span-235" class="mo"><sup>></sup><span id="MathJax-Span-236" class="mo">,<span id="MathJax-Span-237" class="msubsup"><span id="MathJax-Span-238" class="mi">a<span id="MathJax-Span-239" class="texatom"><span id="MathJax-Span-240" class="mrow"><span id="MathJax-Span-241" class="mo"><sup><</sup><span id="MathJax-Span-242" class="mn"><sup>2</sup><span id="MathJax-Span-243" class="mo"><sup>></sup><span id="MathJax-Span-244" class="mo">,<span id="MathJax-Span-245" class="mo">.<span id="MathJax-Span-246" class="mo">.<span id="MathJax-Span-247" class="mo">.<span id="MathJax-Span-248" class="mo">,<span id="MathJax-Span-249" class="msubsup"><span id="MathJax-Span-250" class="mi">a<span id="MathJax-Span-251" class="texatom"><span id="MathJax-Span-252" class="mrow"><span id="MathJax-Span-253" class="mo"><sup><</sup><span id="MathJax-Span-254" class="msubsup"><span id="MathJax-Span-255" class="mi"><sup>T</sup><span id="MathJax-Span-256" class="mi"><sub><sup>x</sup></sub><span id="MathJax-Span-257" class="mo"><sup>></sup><span id="MathJax-Span-258" class="mo">]) and the previous hidden state of the second LSTM (<span id="MathJax-Span-260" class="mrow"><span id="MathJax-Span-261" class="msubsup"><span id="MathJax-Span-262" class="mi">s<sup><span id="MathJax-Span-263" class="texatom"><span id="MathJax-Span-264" class="mrow"><span id="MathJax-Span-265" class="mo"><<span id="MathJax-Span-266" class="mi">t<span id="MathJax-Span-267" class="mo">−<span id="MathJax-Span-268" class="mn">1<span id="MathJax-Span-269" class="mo">>), one_step_attention() will compute the attention weights (<span id="MathJax-Span-271" class="mrow"><span id="MathJax-Span-272" class="mo">[<span id="MathJax-Span-273" class="msubsup"><span id="MathJax-Span-274" class="mi">α<span id="MathJax-Span-275" class="texatom"><span id="MathJax-Span-276" class="mrow"><span id="MathJax-Span-277" class="mo"><sup><</sup><span id="MathJax-Span-278" class="mi"><sup>t</sup><span id="MathJax-Span-279" class="mo"><sup>,</sup><span id="MathJax-Span-280" class="mn"><sup>1</sup><span id="MathJax-Span-281" class="mo"><sup>></sup><span id="MathJax-Span-282" class="mo">,<span id="MathJax-Span-283" class="msubsup"><span id="MathJax-Span-284" class="mi">α<span id="MathJax-Span-285" class="texatom"><span id="MathJax-Span-286" class="mrow"><span id="MathJax-Span-287" class="mo"><sup><</sup><span id="MathJax-Span-288" class="mi"><sup>t</sup><span id="MathJax-Span-289" class="mo"><sup>,</sup><span id="MathJax-Span-290" class="mn"><sup>2</sup><span id="MathJax-Span-291" class="mo"><sup>></sup><span id="MathJax-Span-292" class="mo">,<span id="MathJax-Span-293" class="mo">.<span id="MathJax-Span-294" class="mo">.<span id="MathJax-Span-295" class="mo">.<span id="MathJax-Span-296" class="mo">,<span id="MathJax-Span-297" class="msubsup"><span id="MathJax-Span-298" class="mi">α<span id="MathJax-Span-299" class="texatom"><span id="MathJax-Span-300" class="mrow"><span id="MathJax-Span-301" class="mo"><sup><</sup><span id="MathJax-Span-302" class="mi"><sup>t</sup><span id="MathJax-Span-303" class="mo"><sup>,</sup><span id="MathJax-Span-304" class="msubsup"><span id="MathJax-Span-305" class="mi"><sup>T</sup><span id="MathJax-Span-306" class="mi"><sup>x</sup><span id="MathJax-Span-307" class="mo"><sup>></sup><span id="MathJax-Span-308" class="mo">]) and output the context vector (see Figure 1 (right) for details):

Note that we are denoting the attention in this notebook <span id="MathJax-Span-366" class="mrow"><span id="MathJax-Span-367" class="mi">c<span id="MathJax-Span-368" class="mi">o<span id="MathJax-Span-369" class="mi">n<span id="MathJax-Span-370" class="mi">t<span id="MathJax-Span-371" class="mi">e<span id="MathJax-Span-372" class="mi">x<span id="MathJax-Span-373" class="msubsup"><span id="MathJax-Span-374" class="mi">t<sup><span id="MathJax-Span-375" class="texatom"><span id="MathJax-Span-376" class="mrow"><span id="MathJax-Span-377" class="mo">⟨<span id="MathJax-Span-378" class="mi">t<span id="MathJax-Span-379" class="mo">⟩. In the lecture videos, the context was denoted <span id="MathJax-Span-381" class="mrow"><span id="MathJax-Span-382" class="msubsup"><span id="MathJax-Span-383" class="mi">c<sup><span id="MathJax-Span-384" class="texatom"><span id="MathJax-Span-385" class="mrow"><span id="MathJax-Span-386" class="mo">⟨<span id="MathJax-Span-387" class="mi">t<span id="MathJax-Span-388" class="mo">⟩, but here we are calling it <span id="MathJax-Span-390" class="mrow"><span id="MathJax-Span-391" class="mi">c<span id="MathJax-Span-392" class="mi">o<span id="MathJax-Span-393" class="mi">n<span id="MathJax-Span-394" class="mi">t<span id="MathJax-Span-395" class="mi">e<span id="MathJax-Span-396" class="mi">x<span id="MathJax-Span-397" class="msubsup"><span id="MathJax-Span-398" class="mi">t<sup><span id="MathJax-Span-399" class="texatom"><span id="MathJax-Span-400" class="mrow"><span id="MathJax-Span-401" class="mo">⟨<span id="MathJax-Span-402" class="mi">t<span id="MathJax-Span-403" class="mo">⟩ to avoid confusion with the (post-attention) LSTM's internal memory cell variable, which is sometimes also denoted <span id="MathJax-Span-405" class="mrow"><span id="MathJax-Span-406" class="msubsup"><span id="MathJax-Span-407" class="mi">c<sup><span id="MathJax-Span-408" class="texatom"><span id="MathJax-Span-409" class="mrow"><span id="MathJax-Span-410" class="mo">⟨<span id="MathJax-Span-411" class="mi">t<span id="MathJax-Span-412" class="mo">⟩.
2) model(): Implements the entire model. It first runs the input through a Bi-LSTM to get back <span id="MathJax-Span-227" class="mrow"><span id="MathJax-Span-228" class="mo">[<span id="MathJax-Span-229" class="msubsup"><span id="MathJax-Span-230" class="mi">a<span id="MathJax-Span-231" class="texatom"><span id="MathJax-Span-232" class="mrow"><span id="MathJax-Span-233" class="mo"><sup><</sup><span id="MathJax-Span-234" class="mn"><sup>1</sup><span id="MathJax-Span-235" class="mo"><sup>></sup><span id="MathJax-Span-236" class="mo">,<span id="MathJax-Span-237" class="msubsup"><span id="MathJax-Span-238" class="mi">a<span id="MathJax-Span-239" class="texatom"><span id="MathJax-Span-240" class="mrow"><span id="MathJax-Span-241" class="mo"><sup><</sup><span id="MathJax-Span-242" class="mn"><sup>2</sup><span id="MathJax-Span-243" class="mo"><sup>></sup><span id="MathJax-Span-244" class="mo">,<span id="MathJax-Span-245" class="mo">.<span id="MathJax-Span-246" class="mo">.<span id="MathJax-Span-247" class="mo">.<span id="MathJax-Span-248" class="mo">,<span id="MathJax-Span-249" class="msubsup"><span id="MathJax-Span-250" class="mi">a<span id="MathJax-Span-251" class="texatom"><span id="MathJax-Span-252" class="mrow"><span id="MathJax-Span-253" class="mo"><sup><</sup><span id="MathJax-Span-254" class="msubsup"><span id="MathJax-Span-255" class="mi"><sup>T</sup><span id="MathJax-Span-256" class="mi"><sub><sup>x</sup></sub><span id="MathJax-Span-257" class="mo"><sup>></sup><span id="MathJax-Span-258" class="mo">]<span class="MJX_Assistive_MathML">). Then, it calls one_step_attention() <span id="MathJax-Span-447" class="mrow"><span id="MathJax-Span-448" class="msubsup"><span id="MathJax-Span-449" class="mi">T<sub><span id="MathJax-Span-450" class="mi">y times (for loop). At each iteration of this loop, it gives the computed context vector <span id="MathJax-Span-452" class="mrow"><span id="MathJax-Span-453" class="msubsup"><span id="MathJax-Span-454" class="mi">c<sup><span id="MathJax-Span-455" class="texatom"><span id="MathJax-Span-456" class="mrow"><span id="MathJax-Span-457" class="mo"><<span id="MathJax-Span-458" class="mi">t<span id="MathJax-Span-459" class="mo">> to the second LSTM, and runs the output of the LSTM through a dense layer with softmax activation to generate a prediction <span id="MathJax-Span-461" class="mrow"><span id="MathJax-Span-462" class="msubsup"><span id="MathJax-Span-463" class="texatom"><span id="MathJax-Span-464" class="mrow"><span id="MathJax-Span-465" class="munderover"><span id="MathJax-Span-466" class="mi">y<span id="MathJax-Span-467" class="mo">̂ <sup><span id="MathJax-Span-468" class="texatom"><span id="MathJax-Span-469" class="mrow"><span id="MathJax-Span-470" class="mo"><<span id="MathJax-Span-471" class="mi">t<span id="MathJax-Span-472" class="mo">>.
【中文翻译】
让我们实现这个模型。您将首先实现两个函数: one_step_attention() 和 model()。
1) one_step_attention (): 在步骤 t 中, 考虑到 the Bi-LSTM的所有隐藏状态 (<span id="MathJax-Span-227" class="mrow"><span id="MathJax-Span-228" class="mo">[<span id="MathJax-Span-229" class="msubsup"><span id="MathJax-Span-230" class="mi">a<span id="MathJax-Span-231" class="texatom"><span id="MathJax-Span-232" class="mrow"><span id="MathJax-Span-233" class="mo"><sup><</sup><span id="MathJax-Span-234" class="mn"><sup>1</sup><span id="MathJax-Span-235" class="mo"><sup>></sup><span id="MathJax-Span-236" class="mo">,<span id="MathJax-Span-237" class="msubsup"><span id="MathJax-Span-238" class="mi">a<span id="MathJax-Span-239" class="texatom"><span id="MathJax-Span-240" class="mrow"><span id="MathJax-Span-241" class="mo"><sup><</sup><span id="MathJax-Span-242" class="mn"><sup>2</sup><span id="MathJax-Span-243" class="mo"><sup>></sup><span id="MathJax-Span-244" class="mo">,<span id="MathJax-Span-245" class="mo">.<span id="MathJax-Span-246" class="mo">.<span id="MathJax-Span-247" class="mo">.<span id="MathJax-Span-248" class="mo">,<span id="MathJax-Span-249" class="msubsup"><span id="MathJax-Span-250" class="mi">a<span id="MathJax-Span-251" class="texatom"><span id="MathJax-Span-252" class="mrow"><span id="MathJax-Span-253" class="mo"><sup><</sup><span id="MathJax-Span-254" class="msubsup"><span id="MathJax-Span-255" class="mi"><sup>T</sup><span id="MathJax-Span-256" class="mi"><sub><sup>x</sup></sub><span id="MathJax-Span-257" class="mo"><sup>></sup><span id="MathJax-Span-258" class="mo">]<span class="MJX_Assistive_MathML">)以及第二个 LSTM (s) 的前一个隐藏状态(<span id="MathJax-Span-260" class="mrow"><span id="MathJax-Span-261" class="msubsup"><span id="MathJax-Span-262" class="mi">s<sup><span id="MathJax-Span-263" class="texatom"><span id="MathJax-Span-264" class="mrow"><span id="MathJax-Span-265" class="mo"><<span id="MathJax-Span-266" class="mi">t<span id="MathJax-Span-267" class="mo">−<span id="MathJax-Span-268" class="mn">1<span id="MathJax-Span-269" class="mo">>), one_step_attention () 将计算attention weights(<span id="MathJax-Span-271" class="mrow"><span id="MathJax-Span-272" class="mo">[<span id="MathJax-Span-273" class="msubsup"><span id="MathJax-Span-274" class="mi">α<span id="MathJax-Span-275" class="texatom"><span id="MathJax-Span-276" class="mrow"><span id="MathJax-Span-277" class="mo"><sup><</sup><span id="MathJax-Span-278" class="mi"><sup>t</sup><span id="MathJax-Span-279" class="mo"><sup>,</sup><span id="MathJax-Span-280" class="mn"><sup>1</sup><span id="MathJax-Span-281" class="mo"><sup>></sup><span id="MathJax-Span-282" class="mo">,<span id="MathJax-Span-283" class="msubsup"><span id="MathJax-Span-284" class="mi">α<span id="MathJax-Span-285" class="texatom"><span id="MathJax-Span-286" class="mrow"><span id="MathJax-Span-287" class="mo"><sup><</sup><span id="MathJax-Span-288" class="mi"><sup>t</sup><span id="MathJax-Span-289" class="mo"><sup>,</sup><span id="MathJax-Span-290" class="mn"><sup>2</sup><span id="MathJax-Span-291" class="mo"><sup>></sup><span id="MathJax-Span-292" class="mo">,<span id="MathJax-Span-293" class="mo">.<span id="MathJax-Span-294" class="mo">.<span id="MathJax-Span-295" class="mo">.<span id="MathJax-Span-296" class="mo">,<span id="MathJax-Span-297" class="msubsup"><span id="MathJax-Span-298" class="mi">α<span id="MathJax-Span-299" class="texatom"><span id="MathJax-Span-300" class="mrow"><span id="MathJax-Span-301" class="mo"><sup><</sup><span id="MathJax-Span-302" class="mi"><sup>t</sup><span id="MathJax-Span-303" class="mo"><sup>,</sup><span id="MathJax-Span-304" class="msubsup"><span id="MathJax-Span-305" class="mi"><sup>T</sup><span id="MathJax-Span-306" class="mi"><sup>x</sup><span id="MathJax-Span-307" class="mo"><sup>></sup><span id="MathJax-Span-308" class="mo">]<span class="MJX_Assistive_MathML">)和输出the context vector (请参见图 1 (右) 以了解详细信息):

注意, 我们在这本笔记本中用context⟨t⟩ 表示the attention。在讲座视频中, the context被表示为 c⟨t⟩, 但在这里我们称之为 context⟨t⟩, 以避免混淆 (post-attention) LSTM 的内部内存单元格变量, 这有时也被表示为 c⟨t⟩。
2) model(): 实现整个模型。它首先通过Bi-LSTM 运行输入以返回[a<1>,a<2>,...,a<Tx>])。然后, 它调用one_step_attention() Ty次。(for 循环)。在该循环的每个迭代中, 它将计算context vector <span id="MathJax-Span-452" class="mrow"><span id="MathJax-Span-453" class="msubsup"><span id="MathJax-Span-454" class="mi">c<sup><span id="MathJax-Span-455" class="texatom"><span id="MathJax-Span-456" class="mrow"><span id="MathJax-Span-457" class="mo"><<span id="MathJax-Span-458" class="mi">t<span id="MathJax-Span-459" class="mo">>,赋予第二个 LSTM, 并通过具有 softmax 激活的dense层运行 LSTM 的输出, 以生成预测ŷ <t>.
Exercise: Implement one_step_attention(). The function model() will call the layers in one_step_attention() <span id="MathJax-Span-474" class="mrow"><span id="MathJax-Span-475" class="msubsup"><span id="MathJax-Span-476" class="mi">T<sub><span id="MathJax-Span-477" class="mi">y using a for-loop, and it is important that all <span id="MathJax-Span-479" class="mrow"><span id="MathJax-Span-480" class="msubsup"><span id="MathJax-Span-481" class="mi">T<sub><span id="MathJax-Span-482" class="mi">y copies have the same weights. I.e., it should not re-initiaiize the weights every time. In other words, all <span id="MathJax-Span-484" class="mrow"><span id="MathJax-Span-485" class="msubsup"><span id="MathJax-Span-486" class="mi">T<sub><span id="MathJax-Span-487" class="mi">y steps should have shared weights. Here's how you can implement layers with shareable weights in Keras:
- Define the layer objects (as global variables for examples).
- Call these objects when propagating the input.
We have defined the layers you need as global variables. Please run the following cells to create them. Please check the Keras documentation to make sure you understand what these layers are: RepeatVector(), Concatenate(), Dense(), Activation(), Dot().
【中文翻译】
练习: 实施 one_step_attention ()。函数 model() 将使用 for 循环调用 one_step_attention ()Ty 次, 并且所有的 Ty 拷贝都具有相同的权重是很重要的。也就是说, 它不应该每次重新初始化。换言之, 所有的 Ty 步骤都应该具有共享权重。下面是如何在 Keras 中实现可共享权重的层:
1.定义层对象 (作为示例的全局变量)。
2.传播输入时调用这些对象。
我们已将需要的层定义为全局变量。请运行以下单元格以创建它们。请检查 Keras 文档, 以确保了解这些图层的容: RepeatVector(), Concatenate(), Dense(), Activation(), Dot().
【code】
# Defined shared layers as global variablesrepeator = RepeatVector(Tx)concatenator = Concatenate(axis=-1)densor1 = Dense(10, activation = "tanh")densor2 = Dense(1, activation = "relu")activator = Activation(softmax, name='attention_weights') # We are using a custom softmax(axis = 1) loaded in this notebookdotor = Dot(axes = 1) |
Now you can use these layers to implement one_step_attention(). In order to propagate a Keras tensor object X through one of these layers, use layer(X) (or layer([X,Y]) if it requires multiple inputs.), e.g. densor(X) will propagate X through the Dense(1) layer defined above.
【code】
# GRADED FUNCTION: one_step_attentiondef one_step_attention(a, s_prev): """ Performs one step of attention: Outputs a context vector computed as a dot product of the attention weights "alphas" and the hidden states "a" of the Bi-LSTM. Arguments: a -- hidden state output of the Bi-LSTM, numpy-array of shape (m, Tx, 2*n_a) s_prev -- previous hidden state of the (post-attention) LSTM, numpy-array of shape (m, n_s) Returns: context -- context vector, input of the next (post-attetion) LSTM cell """ ### START CODE HERE ### # Use repeator to repeat s_prev to be of shape (m, Tx, n_s) so that you can concatenate it with all hidden states "a" (≈ 1 line) s_prev = repeator(s_prev) # Use concatenator to concatenate a and s_prev on the last axis (≈ 1 line) concat = concatenator([a,s_prev]) # Use densor1 to propagate concat through a small fully-connected neural network to compute the "intermediate energies" variable e. (≈1 lines) e = densor1(concat) # Use densor2 to propagate e through a small fully-connected neural network to compute the "energies" variable energies. (≈1 lines) energies = densor2(e) # Use "activator" on "energies" to compute the attention weights "alphas" (≈ 1 line) alphas = activator(energies) # Use dotor together with "alphas" and "a" to compute the context vector to be given to the next (post-attention) LSTM-cell (≈ 1 line) context = dotor([ alphas,a]) ### END CODE HERE ### return context |
You will be able to check the expected output of one_step_attention() after you've coded the model() function.
Exercise: Implement model() as explained in figure 2 and the text above. Again, we have defined global layers that will share weights to be used in model().
【code】
n_a = 32n_s = 64post_activation_LSTM_cell = LSTM(n_s, return_state = True)output_layer = Dense(len(machine_vocab), activation=softmax) |
Now you can use these layers Ty times in a for loop to generate the outputs, and their parameters will not be reinitialized. You will have to carry out the following steps:
- Propagate the input into a Bidirectional LSTM
-
Iterate for t=0,…,Ty−1:
- Call
one_step_attention()on [α<t,1>,α<t,2>,...,α<t,Tx>] and s<t−1> to get the context vector context<t>. - Give context<t> to the post-attention LSTM cell. Remember pass in the previous hidden-state s⟨t−1⟩ and cell-states c⟨t−1⟩ of this LSTM using
initial_state= [previous hidden state, previous cell state]. Get back the new hidden state s<t> and the new cell state c<t>. - Apply a softmax layer to s<t>, get the output.
- Save the output by adding it to the list of outputs.
- Call
-
Create your Keras model instance, it should have three inputs ("inputs", s<0> and c<0>) and output the list of "outputs".
【code】
# GRADED FUNCTION: modeldef model(Tx, Ty, n_a, n_s, human_vocab_size, machine_vocab_size): """ Arguments: Tx -- length of the input sequence Ty -- length of the output sequence n_a -- hidden state size of the Bi-LSTM n_s -- hidden state size of the post-attention LSTM human_vocab_size -- size of the python dictionary "human_vocab" machine_vocab_size -- size of the python dictionary "machine_vocab" Returns: model -- Keras model instance """ # Define the inputs of your model with a shape (Tx,) # Define s0 and c0, initial hidden state for the decoder LSTM of shape (n_s,) X = Input(shape=(Tx, human_vocab_size)) s0 = Input(shape=(n_s,), name='s0') c0 = Input(shape=(n_s,), name='c0') s = s0 c = c0 # Initialize empty list of outputs outputs = [] ### START CODE HERE ### # Step 1: Define your pre-attention Bi-LSTM. Remember to use return_sequences=True. (≈ 1 line) a = Bidirectional(LSTM(n_a, return_sequences = True), input_shape = (m, Tx, n_a*2))(X) # Step 2: Iterate for Ty steps for t in range(Ty): # Step 2.A: Perform one step of the attention mechanism to get back the context vector at step t (≈ 1 line) context = one_step_attention(a, s) # Step 2.B: Apply the post-attention LSTM cell to the "context" vector. # Don't forget to pass: initial_state = [hidden state, cell state] (≈ 1 line) s, _, c = post_activation_LSTM_cell(context,initial_state = [s, c]) # Step 2.C: Apply Dense layer to the hidden state output of the post-attention LSTM (≈ 1 line) out = output_layer(s) # Step 2.D: Append "out" to the "outputs" list (≈ 1 line) outputs.append(out) # Step 3: Create model instance taking three inputs and returning the list of outputs. (≈ 1 line) model = Model([X, s0, c0], outputs = outputs) ### END CODE HERE ### return model |
Run the following cell to create your model.
【code】
model = model(Tx, Ty, n_a, n_s, len(human_vocab), len(machine_vocab)) |
Let's get a summary of the model to check if it matches the expected output.
【code】
model.summary() |
【result】
____________________________________________________________________________________________________Layer (type) Output Shape Param # Connected to ====================================================================================================input_6 (InputLayer) (None, 30, 37) 0 ____________________________________________________________________________________________________s0 (InputLayer) (None, 64) 0 ____________________________________________________________________________________________________bidirectional_6 (Bidirectional) (None, 30, 64) 17920 input_6[0][0] ____________________________________________________________________________________________________repeat_vector_1 (RepeatVector) (None, 30, 64) 0 s0[0][0] lstm_9[0][0] lstm_9[1][0] lstm_9[2][0] lstm_9[3][0] lstm_9[4][0] lstm_9[5][0] lstm_9[6][0] lstm_9[7][0] lstm_9[8][0] ____________________________________________________________________________________________________concatenate_1 (Concatenate) (None, 30, 128) 0 bidirectional_6[0][0] repeat_vector_1[2][0] bidirectional_6[0][0] repeat_vector_1[3][0] bidirectional_6[0][0] repeat_vector_1[4][0] bidirectional_6[0][0] repeat_vector_1[5][0] bidirectional_6[0][0] repeat_vector_1[6][0] bidirectional_6[0][0] repeat_vector_1[7][0] bidirectional_6[0][0] repeat_vector_1[8][0] bidirectional_6[0][0] repeat_vector_1[9][0] bidirectional_6[0][0] repeat_vector_1[10][0] bidirectional_6[0][0] repeat_vector_1[11][0] ____________________________________________________________________________________________________dense_1 (Dense) (None, 30, 10) 1290 concatenate_1[0][0] concatenate_1[1][0] concatenate_1[2][0] concatenate_1[3][0] concatenate_1[4][0] concatenate_1[5][0] concatenate_1[6][0] concatenate_1[7][0] concatenate_1[8][0] concatenate_1[9][0] ____________________________________________________________________________________________________dense_2 (Dense) (None, 30, 1) 11 dense_1[0][0] dense_1[1][0] dense_1[2][0] dense_1[3][0] dense_1[4][0] dense_1[5][0] dense_1[6][0] dense_1[7][0] dense_1[8][0] dense_1[9][0] ____________________________________________________________________________________________________attention_weights (Activation) (None, 30, 1) 0 dense_2[0][0] dense_2[1][0] dense_2[2][0] dense_2[3][0] dense_2[4][0] dense_2[5][0] dense_2[6][0] dense_2[7][0] dense_2[8][0] dense_2[9][0] ____________________________________________________________________________________________________dot_1 (Dot) (None, 1, 64) 0 attention_weights[0][0] bidirectional_6[0][0] attention_weights[1][0] bidirectional_6[0][0] attention_weights[2][0] bidirectional_6[0][0] attention_weights[3][0] bidirectional_6[0][0] attention_weights[4][0] bidirectional_6[0][0] attention_weights[5][0] bidirectional_6[0][0] attention_weights[6][0] bidirectional_6[0][0] attention_weights[7][0] bidirectional_6[0][0] attention_weights[8][0] bidirectional_6[0][0] attention_weights[9][0] bidirectional_6[0][0] ____________________________________________________________________________________________________c0 (InputLayer) (None, 64) 0 ____________________________________________________________________________________________________lstm_9 (LSTM) [(None, 64), (None, 6 33024 dot_1[0][0] s0[0][0] c0[0][0] dot_1[1][0] lstm_9[0][0] lstm_9[0][2] dot_1[2][0] lstm_9[1][0] lstm_9[1][2] dot_1[3][0] lstm_9[2][0] lstm_9[2][2] dot_1[4][0] lstm_9[3][0] lstm_9[3][2] dot_1[5][0] lstm_9[4][0] lstm_9[4][2] dot_1[6][0] lstm_9[5][0] lstm_9[5][2] dot_1[7][0] lstm_9[6][0] lstm_9[6][2] dot_1[8][0] lstm_9[7][0] lstm_9[7][2] dot_1[9][0] lstm_9[8][0] lstm_9[8][2] ____________________________________________________________________________________________________dense_6 (Dense) (None, 11) 715 lstm_9[0][0] lstm_9[1][0] lstm_9[2][0] lstm_9[3][0] lstm_9[4][0] lstm_9[5][0] lstm_9[6][0] lstm_9[7][0] lstm_9[8][0] lstm_9[9][0] ====================================================================================================Total params: 52,960Trainable params: 52,960Non-trainable params: 0____________________________________________________________________________________________________ |
【Expected Output】
Here is the summary you should see
Total params: 52,960Trainable params: 52,960Non-trainable params: 0bidirectional_1's output shape (None, 30, 64)repeat_vector_1's output shape (None, 30, 64)concatenate_1's output shape (None, 30, 128)attention_weights's output shape (None, 30, 1)dot_1's output shape (None, 1, 64)dense_3's output shape (None, 11) |
As usual, after creating your model in Keras, you need to compile it and define what loss, optimizer and metrics your are want to use. Compile your model using categorical_crossentropy loss, a custom Adam optimizer (learning rate = 0.005, <span id="MathJax-Span-654" class="mrow"><span id="MathJax-Span-655" class="msubsup"><span id="MathJax-Span-656" class="mi">β<span id="MathJax-Span-657" class="mn"><sub>1</sub><span id="MathJax-Span-658" class="mo">=<span id="MathJax-Span-659" class="mn">0.9, <span id="MathJax-Span-661" class="mrow"><span id="MathJax-Span-662" class="msubsup"><span id="MathJax-Span-663" class="mi">β<span id="MathJax-Span-664" class="mn"><sub>2</sub><span id="MathJax-Span-665" class="mo">=<span id="MathJax-Span-666" class="mn">0.999, decay = 0.01) and ['accuracy'] metrics:
【code】
### START CODE HERE ### (≈2 lines)opt = Adam(lr = 0.005, beta_1 = 0.9, beta_2 = 0.999,decay = 0.01) model.compile(loss = 'categorical_crossentropy', optimizer = opt,metrics = ['accuracy']) ### END CODE HERE ### |
The last step is to define all your inputs and outputs to fit the model:
- You already have X of shape <span id="MathJax-Span-668" class="mrow"><span id="MathJax-Span-669" class="mo">(<span id="MathJax-Span-670" class="mi">m<span id="MathJax-Span-671" class="mo">=<span id="MathJax-Span-672" class="mn">10000<span id="MathJax-Span-673" class="mo">,<span id="MathJax-Span-674" class="msubsup"><span id="MathJax-Span-675" class="mi">T<span id="MathJax-Span-676" class="mi"><sub>x</sub><span id="MathJax-Span-677" class="mo">=<span id="MathJax-Span-678" class="mn">30<span id="MathJax-Span-679" class="mo">) containing the training examples.
- You need to create
s0andc0to initialize yourpost_activation_LSTM_cellwith 0s. - Given the
model()you coded, you need the "outputs" to be a list of 11 elements of shape (m, T_y). So that:outputs[i][0], ..., outputs[i][Ty]represent the true labels (characters) corresponding to the <span id="MathJax-Span-681" class="mrow"><span id="MathJax-Span-682" class="msubsup"><span id="MathJax-Span-683" class="mi">i<span id="MathJax-Span-684" class="texatom"><span id="MathJax-Span-685" class="mrow"><span id="MathJax-Span-686" class="mi">t<span id="MathJax-Span-687" class="mi">hith training example (X[i]). More generally,outputs[i][j]is the true label of the <span id="MathJax-Span-689" class="mrow"><span id="MathJax-Span-690" class="msubsup"><span id="MathJax-Span-691" class="mi">j<sup><span id="MathJax-Span-692" class="texatom"><span id="MathJax-Span-693" class="mrow"><span id="MathJax-Span-694" class="mi">t<span id="MathJax-Span-695" class="mi">h character in the <span id="MathJax-Span-697" class="mrow"><span id="MathJax-Span-698" class="msubsup"><span id="MathJax-Span-699" class="mi">i<span id="MathJax-Span-700" class="texatom"><span id="MathJax-Span-701" class="mrow"><span id="MathJax-Span-702" class="mi">t<span id="MathJax-Span-703" class="mi">hithtraining example.
【code】
s0 = np.zeros((m, n_s))c0 = np.zeros((m, n_s))outputs = list(Yoh.swapaxes(0,1)) |
Let's now fit the model and run it for one epoch.
【code】
model.fit([Xoh, s0, c0], outputs, epochs=1, batch_size=100) |
【result】
Epoch 1/110000/10000 [==============================] - 46s - loss: 16.5956 - dense_6_loss_1: 1.2932 - dense_6_loss_2: 1.0162 - dense_6_loss_3: 1.7596 - dense_6_loss_4: 2.6613 <br>- dense_6_loss_5: 0.7426 - dense_6_loss_6: 1.3393 - dense_6_loss_7: 2.6329 - dense_6_loss_8: 0.8744 - dense_6_loss_9: 1.7038 - dense_6_loss_10: 2.5724 <br>- dense_6_acc_1: 0.4418 - dense_6_acc_2: 0.6646 - dense_6_acc_3: 0.2957 - dense_6_acc_4: 0.0854 - dense_6_acc_5: 0.9590 - dense_6_acc_6: 0.3268 <br>- dense_6_acc_7: 0.0647 - dense_6_acc_8: 0.9349 - dense_6_acc_9: 0.2069 - dense_6_acc_10: 0.1007 <keras.callbacks.History at 0x7fdd32eb9b38> |
While training you can see the loss as well as the accuracy on each of the 10 positions of the output. The table below gives you an example of what the accuracies could be if the batch had 2 examples:
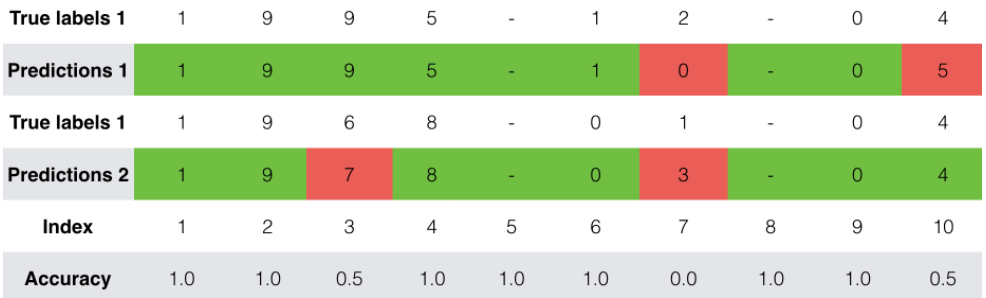
Thus, dense_2_acc_8: 0.89 means that you are predicting the 7th character of the output correctly 89% of the time in the current batch of data.
We have run this model for longer, and saved the weights. Run the next cell to load our weights. (By training a model for several minutes, you should be able to obtain a model of similar accuracy, but loading our model will save you time.)
【code】
model.load_weights('models/model.h5') |
You can now see the results on new examples.
【code】
EXAMPLES = ['3 May 1979', '5 April 09', '21th of August 2016', 'Tue 10 Jul 2007', 'Saturday May 9 2018', 'March 3 2001', 'March 3rd 2001', '1 March 2001']for example in EXAMPLES: source = string_to_int(example, Tx, human_vocab) source = np.array(list(map(lambda x: to_categorical(x, num_classes=len(human_vocab)), source))).swapaxes(0,1) prediction = model.predict([source, s0, c0]) prediction = np.argmax(prediction, axis = -1) output = [inv_machine_vocab[int(i)] for i in prediction] print("source:", example) print("output:", ''.join(output)) |
【result】
source: 3 May 1979output: 1977-07-07source: 5 April 09output: 1975-05-07source: 21th of August 2016output: 2000-05-05source: Tue 10 Jul 2007output: 2000-00-20source: Saturday May 9 2018output: 1905-02-05source: March 3 2001output: 2000-05-20source: March 3rd 2001output: 2000-00-20source: 1 March 2001output: 2000-00-20 |
You can also change these examples to test with your own examples. The next part will give you a better sense on what the attention mechanism is doing--i.e., what part of the input the network is paying attention to when generating a particular output character.
3 - Visualizing Attention (Optional / Ungraded)
Since the problem has a fixed output length of 10, it is also possible to carry out this task using 10 different softmax units to generate the 10 characters of the output. But one advantage of the attention model is that each part of the output (say the month) knows it needs to depend only on a small part of the input (the characters in the input giving the month). We can visualize what part of the output is looking at what part of the input.
【中文翻译】
由于该问题具有固定的输出长度 10, 因此可以使用10个不同的 softmax 单元来执行此任务, 以生成输出的10个字符。但注意模型的一个优点是, 输出的每个部分 (比如月份) 都知道它只需要依赖输入的一小部分 (输入月份的字符)。我们可以可视化输出的哪一部分正在查看输入的哪一部分。
Consider the task of translating "Saturday 9 May 2018" to "2018-05-09". If we visualize the computed <span id="MathJax-Span-705" class="mrow"><span id="MathJax-Span-706" class="msubsup"><span id="MathJax-Span-707" class="mi">α<span id="MathJax-Span-708" class="texatom"><span id="MathJax-Span-709" class="mrow"><span id="MathJax-Span-710" class="mo"><sup>⟨</sup><span id="MathJax-Span-711" class="mi"><sup>t</sup><span id="MathJax-Span-712" class="mo"><sup>,</sup><span id="MathJax-Span-713" class="msup"><span id="MathJax-Span-714" class="mi"><sup>t</sup><span id="MathJax-Span-715" class="mo"><sup>′</sup><span id="MathJax-Span-716" class="mo"><sup>⟩</sup> we get this:

Notice how the output ignores the "Saturday" portion of the input. None of the output timesteps are paying much attention to that portion of the input. We see also that 9 has been translated as 09 and May has been correctly translated into 05, with the output paying attention to the parts of the input it needs to to make the translation. The year mostly requires it to pay attention to the input's "18" in order to generate "2018."
【中文翻译】
注意输出如何忽略输入的 "Saturday " 部分。所有输出 时间步都不太注意输入的那一部分。我们还看到, 9 已被翻译为 09, 并May已正确翻译成 05。年份需要它注意输入的 "18 " 才能生成 "2018"。
3.1 - Getting the activations from the network
Lets now visualize the attention values in your network. We'll propagate an example through the network, then visualize the values of <span id="MathJax-Span-718" class="mrow"><span id="MathJax-Span-719" class="msubsup"><span id="MathJax-Span-720" class="mi">α<sup><span id="MathJax-Span-721" class="texatom"><span id="MathJax-Span-722" class="mrow"><span id="MathJax-Span-723" class="mo">⟨<span id="MathJax-Span-724" class="mi">t<span id="MathJax-Span-725" class="mo">,<span id="MathJax-Span-726" class="msup"><span id="MathJax-Span-727" class="mi">t<span id="MathJax-Span-728" class="mo">′<span id="MathJax-Span-729" class="mo">⟩.
To figure out where the attention values are located, let's start by printing a summary of the model .
【code】
model.summary() |
【result】
___________________________________________________________________________________________________Layer (type) Output Shape Param # Connected to ====================================================================================================input_6 (InputLayer) (None, 30, 37) 0 ____________________________________________________________________________________________________s0 (InputLayer) (None, 64) 0 ____________________________________________________________________________________________________bidirectional_6 (Bidirectional) (None, 30, 64) 17920 input_6[0][0] ____________________________________________________________________________________________________repeat_vector_1 (RepeatVector) (None, 30, 64) 0 s0[0][0] lstm_9[0][0] lstm_9[1][0] lstm_9[2][0] lstm_9[3][0] lstm_9[4][0] lstm_9[5][0] lstm_9[6][0] lstm_9[7][0] lstm_9[8][0] ____________________________________________________________________________________________________concatenate_1 (Concatenate) (None, 30, 128) 0 bidirectional_6[0][0] repeat_vector_1[2][0] bidirectional_6[0][0] repeat_vector_1[3][0] bidirectional_6[0][0] repeat_vector_1[4][0] bidirectional_6[0][0] repeat_vector_1[5][0] bidirectional_6[0][0] repeat_vector_1[6][0] bidirectional_6[0][0] repeat_vector_1[7][0] bidirectional_6[0][0] repeat_vector_1[8][0] bidirectional_6[0][0] repeat_vector_1[9][0] bidirectional_6[0][0] repeat_vector_1[10][0] bidirectional_6[0][0] repeat_vector_1[11][0] ____________________________________________________________________________________________________dense_1 (Dense) (None, 30, 10) 1290 concatenate_1[0][0] concatenate_1[1][0] concatenate_1[2][0] concatenate_1[3][0] concatenate_1[4][0] concatenate_1[5][0] concatenate_1[6][0] concatenate_1[7][0] concatenate_1[8][0] concatenate_1[9][0] ____________________________________________________________________________________________________dense_2 (Dense) (None, 30, 1) 11 dense_1[0][0] dense_1[1][0] dense_1[2][0] dense_1[3][0] dense_1[4][0] dense_1[5][0] dense_1[6][0] dense_1[7][0] dense_1[8][0] dense_1[9][0] ____________________________________________________________________________________________________attention_weights (Activation) (None, 30, 1) 0 dense_2[0][0] dense_2[1][0] dense_2[2][0] dense_2[3][0] dense_2[4][0] dense_2[5][0] dense_2[6][0] dense_2[7][0] dense_2[8][0] dense_2[9][0] ____________________________________________________________________________________________________dot_1 (Dot) (None, 1, 64) 0 attention_weights[0][0] bidirectional_6[0][0] attention_weights[1][0] bidirectional_6[0][0] attention_weights[2][0] bidirectional_6[0][0] attention_weights[3][0] bidirectional_6[0][0] attention_weights[4][0] bidirectional_6[0][0] attention_weights[5][0] bidirectional_6[0][0] attention_weights[6][0] bidirectional_6[0][0] attention_weights[7][0] bidirectional_6[0][0] attention_weights[8][0] bidirectional_6[0][0] attention_weights[9][0] bidirectional_6[0][0] ____________________________________________________________________________________________________c0 (InputLayer) (None, 64) 0 ____________________________________________________________________________________________________lstm_9 (LSTM) [(None, 64), (None, 6 33024 dot_1[0][0] s0[0][0] c0[0][0] dot_1[1][0] lstm_9[0][0] lstm_9[0][2] dot_1[2][0] lstm_9[1][0] lstm_9[1][2] dot_1[3][0] lstm_9[2][0] lstm_9[2][2] dot_1[4][0] lstm_9[3][0] lstm_9[3][2] dot_1[5][0] lstm_9[4][0] lstm_9[4][2] dot_1[6][0] lstm_9[5][0] lstm_9[5][2] dot_1[7][0] lstm_9[6][0] lstm_9[6][2] dot_1[8][0] lstm_9[7][0] lstm_9[7][2] dot_1[9][0] lstm_9[8][0] lstm_9[8][2] ____________________________________________________________________________________________________dense_6 (Dense) (None, 11) 715 lstm_9[0][0] lstm_9[1][0] lstm_9[2][0] lstm_9[3][0] lstm_9[4][0] lstm_9[5][0] lstm_9[6][0] lstm_9[7][0] lstm_9[8][0] lstm_9[9][0] ====================================================================================================Total params: 52,960Trainable params: 52,960Non-trainable params: 0____________________________________________________________________________________________________ |
Navigate through the output of model.summary() above. You can see that the layer named attention_weights outputs the alphas of shape (m, 30, 1) before dot_2 computes the context vector for every time step <span id="MathJax-Span-731" class="mrow"><span id="MathJax-Span-732" class="mi">t<span id="MathJax-Span-733" class="mo">=<span id="MathJax-Span-734" class="mn">0<span id="MathJax-Span-735" class="mo">,<span id="MathJax-Span-736" class="mo">…<span id="MathJax-Span-737" class="mo">,<span id="MathJax-Span-738" class="msubsup"><span id="MathJax-Span-739" class="mi">T<span id="MathJax-Span-740" class="mi"><sub>y</sub><span id="MathJax-Span-741" class="mo">−<span id="MathJax-Span-742" class="mn">1. Lets get the activations from this layer.
【中文翻译】
在 model.summary()的输出中导航。您可以看到名为 attention_weights 的层在 dot_1 计算每个时间步骤 t=0,..., Ty−1的上下文向量之前, 输出形状为 (m、30、1)的alphas。让我们从这个层得到激活。
The function attention_map() pulls out the attention values from your model and plots them.
【code】
attention_map = plot_attention_map(model, human_vocab, inv_machine_vocab, "Tuesday 09 Oct 1993", num = 7, n_s = 64) |
【result】

On the generated plot you can observe the values of the attention weights for each character of the predicted output. Examine this plot and check that where the network is paying attention makes sense to you.
In the date translation application, you will observe that most of the time attention helps predict the year, and hasn't much impact on predicting the day/month.
【中文翻译】
在生成的图形上, 您可以观察预测输出的每个字符的注意权重值。检查这个情节并检查网络关注的地方是否对你有意义。
在日期翻译应用程序中, 您将观察到大多数时间的关注有助于预测年份, 并且对预测日/月没有太大影响。
Congratulations!
You have come to the end of this assignment
Here's what you should remember from this notebook:
- Machine translation models can be used to map from one sequence to another. They are useful not just for translating human languages (like French->English) but also for tasks like date format translation.
- An attention mechanism allows a network to focus on the most relevant parts of the input when producing a specific part of the output.
- A network using an attention mechanism can translate from inputs of length <span id="MathJax-Span-744" class="mrow"><span id="MathJax-Span-745" class="msubsup"><span id="MathJax-Span-746" class="mi">T<sub><span id="MathJax-Span-747" class="mi">x to outputs of length <span id="MathJax-Span-749" class="mrow"><span id="MathJax-Span-750" class="msubsup"><span id="MathJax-Span-751" class="mi">T<sub><span id="MathJax-Span-752" class="mi">y , where <span id="MathJax-Span-754" class="mrow"><span id="MathJax-Span-755" class="msubsup"><span id="MathJax-Span-756" class="mi">T<sub><span id="MathJax-Span-757" class="mi">x and <span id="MathJax-Span-759" class="mrow"><span id="MathJax-Span-760" class="msubsup"><span id="MathJax-Span-761" class="mi">T<sub><span id="MathJax-Span-762" class="mi">y can be different.
- You can visualize attention weights <span id="MathJax-Span-764" class="mrow"><span id="MathJax-Span-765" class="msubsup"><span id="MathJax-Span-766" class="mi">α<sup><span id="MathJax-Span-767" class="texatom"><span id="MathJax-Span-768" class="mrow"><span id="MathJax-Span-769" class="mo">⟨<span id="MathJax-Span-770" class="mi">t<span id="MathJax-Span-771" class="mo">,<span id="MathJax-Span-772" class="msup"><span id="MathJax-Span-773" class="mi">t<span id="MathJax-Span-774" class="mo">′<span id="MathJax-Span-775" class="mo">⟩ to see what the network is paying attention to while generating each output.
Congratulations on finishing this assignment! You are now able to implement an attention model and use it to learn complex mappings from one sequence to another.
【中文翻译】
祝贺!
你已经完成了这个任务!
以下是您在本笔记本中应该记住的内容:
机器翻译模型可用于从一个序列映射到另一个序列。它们不仅用于翻译人类语言 (如法语-英语), 而且对于诸如日期格式翻译之类的任务也很有用。
注意机制允许网络在生成特定部分输出时, 将焦点放在输入的最相关部分。
使用注意机制的网络可以从长度 Tx 的输入转换为长度 Ty 的输出, 在那里Tx 和 Ty 可以不同。
您可以可视化注意权重α⟨t, t′⟩,在生成每个输出时查看网络所关注的内容。
恭喜你完成了任务!现在, 您可以实现一个注意模型, 并使用学习复杂映射,它从一个序列映射到另一个序列。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!