剑指offer二十三之二叉搜索树的后序遍历序列
一、题目
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
二、思路
1、二叉搜索树又称二叉排序树(Binary Sort Tree)或二叉查找树(Binary Search Tree)。二叉搜索树或者是一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
(3)左、右子树也分别为二叉搜索树。
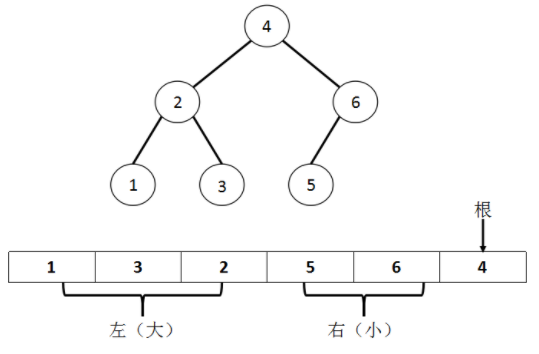
2、对于后序遍历来说,序列数组的最后一个元素一定是根节点, 则根据这个元素,将前面的数组分为左、右两个部分,左侧部分都小,右侧部分都大,如果右侧部分有比该根节点小的元素,那么就不是后序遍历,如此递归进行。
三、代码

public boolean VerifySquenceOfBST(int[] sequence) { if (sequence == null || sequence.length == 0) { return false; } boolean flag = isBST(sequence, 0, sequence.length - 1); return flag; } public boolean isBST(int[] arr, int start, int end) { //所有子序列都检验完成,没有错,返回true if (start>= end) { return true; } // 当前数组(从start到end部分)的根节点 int curElement = arr[end]; int splitIndex; // 找到比curElement大和比curElement小的分界点,分成左侧、右侧两组数据 for (splitIndex = start; splitIndex < end && arr[splitIndex] < curElement; splitIndex++) ; // 只需要看右侧即可,因为前面的for循环,已经确保左侧部分全部都小于curElement for (int i = splitIndex; i < end; i++) { if (arr[i] < curElement) { return false; } } return isBST(arr, start, splitIndex - 1) && isBST(arr, splitIndex, end - 1); }
-----------------------------------------------------------------------------------
参考链接:https://www.nowcoder.com/questionTerminal/a861533d45854474ac791d90e447bafd




