离散序列的标准互信息计算(转载)

                                                                                                    离散序列的标准互信息计算

                                                                来源：http://www.cnblogs.com/ziqiao/archive/2011/12/13/2286273.html

一、离散序列样本

　　X = [1 1 1 1 1 1   2 2 2 2 2 2    3 3 3 3 3];

　　Y= [1 2 1 1 1 1   1 2 2 2 2 3    1 1 3 3 3];

二、计算离散序列X与Y的互信息（Mutual information）

　　MI可以按照下面的公式(1)计算：

                                                       

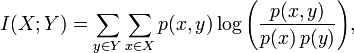
X和Y的联合分布概率p（x,y）和边缘分布律p(x)、p（y）如下：

                                                 

其中，分子p(x,y)为x和y的联合分布概率：

                                                           p(1,1)=5/17, p(1,2)=1/17, p(1,3)=0;

                                                           p(2,1)=1/17, p(2,2)=4/17, p(2,3)=1/17;

                                                           p(3,1)=2/17, p(3,2)=0, p(3,3)=3/17;                  

分母p(x)为x的概率函数，p(y)为y的概率函数，

                                                对p(x)：

                                                           p(1)=6/17,p(2)=6/17,p(3)=5/17  

                                                对p(y)：

                                                           p(1)=8/17,p(2)=5/17,P(3)=4/17 

把上述概率代入公式（1），就可以算出MI。

三、计算标准化互信息NMI（Normalized Mutual information）

　　标准化互信息，即用熵做分母将MI值调整到0与1之间。一个比较多见的实现是下面所示：

                                                             

H(X)和H(Y)分别为X和Y的熵，H(X)计算公式如下，公式中log的底b=2。

                                                      

例如，H(X) =  -p(1)*log2(p(1)) - -p(2)*log2(p(2)) -p(3)*log2(p(3))。

 

四、计算标准互信息的MATLAB程序

function MIhat = nmi( A, B ) %NMI Normalized mutual information
% http://en.wikipedia.org/wiki/Mutual_information
% http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html
% Author: http://www.cnblogs.com/ziqiao/   [2011/12/13] if length( A ) ~= length( B)
    error('length( A ) must == length( B)');
end
total = length(A);
A_ids = unique(A);
B_ids = unique(B);

% Mutual information
MI = 0;
for idA = A_ids
    for idB = B_ids
         idAOccur = find( A == idA );
         idBOccur = find( B == idB );
         idABOccur = intersect(idAOccur,idBOccur); 
         
         px = length(idAOccur)/total;
         py = length(idBOccur)/total;
         pxy = length(idABOccur)/total;
         
         MI = MI + pxy*log2(pxy/(px*py)+eps); % eps : the smallest positive number

    end
end

% Normalized Mutual information
Hx = 0; % Entropies
for idA = A_ids
    idAOccurCount = length( find( A == idA ) );
    Hx = Hx - (idAOccurCount/total) * log2(idAOccurCount/total + eps);
end
Hy = 0; % Entropies
for idB = B_ids
    idBOccurCount = length( find( B == idB ) );
    Hy = Hy - (idBOccurCount/total) * log2(idBOccurCount/total + eps);
end

MIhat = 2 * MI / (Hx+Hy);
end

% Example :  
% (http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html)
% A = [1 1 1 1 1 1   2 2 2 2 2 2    3 3 3 3 3];
% B = [1 2 1 1 1 1   1 2 2 2 2 3    1 1 3 3 3];
% nmi(A,B)% ans = 0.3646

　　为了节省运行时间，将for循环用矩阵运算代替，1百万的数据量运行 1.795723second，上面的方法运行3.491053 second；  但是这种方法太占内存空间， 五百万时，利用matlab2011版本的内存设置就显示Out of memory了。

版本一：

function MIhat = nmi( A, B )
%NMI Normalized mutual information
% http://en.wikipedia.org/wiki/Mutual_information
% http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html
% Author: http://www.cnblogs.com/ziqiao/   [2011/12/15] if length( A ) ~= length( B)
    error('length( A ) must == length( B)');
end
total = length(A);
A_ids = unique(A);
A_class = length(A_ids);
B_ids = unique(B);
B_class = length(B_ids);
% Mutual information
idAOccur = double (repmat( A, A_class, 1) == repmat( A_ids', 1, total ));
idBOccur = double (repmat( B, B_class, 1) == repmat( B_ids', 1, total ));
idABOccur = idAOccur * idBOccur';
Px = sum(idAOccur') / total;
Py = sum(idBOccur') / total;
Pxy = idABOccur / total;
MImatrix = Pxy .* log2(Pxy ./(Px' * Py)+eps);
MI = sum(MImatrix(:))
% Entropies
Hx = -sum(Px .* log2(Px + eps),2);
Hy = -sum(Py .* log2(Py + eps),2);
%Normalized Mutual information
MIhat = 2 * MI / (Hx+Hy);
% MIhat = MI / sqrt(Hx*Hy); another version of NMIend

% Example :  
% (http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html)
% A = [1 1 1 1 1 1   2 2 2 2 2 2    3 3 3 3 3];
% B = [1 2 1 1 1 1   1 2 2 2 2 3    1 1 3 3 3];
% nmi(A,B) % ans =  0.3646

版本二：

A = [1 1 1 1 1 1   2 2 2 2 2 2    3 3 3 3 3];
B = [1 2 1 1 1 1   1 2 2 2 2 3    1 1 3 3 3];
 
 if length( A ) ~= length( B)
    error('length( A ) must == length( B)');
 end
 
total = length(A);                  %17
A_ids = unique(A);                %[1,2,3]
A_class = length(A_ids);       % 3
B_ids = unique(B);                 %[1,2,3]
B_class = length(B_ids);        %3

% Mutual information
idAOccur = double (repmat( A, A_class, 1) == repmat( A_ids', 1, total ));
idBOccur = double (repmat( B, B_class, 1) == repmat( B_ids', 1, total ));
idABOccur = idAOccur * idBOccur';
Px = sum(idAOccur') / total;
Py = sum(idBOccur') / total;
Pxy = idABOccur / total;
miMatrix = Pxy .* log2(Pxy ./(Px' * Py)+eps);  %加上一个很小的数，log2的真数部分不能<=0.
mi = sum(miMatrix(:));

% Entropies(熵)
Hx = -sum(Px .* log2(Px + eps),2);
Hy = -sum(Py .* log2(Py + eps),2);

%Normalized Mutual information
nmi= 2 * mi / (Hx+Hy)   % nmi = mi / sqrt(Hx*Hy); another version of nmi