二项堆
可合并堆,支持五种操作:
MAKE-HEAP()INSERT(H, x)MINIMUM(H): 返回一个指向堆 H 中包含最小关键字的节点的指针EXTRACT-MIN(H):将堆 H 中包含最小关键字的节点删除,并返回一个指向该节点的指针。UNION(H1, H2): 创建并返回一个包含堆 H1 和 H2 中所有节点的新堆。同时删除原 H1 和 H2
二项堆和斐波那契堆支持的额外两种操作:
DERCREASE-KEY(H, x, k): 将新关键字值 k 赋给堆 H 中的节点 x,k 值小于 x.keyDELETE(H, x)
当不需要合并操作时,二叉堆就可以满足要求,但是当执行 UNION 时,二叉堆的时间复杂度达到 O(n)

上图中斐波那契堆的时间界是平摊时间界
二项树与二项堆
一个二项堆由一组二项树所构成,
二项树
递归定义:二项树 \(B_{k}\) 由 2 棵二项树 \(B_{k-1}\) 连接而成:其中一棵树的根是另一颗树的根的最左孩子。
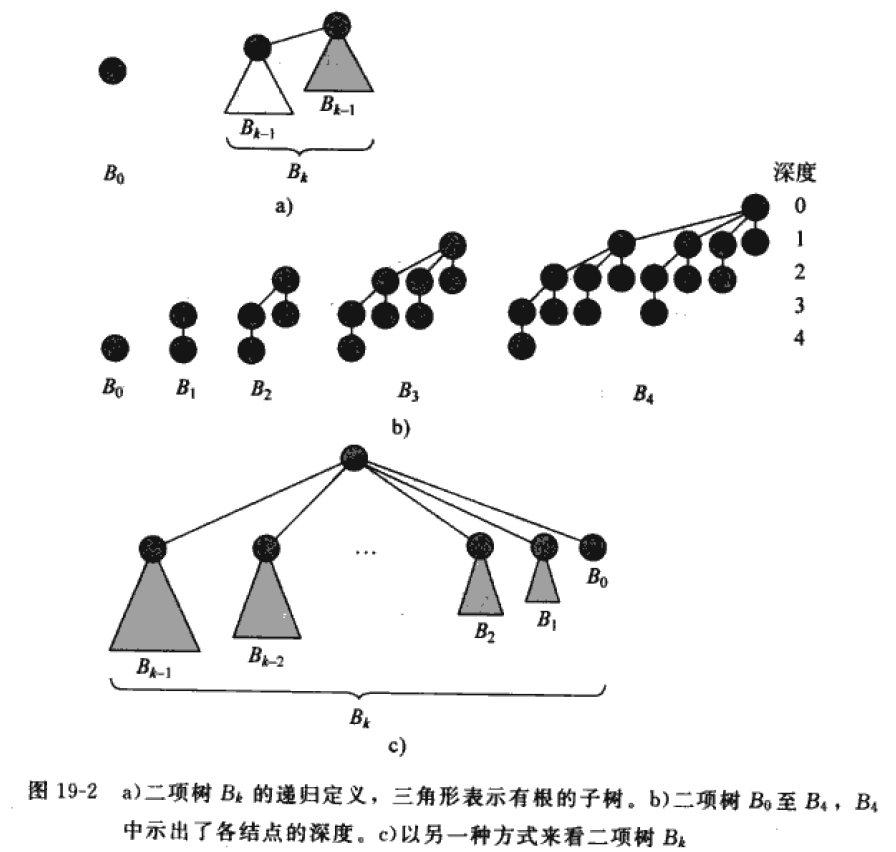
二项树\(B_{k}\)的性质
- 共有 \(2^{k}\) 个节点
- 树的高度为 k
- 在深度 i 处恰有\(\left( \begin{matrix} k \\ i \end{matrix}\right)\)个节点,其中i从0到k
- 根的度数为 k,它大于任何其他节点的度数;并且如果根的子女节点从左到右编号为 k-1, k-2, ..., 0, 子女 i 是子树 \(B_{i}\) 的根。
推论: 在一棵包含 n 个节点的二项树中,任意结点的最大度数为\(\log_{2} n\)
二项堆
二项堆 H 由一组满足下面的二项堆性质的二项树组成。
- H 中的每个二项树遵循最小堆性质:节点的关键字大于或等于其父节点的关键字
- 对任意非负整数k,在 H 中至多有一颗二项树的根具有度数 k。
由性质 1 知道:一个最小堆有序二项树中,其根包含了树中最小的关键字;
关于性质二:
对于包含 n 个节点的二项堆,必须满足性质二,而如何才能满足性质二呢?
想到 n 的二进制表示。将 n 表示为二进制后,第 i 位的 1 或者 0 刚好表示要构成 n 是否需要该 \(2^i\)。而二项树 \(B_{k}\)共有\(2^{k}\)个结点,他的根的度刚好为k!!你说巧不巧??!!
还不懂?简而言之,就是如何判断一个包含 n 个元素的二项堆由哪几个二项树构成呢?将 n 写成二进制形式,哪一位为 1,那一位对应的二项树就应该存在。
比如包含13个节点的二项堆,13的二进制表示为1101,那么该二项堆由二项树\(B_{3}\)\(B_{2}\)和\(B_{0}\)构成。
这样又推出:含有 n 个节点的二项堆最多有\(\lfloor lgn \rfloor + 1\)棵二项树。
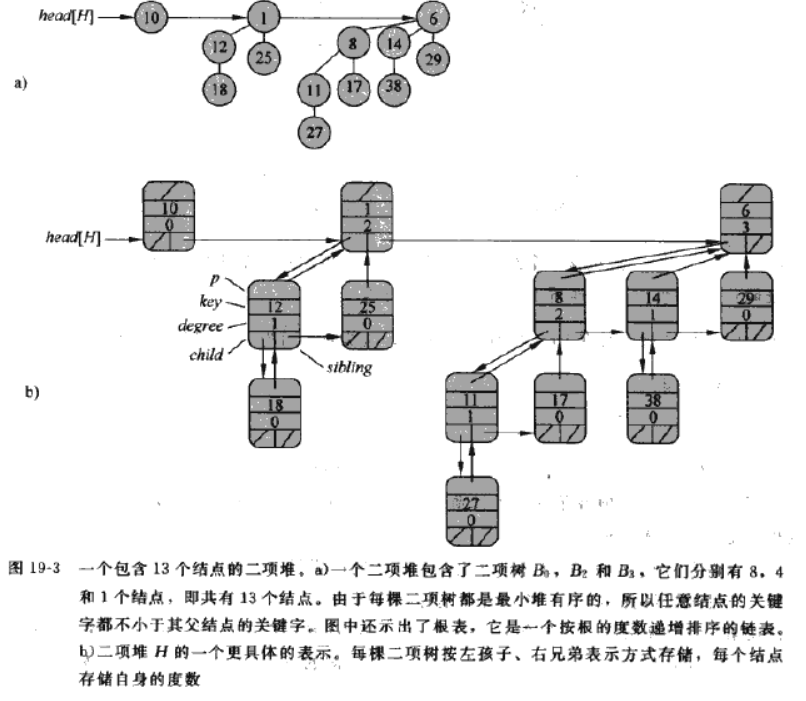
二项堆中所有二项树的根结点被组织成一个链表,称之为根表。在遍历根表时,各根的度时严格单调递增的。
对二项堆的操作
创建一个新二项堆
MAKE-BINARY-HEAP
寻找最小关键字
BINOMIAL-HEAP-MUINIMUM
二项堆是最小堆有序的,所以最小关键字一定在二项树根节点中。遍历根表将指向最小关键字根节点的指针赋给y。
y <- NUL
x <- head[H]
min <- ∞
while x != NIL
do if key[x] < min
then min <- key[x]
y <- x
x <- sibling[x]
return y
由前面分析知道,根表最多有\(\lfloor lgn \rfloor + 1\)课二项树,所以寻找最小关键字操作的运行时间为\(O(lg n)\)
合并两个二项堆
合并两个二项堆的运行时间为O(lgn)
BINOMIAL-HEAP-UNION 反复连接根节点的度数相同的二项树。
需要几个单独子过程:
BINOMIAL-LINK将以节点 y 为根的\(B_{k-1}\)树与以节点 z 为根的\(B_{k-1}\)连接起来,并且使得 z 成为 y 的父节点,成为一棵\(B_{k}\)树的根。
BINOMIAL-LINK(y, z)
p[y] <- z
sibling[y] <- child[z]
child[z] <- y
degree[z] <- degree[z] + 1
BINOMIAL-HEAP-MERGE(h1, h2)将 h1 和 h2 的根表合并成一个按度数单调递增次序排列的链表。
BINOMIAL-HEAP-MERGE(h1, h2)
dummy <- new root;
cur <- dummy;
while(h1 != NIL && h2 != NIL)
if(degree[h1] <= degree[h2])
sibling[cur] <- h1
h1 <- sibling[h1]
else
sibling[cur] <- h2
h2 <-sibling[h2]
cur <- sibling[cur]
if(h1 != NIL)
sibling[cur] <- h1
else
sibling[cur] <- h2
return sibling[dummy]
下面是合并二项堆的伪代码:
BINOMIAL-HEAP-UNION(h1, h2)
h <- MAKE-BINOMIAL-HEAP()
head[h] <- BINOMIAL-HEAP-MERGE(h1, h2)
if head[h] = NIL
return H
prev-x <- NIL
x <- head[h]
next-x <- sibling[x]
while next-x != NIL
do if(degree[x] != degree[next-x]) or
(sibling[next-x] != NIL and degree[sibling[next-x]] = degree[x])
then prev-x <- x *Cases 1 and 2
x <- next-x *Cases 1 and 2
else if key[x] <= key[next-x]
then sibling[x] <- sibling[next-x] *Cases 3
BINOMIAL-LINK(next-x, x) *Cases 3
else if prev-x = NIL *Cases 4
then head[h] <- next-x *Cases 4
else sibling[prev-x] <- next-x *Cases 4
BINOMIAL-LINK(x, next-x) *Cases 4
x <- next-x
next-x <- sibling[x]
return h
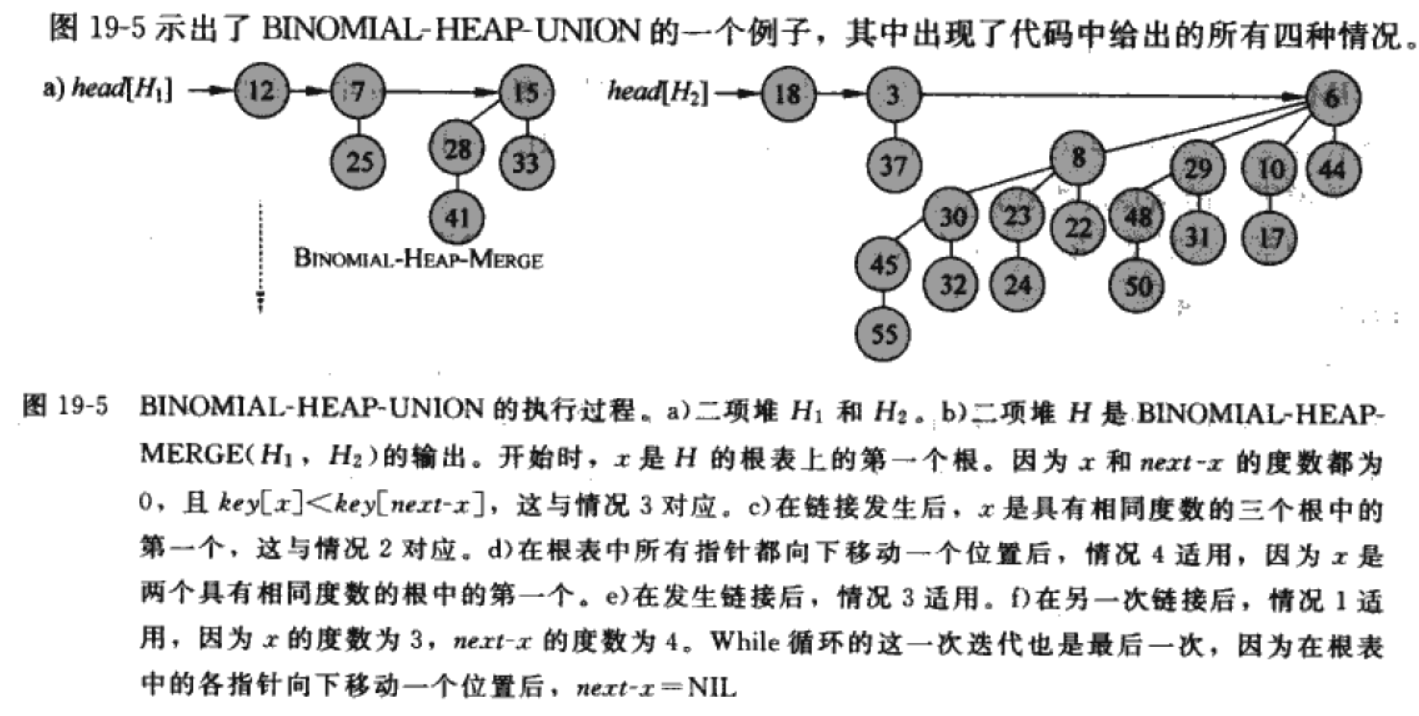
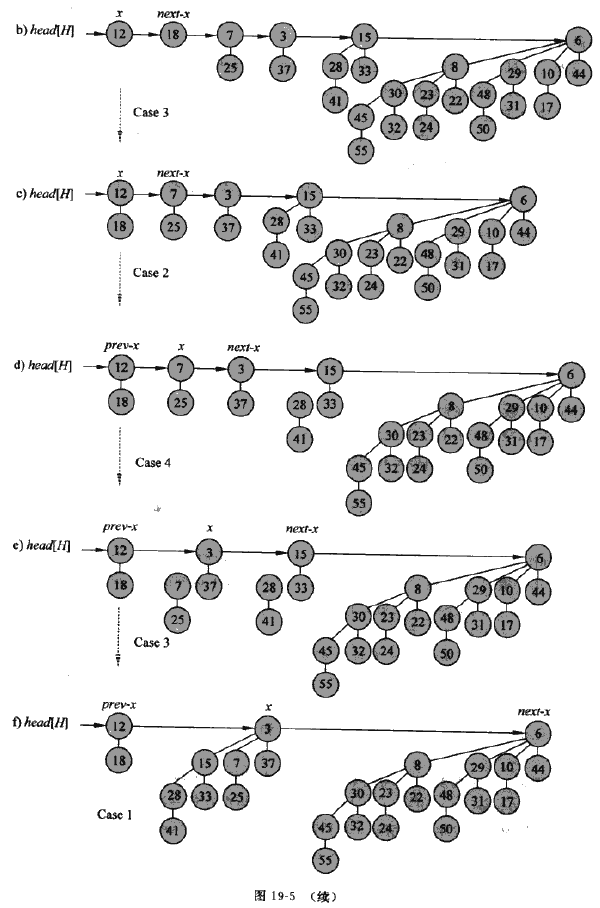
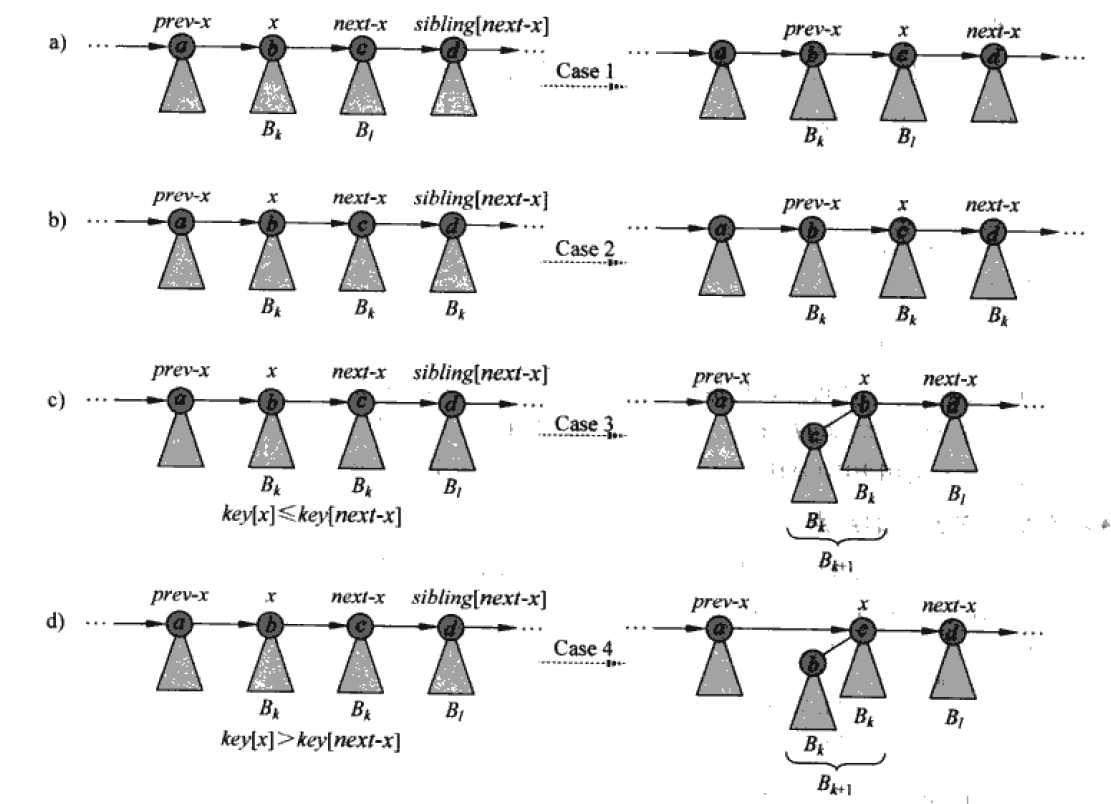
合并过程其实可以总结为:
- 首先通过 BINOMIAL-HEAP-MERGE 将 h1 h2 的根表合并为 degree 单调递增的根表, prev-x、x、next-x 表示对链表进行操作用到的指针,记为操作指针
- 如果 degree[x] != degree[next-x] ,或者 degree[x] = degree[sibling[x]] (三个连续根的degree相等,只需要合并后面两个根),那么操作指针集体后移一位
- 如果 degree[x] = degree[next-x] 那么按照正确的key关系将 x 和 next-x 合并成新二项树
插入一个结点
构造一个只带插入结点 x 的二项堆,然后把该二项堆和原二项堆合并。
BINOMIAL-HEAP-INSERT(H, x)
H' <- MAKE-BINOMIAL-HEAP()
p[x] <- NIL
child[x] <- NIL
sibling[x] <- NIL
degree[x] <- 0
head[H'] <- x
H <- BINOMIAL-HEAP-UNION(H, H')
抽取具有最小关键字的节点
首先从根表中找到具有最小关键字的根,然后将这个根从其对应的二项树 \(B_{k}\) 中删除,该根的度为 k ,那么将这 k 棵子树组成一个新的二项树,再和原先根表中二项树组成的二项堆合并。
BINOMIAL-HEAP-EXTRACT-MIN(H)
find the root x with the minimum key in the root list of H, and remove x from the root list of H
H' <- MAKE-BINOMIAL-HEAP()
reverse the order of the linked list of x's child, and set head[H'] to point to the head of the resulting list
H <- BINOMIAL-HEAP-UNION(H, H')
return x

减小关键字的值
将二项堆 H 中的某一个节点 x 的关键字减小为一个新值 k
BINOMIAL-HEAP-DECREASE-KEY(H, x, k)
if k > key(x)
then error "new key is greater than current key"
key[x] <- k
y <- x
z <- p[y]
while z != NIL and key[x] < key[z]
do exchange key[x] <-> key[z]
y <- z
z <- p[y]
说人话就是将 x 的 key 设置为 k, 如果 k 比 key[p[x]] 小,那么执行类似冒泡排序的过程将 x 和 p[x] 的key交换,直到满足条件或者 x 变为根节点
删除一个节点
从二项堆 H 中删除节点 x
就是将结点 x 的 key 值设置为无穷小,然后通过 BINOMIAL-HEAP-DECRESE-KEY 以一个类似冒泡的过程将该节点上浮到根结点,再将二项堆根表中的这个结点删除。
BINOMIAL-HEAP-DELETE(H, x)
BINOMIAL-HEAP-DECRESE-KEY(H, x, -∞)
BINOMIAL-HEAP-EXTRACT-MIN(H)



