[外文翻译] 跳表(Skip List)
Skip Lists: A Probabilistic Alternative to Balanced Trees
[TOC]
可以使用跳表来代替平衡树。跳表使用随机化来实现平衡(probabilistic balancing),而不是使用严格操作限制来实现平衡(strictly enforced balancing)。因此在跳表中进行插入和删除会比在平衡树中更快更简单。
平衡树可以用来实现例如字典以及有序表等抽象数据结构。当元素以随机的顺序插入时,平衡树的效果很好。然而在一些序列化操作,比如依顺序插入元素时,可能会产生性能非常差的数据结构。如果有可能将元素列表重新随机排列,那么平衡树将会对序列化输入数据具有很好的性能。而在大多数情况下,查询操作需要在线解答(立刻得到答案)。因此随机排序查询顺序是不可行的。平衡树算法在执行操作时重新排列树,以保持一定的平衡条件,保证良好的性能。
跳表(Skip lists)是对平衡树的一个probabilistic alternative。跳表通过查询一个随机数产生器来实现平衡。尽管跳表在最差情况下的性能很差,但是没有哪个输入序列能够始终产生最差的性能(很像随机选择主元素时的快速排序)。对于一个跳表来说,它变得及其不平衡是不太可能的(比如,对于一个具有250个元素的字典,查询操作会花费预期时间3倍的概率不超过一百万分之一)。跳表的平衡性很像通过随机插入构造的搜索树的平衡性,然而跳表的平衡性并不需要严格的随机插入。
Balancing a data structure probabilistically is easier than explicitly maintaining the balance. 对于许多应用而言,跳表是一个更加自然的选择,并且相比平衡树实现更简单。
Skip Lists
对于一个linked list来说,如果要查找某个元素,我们可能需要遍历整个链表。如果list是有序的,并且每两个结点都有一个指针指向它之后两位的结点(Figure 1b),那么我们可以通过查找不超过$\lceil \frac{2} \rceil + 1$个结点来完成查找。如果每四个结点都有一个指针指向其之后四位的结点,那么只需要检查最多$\lceil \frac{4} \rceil + 2$个结点(Figure 1c)。如果所有的第$(2^)$个结点都有一个指针指向其$2^\(之后的结点(Figure 1d),那么最大需要被检查的结点个数为\)\lceil log_2 \rceil$,代价仅仅是将需要的指针数量加倍。这种数据结构的查询效率很高,但是对它的插入和删除几乎是不可实现的。
一个具有 k 个forward pointers的结点称为一个level k结点。如果每$2^$个结点都有一个指向其之后第$2^$结点的指针,那么所有结点的level就是一个很简单的分布:50%的结点是level 1,25%的结点是level 2,12.5%的结点是level 3 and so on。如果我们随机选择结点的level,并且还要保持相同的性质,结果会如何呢(Figure 1e)?这会导致一个结点的第i个forward pointer指向下一个level为 i 或者更高的结点,而不是指向之后第$2^$个结点。
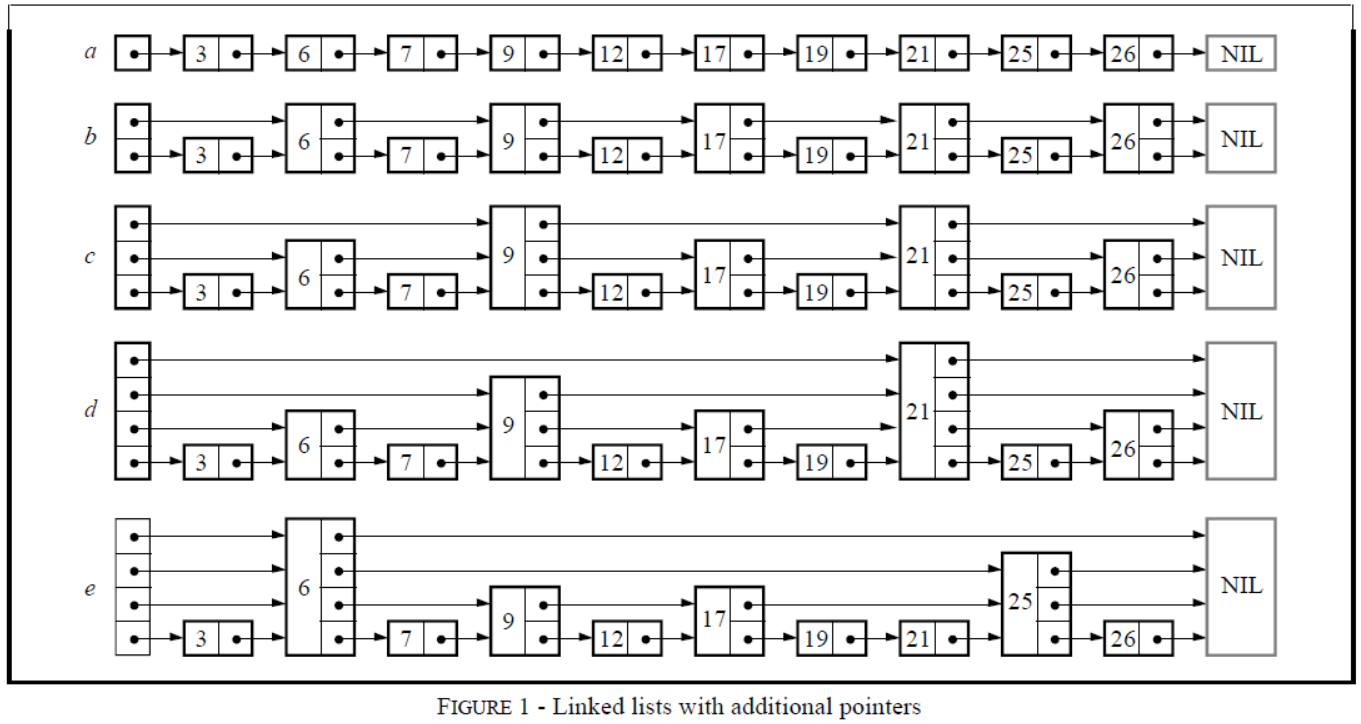
这样,插入和删除操作只需要进行本地修改;结点的level会在结点被插入时随机地选择,并且永远不会被改变。有时候对level的选择会导致很差的执行时间,但是后面我们会发现,这种情况其实很罕见。因为这些数据结构是具有额外指针的链表,这些额外指针会跳过中间的内部结点,所以称这种数据结构为跳表。
Skip List Algorithm
介绍基本操作:
Search操作返回目标关键字所关联的value,如果没有该关键字则返回failure
Insert操作对目标关键字更新value,如果目标关键字不存在,则将关键字插入
Delete操作删除目标关键字。
像类似Find the minimum key以及find the next key的额外操作较容易实现。
每个元素以结点的形式存在,每个结点的level都是在插入时随机选择的。一个level i结点中有i个前向指针,索引从 1 到 i。结点的level被控制在一个适当的常数MaxLevel范围内。Skip List的level是当前list中的最大level。The header of a list has forward pointers at levels one through MaxLevel.在高于列表当前最大level的级别上,头的向前指针指向NIL。
Initialization
空结点 NIL 中的关键字比所有有效结点中的关键字都大。新产生的list的level为1,并且list's header的所有forward pointers指向NIL。
Search Algorithm
通过遍历所有含有不超过目标关键字的结点的前向指针,我们来对目标进行搜索。

当在当前level中没有满足条件的forward pointers之后,去下一层level继续搜索。当在level 1中没有满足条件的结点之后,那下一个结点就是我们所要搜索的包含目标关键字的结点。
Insertion and Deletion Algorithm
为了添加或者删除一个结点,我们只需要进行搜索以及拼接,正如Figure 3所示。
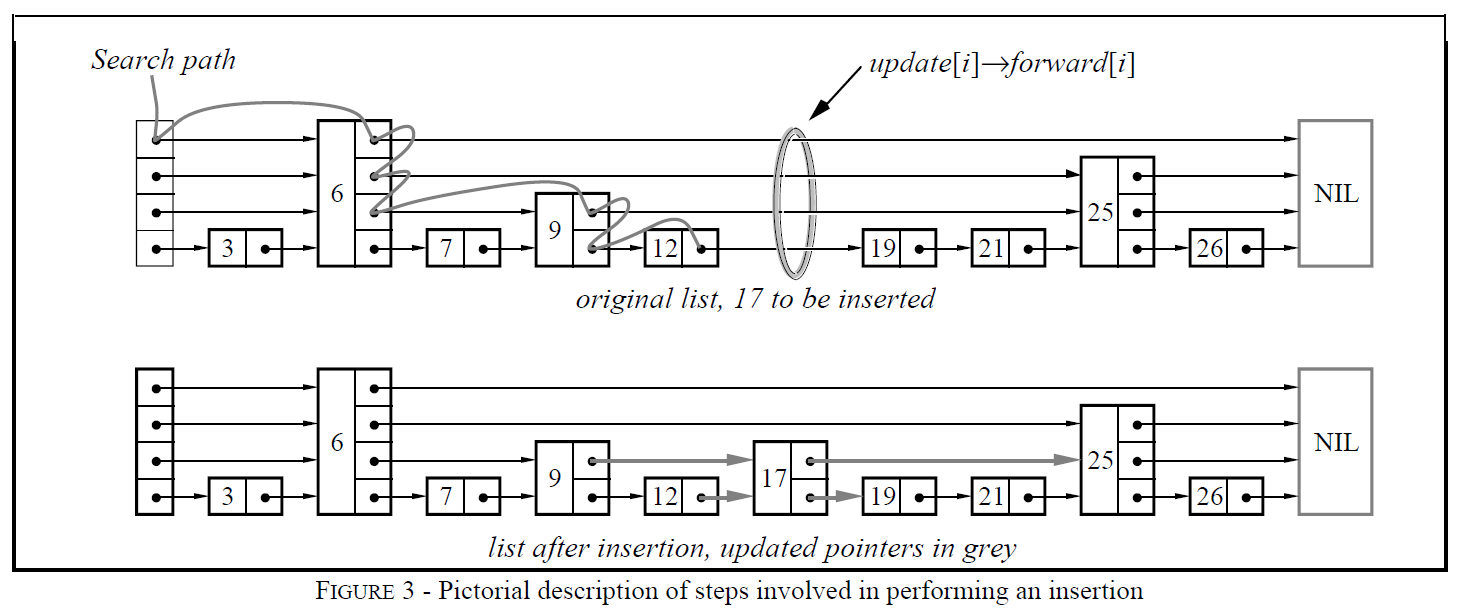
搜索结束时,向量update中的元素update[i]保存一个指针,该指针指向search结束位置所有左侧结点中,最靠右边的level i结点。
如果插入操作产生了一个比之前list中最大level还大的结点,那么我们需要更新the maximum level of the list并且初始化update向量的适当的部分。在每次删除之后,我们会检查是否删除了list中的最大level结点。如果删除了也需要更新maximum level of the list。

Choosing a Random Level
起初我们论证了,具有level i前向指针的结点中的一半也会具有level i+1指针。我们可以说,p比例的level i结点中会包含level i+1前向指针。Level是由Figure 5中的类似算法随机产生的。

At what level do we start a search? Defining L(n)
在一个$p=\frac{1}{2}$,具有16个元素的跳表中,可能恰巧有9个level 1结点,3个level 2结点,三个level 3结点和一个level 4结点。如果如果我们使用标准搜索算法, 从level 4开始搜索,会做很多无用功。
我们的分析显示,理想情况下,我们应该在具有$\frac{1}$个结点的Level L处开始搜寻。此时$L=log_{\frac{1}}n$(原论文中是这个,但我觉得应该是$L=lon_{\frac{1}}n-1$?),由于我们会频繁使用这个公式,所以简记为L(n)。
Skip List中有时会出现在某个不寻常的level上只有一个元素的情况,有如下三种解决方法:
Don't worry, be happy. 依然在list中的最高level上开始搜索。正如将在分析中看到的那样,一个n结点的list中的最高
level大于L(n)的概率是非常小的。从最高level开始搜索仅仅会对最终的预期搜索时间添加一个常数时间项。这也是我们所采用的方法。Use less than you are given. 尽管某个元素可能会具有14个指针,我们并不需要使用所有的14个指针。我们可以只选择使用L(n)。有很多方法实现这种策略,但是实际带来的提升并不是很明显,因此并不推荐这种方法。
Fix the dice. 如果产生一个比当前maximum level更大的结点,那么我们将新节点的
level设置为current maximum level + 1。直觉上来看,这种方法似乎很好,但是实际上它会完全摧毁我们所有分析的基础:因为结点的level不再是随机值。
Determining MaxLevel
如前所述,设置最大level为L(N),可以保证我们快速地执行搜索。此处N表示跳表中所有元素的一个上界。如果p=1/2,那么对于一个包含$2^{16}$个元素的跳表来说,选择Maximum Level为16是一个适当的选择。
Analysis of Skip List Algorithm
执行Search, Delete and Insert操作需要的时间由搜素目标元素的时间决定。对于Insert 和 Delete操作来说,有一个额外开销,该开销与被操作结点的level成比例。 寻找指定元素需要的时间与搜索路径的长度成比例,搜索路径则是由当我们遍历list时遇到的结点的level所决定。
Probabilistic Philosophy
跳表的结构仅仅由其中元素的数量以及随机数产生器的结果决定。
Analysis of expected search cost
我们从下往上从右往左分析搜索路径。
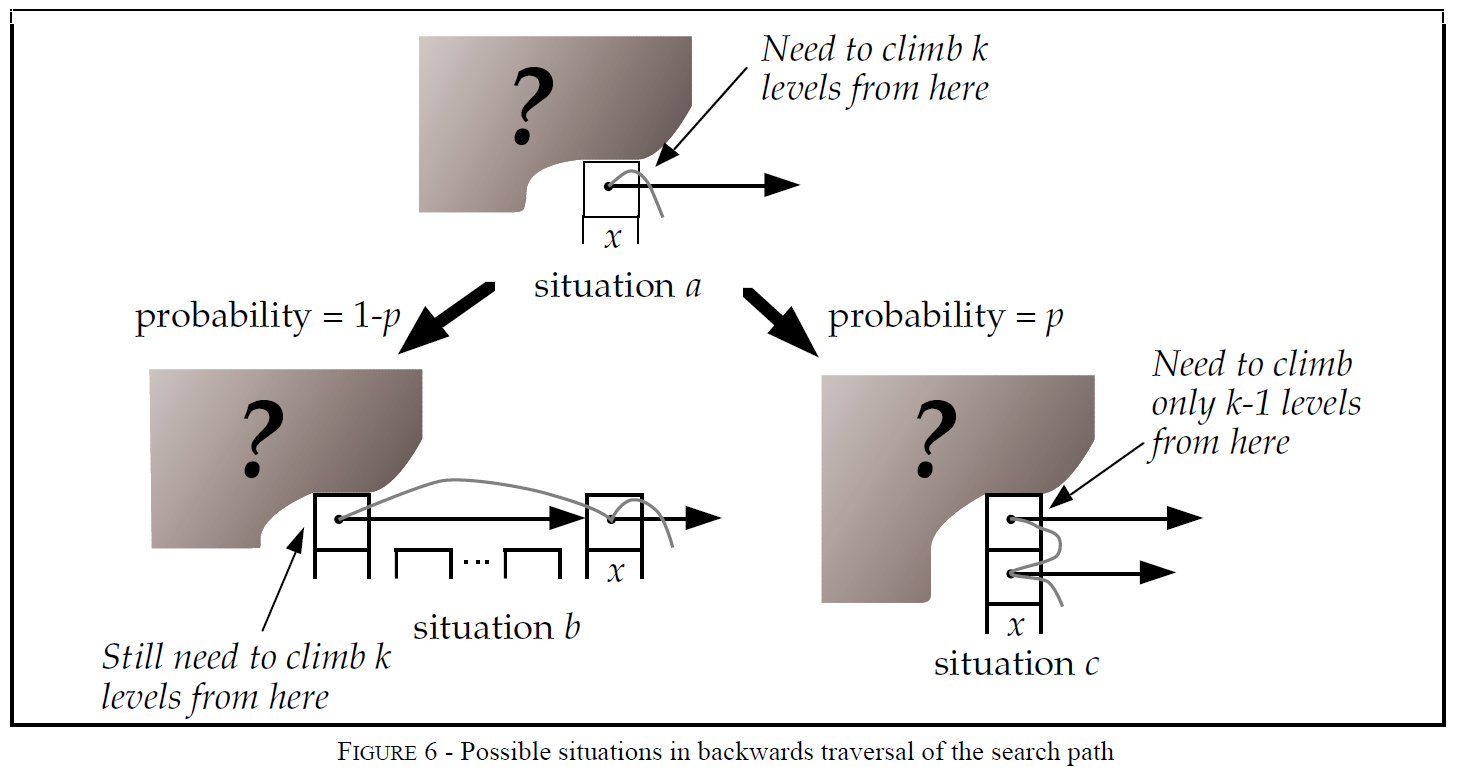
在climb的每个结点,我们都与Figure 6中 a 的情况相似————我们是结点 x 的第 i 个前向指针,并且我们不知道 x 左侧结点的 level,也不知道 x 的 level。假设 x 不是头结点。如果level of x是 i,那么就是情况 b,如果 x 的level比 i 大,那么就是情况 c。我们处于情况 c 的概率为 p(level i 结点中,有 p 比例的结点同时也是 level i+1 结点)。当我们处于情况 c 时,我们总是会 climb up a level。假设 C(k) 表示在一个无限的list中,向上爬 k 层需要的代价。那么有:

当我们向上爬爬到Head时,就不再进行左移。那么在一个 n 个元素的跳表中,从level 1爬到level L(n)的预期路径长度的上界为:(L(n)-1)/p。对于剩余的左移部分,level L(n)上结点数量的期望为 1/p,所以剩余的左移的期望代价为1/p。
跳表的最大高度大于list的可能性为$1-(1-p^)$,接近$np$。
Putting our results together, we find:
Total expected const to climb out of a list of n elements ⇐ L(n)/p + 1/(1-p), which is O(log n)
Number of comparisons
one plus the length of the search path.
Probabilistic Analtsis
Choosing p
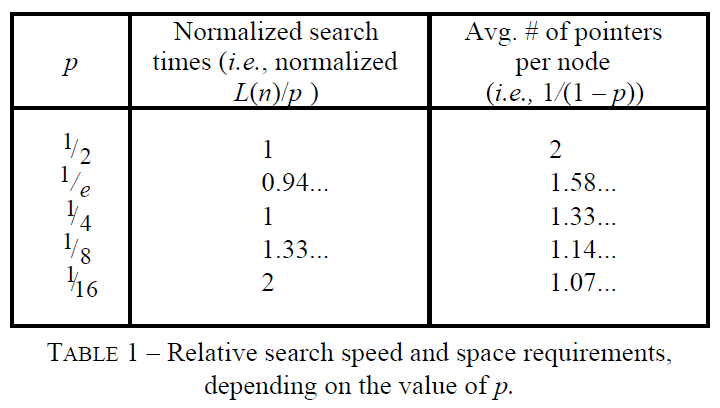
减少p也增加了运行时间的可变性(方差)。建议 p 取 1/4,如果运行时间的可变性是首要关注点(要求运行时间方差较小),那么可以选 p 为 1/2。



