《<最小联通块>命题报告》学习笔记
《<最小联通块>命题报告》学习笔记
论文搬运工++
loj提交地址
暴力算法
算法 1.1
直接 \(O(n^2)\) 枚举 \(\{u,v\}\)，然后再 \(O(n)\) 对于每个 \(w\) 判断 \(w\) 是否在 \(u\to v\) 上，复杂度 \(O(n^3)\)
算法 1.2
假设以 \(1\) 为根，那么对于每一个点 \(u\)，我们可以通过 \(query(\{1,u\},w)\) 询问出它的祖先集合，那么某个点的父亲就是祖先集合包含于它的且集合最大的那个点，复杂度 \(O(n^2)\)。
算法 1.3
首先我们考虑怎么样找到一个点 \(u\) 任意一个的子孙节点：假设目前可能的答案集合为 \(S\)，每次得到一个大小为 \(S\) 一半的集合 \(T\)，\(query(\{1\cup T\},u)\)，如果 \(T\) 中存在答案，那么令 \(S=T\)，否则 \(S=S-T\)。其实就是一个二分，单次寻找的复杂度为 \(O(\log n)\)，如果还想找另外一个就直接把当前找到的点去掉再找就好了。
我们考虑把整棵树当做一颗内向树，然后假定我们已经弄出这棵树的任意一个合法的拓扑序。
那么我们可以按拓扑序从小往大扫描每个点，找到当前点的每个子孙节点并将这些点从点集中去掉，容易知道这样的话除 \(1\) 外每个点只会被作为儿子节点找到一次，复杂度 \(O(n\log n)\)。
直接暴力把拓扑序找出来就是一层层剥叶子，每次去掉一个点 \(u\) 看这个点还在不在 \(V-u\) 中，复杂度 \(O(n^2)\)。
注意此算法中的利用拓扑序的思想，下面算法均在 “找到拓扑序” 中展开。
基于剥叶子的算法
算法 2.1
注意到上面 1.3 每次找叶子的复杂度是 \(O(n)\) 的，我们想办法优化找叶子的过程。
我们利用我们 1.3 中所讲的找子孙节点的方法，每次找到任意一个子孙并往下跳，跳不动了则找到了一个叶子。
考虑这么做的复杂度：一个节点 \(u\) 子孙中大小超过 \(\lceil \frac {size_u}{2}\rceil\) 的节点最多占到一半，所以我们期望跳两次就可以使当前所在点的子树大小减半，跳的期望次数是 \(O(\log n)\) 级别的，每次跳复杂度 \(O(\log n)\)，所以总复杂度就是 \(O(n\log ^2n)\)。
算法 2.2
还有一种剥叶子的方法就是考虑优化剥叶子的轮数。
考虑到如果我们当前这棵树上没有 \(2\) 度点，那么总轮数就是 \(O(\log n)\) 级别的。
我们建出当前这棵树的虚树：即把一个度数为 \(2\) 的点删去，然后将该点相邻的两点连边，递归执行此过程，留下的树就是虚树。
考虑如果我们每次可以剥掉虚树上每个叶子和叶子所连的那条链上的所有点，我们可以保证复杂度。
考虑找出所有这样的点，拿出叶子集合 \(L\)，然后每次 \(2\log n\) 找当前点集里只存在一个叶子的点，这样可以找到很多条链，再将每条链从上到下排好序即可。
最后的复杂度是 \(O(n\log ^2n)\)。
基于分治的算法
算法 3.1
我们现在考虑从分治的角度入手。
假设当前在点 \(x\)，我们随机找到其子树内的一个点 \(y\)，我们确定 \(y\) 子树内的点集后，可以将 \(x\) 的子树划分为 \(2\) 个部分，继续递归执行操作。
如果像平常点分治那么做复杂度显然假假，我们考虑将 \(y\) 删去后所有联通块染成了若干种不同的颜色。
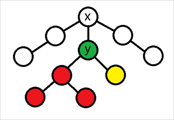
我们的目的就是判断每个点是否为白色。
考虑将所有点按编号拍成一行：
那么我们可以确定每个极长颜色段的分割点，确定完之后和 \(1\) 查询就可以知道每个段是否是白色的了，然后每次确定一个极长的连续段利用二分是 \(O(\log n)\) 的。
整个算法的复杂度的话考虑出现次数最多的颜色，可以发现颜色总段数是 \(O(n\log n)\) 级别的，具体的这里我不想写了。。然后算法总复杂度就是 \(O(n\log ^2n)\)。
算法 3.2
事实上我们并不需要知道每个点子树外的点是什么，只需要得到一种合法的拓扑序就好了。
那么我们可以任意选择当前节点 \(u\) 子树中的一个点 \(v\)，在得到 \(v\) 中的点后将 \(v\) 中的点按原先排好的拓扑序加入当前拓扑序的末尾，对 \(v\) 同样地处理就好了，复杂度 \(O(n\log n)\)。
直接考虑拓扑序
算法 4.1
我们实际上不需要在树上做这件事，只需要加入节点时时刻保证当前维护的拓扑序合法即可。
那么我们可以每次加入一个点，它需要保证所有祖先出现在它后面，所有子孙出现在它前面，这个过程可以二分，复杂度\(O(n\log n)\)。为什么复杂度低的算法看起来还简单些啊
代码实现去 loj 找吧，这里就不放了。
