Codeforces Round #652 (Div. 2)
A. FashionabLee
签到。
Code
/*
* Author: heyuhhh
* Created Time: 2020/6/23 22:06:06
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#include <functional>
#include <numeric>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << std::endl; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
template <template<typename...> class T, typename t, typename... A>
void err(const T <t> &arg, const A&... args) {
for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
#define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
void run() {
int n; cin >> n;
if (n < 4) {
cout << "NO" << '\n';
} else {
n -= 4;
if (n % 4 == 0) cout << "YES" << '\n';
else cout << "NO" << '\n';
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
int T; cin >> T; while(T--)
run();
return 0;
}
B. AccurateLee
注意到\(1....0\)这样的形式最后一定能变为一个\(0\)。那么因为要求字典序最小,所以贪心缩一下就行。
Code
/*
* Author: heyuhhh
* Created Time: 2020/6/23 22:09:22
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#include <functional>
#include <numeric>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << std::endl; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
template <template<typename...> class T, typename t, typename... A>
void err(const T <t> &arg, const A&... args) {
for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
#define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
void run() {
int n; cin >> n;
string s; cin >> s;
int fir = n, last = -1;
for (int i = 0; i < n; i++) {
if (s[i] == '1') {
fir = i;
break;
}
}
for (int i = n - 1; i >= 0; i--) {
if (s[i] == '0') {
last = i;
break;
}
}
for (int i = 0; i < fir; i++) {
cout << s[i];
}
if (fir < last) {
cout << 0;
}
for (int i = last + 1; i < n; i++) {
cout << s[i];
}
cout << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
int T; cin >> T; while(T--)
run();
return 0;
}
C. RationalLee
贪心分配即可。
首先最大的\(k\)个数一定会产生一次贡献,其次最小的那个数也一定会产生一次贡献。
现在是要使得每组中最小值之和最大。所以按照\(w_i\)从大到小排序,后面较小的值能放就放,这样能使得每组最小值尽可能大。
注意\(w_i=1\)的组最大值会产生两次贡献,那么直接将其钦定为尽可能大的贡献即可。
代码如下:
Code
/*
* Author: heyuhhh
* Created Time: 2020/6/23 22:33:03
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#include <functional>
#include <numeric>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << std::endl; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
template <template<typename...> class T, typename t, typename... A>
void err(const T <t> &arg, const A&... args) {
for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
#define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
void run() {
int n, k; cin >> n >> k;
vector <int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
vector <int> w(k);
for (int i = 0; i < k; i++) {
cin >> w[i];
}
vector <int> p(n), p2(k);
iota(all(p), 0);
iota(all(p2), 0);
sort(all(p), [&](int i, int j) {return a[i] > a[j];});
sort(all(p2), [&](int i, int j) {return w[i] > w[j];});
ll ans = 0;
for (int i = 0; i < k; i++) {
ans += a[p[i]];
}
int t = n - 1, l = 0;
for (int i = 0; i < k; i++) {
if (w[p2[i]] > 1) {
--w[p2[i]];
ans += a[p[t]];
t -= w[p2[i]];
} else {
ans += a[p[l++]];
}
}
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
int T; cin >> T; while(T--)
run();
return 0;
}
D. TediousLee
题意:
定义一个类似于树一样的东西,一开始有一个结点,之后每一时刻将发生以下变化:
- 若一个结点没有儿子,则增加一个儿子;
- 若一个结点有一个儿子,则增加两个儿子;
- 若一个结点有超过两个儿子,则不变。
类似于下图:
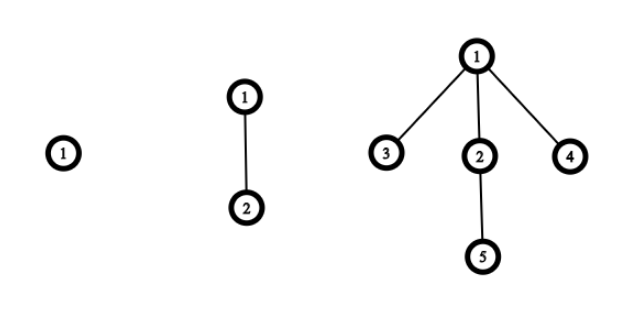
依次为\(t=1,2,3\)的情况。
现在要给尽可能多的点染色,要求一定是如下这样:
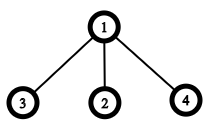
并且还没被染过色。
输出最大染色点数。
思路:
基本思想还是贪心,染色肯定自下往上染最优。
考虑图像的变化情况,对于\(n\)时刻,我们记其答案为\(f(n)\),那么其中间那个儿子的状态为\(n-1\)时刻,两边的儿子状态为\(n-2\)时刻。所以很容易得到转移式子:
- \(f(n)=f(n-1)+2\cdot f(n-2)\)
注意我们还可能将当前根节点染色,前提是其三个儿子都没染色,所以用一个\(g\)转移一下是否能染色就行。
其实也不用转移,如果\(n\%3\)当前一定能够染色。
详见代码:
Code
/*
* Author: heyuhhh
* Created Time: 2020/6/23 22:59:16
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#include <functional>
#include <numeric>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << std::endl; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
template <template<typename...> class T, typename t, typename... A>
void err(const T <t> &arg, const A&... args) {
for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
#define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 2e6 + 5, MOD = 1e9 + 7;
int f[N], g[N];
void init() {
f[3] = f[4] = 1;
g[3] = 1;
for (int i = 5; i < N; i++) {
g[i] = (g[i - 2] + g[i - 1] == 0);
f[i] = ((2ll * f[i - 2] % MOD + f[i - 1]) % MOD + g[i]) % MOD;
}
}
void run() {
int n; cin >> n;
int ans = 4ll * f[n] % MOD;
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
init();
int T; cin >> T; while(T--)
run();
return 0;
}
E. DeadLee
题意:
\(n\)种食物\(m\)个朋友,每个朋友有两种最喜欢吃的食物。
现在你每次邀请一个朋友来吃饭,这个朋友只会吃最喜欢的食物,现在每种食物有\(w_i\)份。每次每个朋友都会吃最多两份不同的最喜欢的食物。如果当前没有最喜欢的食物的话,那么就会吃了你。
现在问如何安排顺序,使得你能够活下来。
思路:
注意这个题是每个朋友最多吃两份不同的最喜欢食物,也就是如果一个人喜欢\(x_i,y_i\)并且刚好都有库存,那么就会各吃一份。
这个题很容易想到建图,对于一个朋友,我们连无向边\((x_i,y_i)\)。现在每次邀请一位朋友就会去掉一条无向边。现在已有每个点的度数\(d_i\)以及容量\(w_i\)。
注意到若某个点\(d_i\leq w_i\),那么这个菜无论怎么吃都不会吃不够,也就是对应的边都可以随意删。因为这些朋友是永远不会吃人的,所以直觉上我们将其越留在后面越棒。
因此就有了思路:从后往前贪心处理,对于某个点满足\(d_i\leq w_i\),我们枚举每条边进行删除,并且减少其它点的\(d_j\),代表现在这个食物少了一个人喜欢,也就是说让前面的人更多选择这个食物,并且尽可能吃够,而枚举的人就只吃\(i\)这种食物。
如果最后还剩下边没有删除就是不合法的情况。
很有意思的一个贪心!
Code
/*
* Author: heyuhhh
* Created Time: 2020/6/24 8:45:45
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#include <functional>
#include <numeric>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << std::endl; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
template <template<typename...> class T, typename t, typename... A>
void err(const T <t> &arg, const A&... args) {
for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
#define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
void run() {
int n, m; cin >> n >> m;
vector <int> d(n), w(n);
for (int i = 0; i < n; i++) {
cin >> w[i];
}
vector <vector <pii>> G(n);
for (int i = 0; i < m; i++) {
int u, v; cin >> u >> v;
--u, -- v;
G[u].push_back(MP(v, i));
G[v].push_back(MP(u, i));
++d[u], ++d[v];
}
queue <int> q;
for (int i = 0; i < n; i++) {
if (w[i] >= d[i]) {
q.push(i);
}
}
vector <int> ans;
vector <bool> check(m);
while (!q.empty()) {
int u = q.front(); q.pop();
for (auto it : G[u]) {
int v = it.fi, id = it.se;
if (check[id]) continue;
check[id] = true;
ans.push_back(id);
if (--d[v] == w[v]) {
q.push(v);
}
}
}
if (sz(ans) < m) {
cout << "DEAD" << '\n';
} else {
cout << "ALIVE" << '\n';
reverse(all(ans));
for (auto it : ans) {
cout << it + 1 << ' ';
}
cout << '\n';
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
run();
return 0;
}
F. BareLee
题意:
现有\(t\)回合,每一回合有两个数\(s_i,e_i\)。在每一轮游戏中,两个人轮流选择一个数\(a\)(一开始为\(s_i\)),将其变为\(2a,a+1\),如果\(a>e_i\)那么这轮游戏这个人就失败。
现在规定最后一轮赢的玩家获得整场比赛的胜利,问先手是否能赢得比赛或者先手是否能输掉比赛。注意你的对手是很聪明的,肯定不想让你轻易达到目标。
思路:
首先我们看一轮游戏中是否必胜或者必败,这涉及到分情况考虑:
我们用\(f[i][j]\)表示状态为\(i,j\)时是否必胜,\(g[i][j]\)同理表示必败。其中\(i\)为\(a\),\(j\)为\(e\)。
必胜:
- 如果\(j\)为奇数,那么\(i\)为奇数则必败,否则必胜;
- 如果\(j\)为偶数,那么:
- 若\(i>j/2\),\(i\)为偶数则必败,否则必胜;
- 若\(i>j/4\),则必胜;
- 否则问题转化为了\(f[i][j/4]\)。
必败:
- 如果\(i>j/2\),显然可以直接输掉;
- 否则问题转化为了\(f[i][j/2]\)。
那么求出每一轮的状态\(f[s_i][e_i],g[s_i][e_i]\)过后,考虑如何求出整轮游戏的状态。
我们用\(f\)表示能否先手,\(s\)表示能否后手,显然初始状态为\(f=1,g=0\)。
之后枚举每一轮,若某轮开始时\(f=s\),比如\(f=s=1\),也就是先手可以选择先手还是后手,那么之后的游戏显然他是必胜的,因为如果后面有必胜态他就必胜,否则就把问题抛给对面,这样他也是必胜。
否则就根据本轮的情况更新\(f,s\),因为现在\(f\not ={s}\),假设\(f=1\),那么显然如果有一个必败态就能继续先手,如果有一个必胜态就能后手。其余情况同理。
最后输出\(s\ f\)即可,注意顺序要反一下。
代码如下:
Code
/*
* Author: heyuhhh
* Created Time: 2020/6/24 15:08:23
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#include <functional>
#include <numeric>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << std::endl; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
template <template<typename...> class T, typename t, typename... A>
void err(const T <t> &arg, const A&... args) {
for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
#define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
int Win(ll s, ll e) {
if (e & 1) {
if (s & 1) return 0;
return 1;
}
if (s > e / 2) {
if (s & 1) return 1;
return 0;
}
if (s > e / 4) {
return 1;
}
return Win(s, e / 4);
}
int Lose(ll s, ll e) {
if (s > e / 2) {
return 1;
}
return Win(s, e / 2);
}
void run() {
int n; cin >> n;
vector <pii> r(n);
for (int i = 0; i < n; i++) {
ll s, e; cin >> s >> e;
r[i] = MP(Win(s, e), Lose(s, e));
}
int f = 1, s = 0;
for (int i = 0; i < n; i++) {
if (f == s) break;
r[i].fi ^= s;
r[i].se ^= s;
f = r[i].se;
s = r[i].fi;
}
cout << s << ' ' << f << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
run();
return 0;
}
重要的是自信,一旦有了自信,人就会赢得一切。

