【hdu5731】Solid Dominoes Tilings（打表+递推+容斥）

传送门

题意：
给定一个\(n\cdot m,n,m\leq 16\)大小的矩阵，现在要在其中放置\(1*2\)的多米诺骨牌，要求放置的方案数不能将矩阵分割成多个较小矩阵。
比如以下\((a),(b)\)合法，\((c),(d)\)不合法：

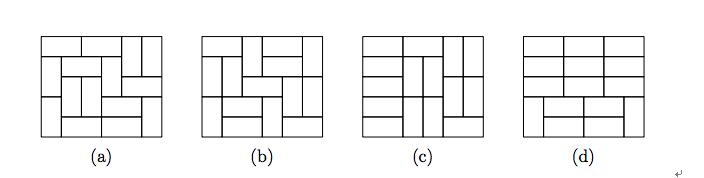
思路：
用\(dp_{i,j}\)表示大小为\(i\cdot j\)的矩阵放置多米诺骨牌的方案数。
然后枚举垂直方向进行容斥即可。
具体来说，通过\(O(2^{16})\)次方枚举矩形在垂直方向被划分的状态，在每个小矩形内，求出合法放置的数量，这里我们可以暴力递推求解：设\(f(i)\)为考虑前\(i\)行合法的方案数，那么\(\displaystyle f(i)=dp_{i,len}-\sum_{j=1}^{i-1}f(j)\cdot dp_{i-j,len}\)。我们通过总情况减去不合法的情况即可。最后再做一个容斥。
至于怎么求\(dp\)数组，直接打表吧。。直接计算复杂度下界应该是\(O(2^{2n}\cdot n)\)。
代码如下：

/*
 * Author:  heyuhhh
 * Created Time:  2020/4/10 12:05:21
 */
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#define MP make_pair
#define fi first
#define se second
#define pb push_back
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
  #define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
  void err() { std::cout << std::endl; }
  template<typename T, typename...Args>
  void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
  template <template<typename...> class T, typename t, typename... A> 
  void err(const T <t> &arg, const A&... args) {
  for (auto &v : arg) std::cout << v << ' '; err(args...); }
#else
  #define dbg(...)
#endif
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 20, MOD = 1e9 + 7;
const int dp[17][17]={0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,0,0,3,0,11,0,41,0,153,0,571,0,2131,0,7953,0,29681,0,1,5,11,36,95,281,781,2245,6336,18061,51205,145601,413351,1174500,3335651,9475901,0,0,8,0,95,0,1183,0,14824,0,185921,0,2332097,0,29253160,0,366944287,0,1,13,41,281,1183,6728,31529,167089,817991,4213133,21001799,106912793,536948224,720246619,704300462,289288426,0,0,21,0,781,0,31529,0,1292697,0,53175517,0,188978103,0,124166811,0,708175999,0,1,34,153,2245,14824,167089,1292697,12988816,108435745,31151234,940739768,741005255,164248716,498190405,200052235,282756494,0,0,55,0,6336,0,817991,0,108435745,0,479521663,0,528655152,0,764896039,0,416579196,0,1,89,571,18061,185921,4213133,53175517,31151234,479521663,584044562,472546535,732130620,186229290,274787842,732073997,320338127,0,0,144,0,51205,0,21001799,0,940739768,0,472546535,0,177126748,0,513673802,0,881924366,0,1,233,2131,145601,2332097,106912793,188978103,741005255,528655152,732130620,177126748,150536661,389322891,371114062,65334618,119004311,0,0,377,0,413351,0,536948224,0,164248716,0,186229290,0,389322891,0,351258337,0,144590622,0,1,610,7953,1174500,29253160,720246619,124166811,498190405,764896039,274787842,513673802,371114062,351258337,722065660,236847118,451896972,0,0,987,0,3335651,0,704300462,0,200052235,0,732073997,0,65334618,0,236847118,0,974417347,0,1,1597,29681,9475901,366944287,289288426,708175999,282756494,416579196,320338127,881924366,119004311,144590622,451896972,974417347,378503901};

int n, m;

void add(int &x, int y) {
    x += y;
    if(x >= MOD) x -= MOD;   
}
void dec(int &x, int y) {
    x -= y;
    if(x < 0) x += MOD;   
}

int f[N], blo[N];

void run() {
    int ans = 0;
    for(int sta = 0; sta < 1 << (m - 1); sta++) {
        int tot = 0, sz = 1;
        for(int i = 0; i < m - 1; i++) {
            if(sta >> i & 1) {
                blo[++tot] = sz;
                sz = 1;
            } else ++sz;
        }
        blo[++tot] = sz;
        memset(f, 0, sizeof(f));
        for(int i = 1; i <= n; i++) {
            f[i] = 1;
            for(int j = 1; j <= tot; j++) f[i] = 1ll * f[i] * dp[i][blo[j]] % MOD;
            for(int j = 1; j < i; j++) {
                int res = 1;
                for(int k = 1; k <= tot; k++) {
                    res = 1ll * res * dp[i - j][blo[k]] % MOD;
                }
                dec(f[i], 1ll * f[j] * res % MOD);
            }
        }
        if(tot & 1) add(ans, f[n]);
        else dec(ans, f[n]);
    }
    cout << ans << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
    while(cin >> n >> m) run();
    return 0;
}