Codeforces Round #619 (Div. 2)
A. Three Strings
签到。
Code
/*
* Author: heyuhhh
* Created Time: 2020/2/13 22:36:05
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 100 + 5;
char a[N], b[N], c[N];
void run(){
cin >> (a + 1) >> (b + 1) >> (c + 1);
int n = strlen(a + 1);
for(int i = 1; i <= n; i++) {
if(c[i] == a[i] || c[i] == b[i]) {}
else {
cout << "NO" << '\n';
return;
}
}
cout << "YES" << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
int T; cin >> T;
while(T--) run();
return 0;
}
B. Motarack's Birthday
贪心,我们把所有关键数字拿出来处理即可。
Code
/*
* Author: heyuhhh
* Created Time: 2020/2/13 22:39:33
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
int n;
int a[N];
void run(){
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
a[n + 1] = 0;
int Max = -INF, Min = INF, d = -INF;
for(int i = 1; i <= n; i++) {
if(a[i] >= 0 && (a[i - 1] == -1 || a[i + 1] == -1)) {
if(a[i] < Min) {
Min = a[i];
}
if(a[i] > Max) {
Max = a[i];
}
}
if(i > 1 && a[i - 1] >= 0 && a[i] >= 0) {
d = max(d, abs(a[i - 1] - a[i]));
}
}
if(Max == -INF) {
cout << 0 << ' ' << 0 << '\n';
} else {
d = max(d, (Max - Min + 1) / 2);
cout << d << ' ' << (Min + Max) / 2 << '\n';
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
int T; cin >> T;
while(T--) run();
return 0;
}
C. Ayoub's function
题意:
定义\(f(s):(l,r)\)的对数,满足\(01\)串\(s\)中\(s_l,s_{l+1},\cdots,s_r\)中至少有一个为\(1\)。
现在给出\(n,m\),表示\(s\)串长度为\(n\),有\(m\)个\(1\)。
现在问安排过后,最大的\(f(s)\)为多少。
思路:
考虑容斥,答案即为总方案数减去每段连续\(0\)的贡献。
容易证明只需要将\(n-m\)个\(0\)尽可能地平均分配即可。
简易证明如下:
- 首先证明分为\(m+1\)份最优,假设现在分了\(x,x<m+1\)份,某份长度为\(l\),因为可以再分,我们将其分为两份,显然最终\(0\)的总贡献会减少。
- 然后证明尽可能地平均分配。思路和上面类似,考虑两份\(0\)的个数相等或者相差不超过\(1\),然后移动一个\(0\)到另外一边,分析贡献的变化即可。
代码如下:
Code
/*
* Author: heyuhhh
* Created Time: 2020/2/13 22:52:09
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
int n, m;
void run(){
cin >> n >> m;
ll ans = 1ll * n * (n + 1) / 2;
int d = (n - m) / (m + 1);
int r = (n - m) % (m + 1);
ans -= 1ll * r * (d + 1) * (d + 2) / 2;
ans -= 1ll * (m + 1 - r) * (d + 1) * d / 2;
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
int T; cin >> T;
while(T--) run();
return 0;
}
D. Time to Run
题意:
给出一个\(n*m\)的矩阵,相邻格子之间都有双向边。
现在每条边只能走一次,给出一种走\(k\)次的方案,方案个数不能超过\(3000\),每个方案格式如下:
- \((cnt,s)\):即走\(cnt\)次\(s\)。
图大概如下所示:
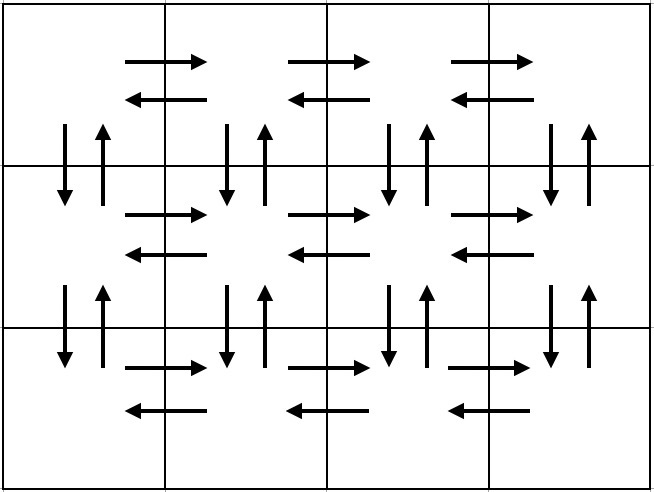
思路:
显然我们能走的步数越多越好,这个图存在很多种方案都可以把所有边走完,按照方案来贪心即可。
可能考虑的细节有点多。
Code
/*
* Author: heyuhhh
* Created Time: 2020/2/15 10:02:00
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
int n, m, k;
void run(){
if(4 * n * m - 2 * n - 2 * m < k) {
return void(cout << "NO" << '\n');
}
string s1 = "", s2 = "";
for(int i = 1; i < m; i++) s1 += "R";
for(int i = 1; i < m; i++) s1 += "L";
s1 += "D";
s2 += "R";
for(int i = 1; i < n; i++) s2 += "U";
for(int i = 1; i < n; i++) s2 += "D";
vector <pair<char, int>> ans;
string res = "";
for(int i = 1; i < n; i++) res += s1;
for(int i = 1; i < m; i++) res += s2;
for(int i = 1; i < m; i++) res += "L";
for(int i = 1; i < n; i++) res += "U";
for(int i = 0; i < k; i++) {
if(sz(ans) == 0 || ans.back().fi != res[i]) {
ans.push_back(MP(res[i], 1));
} else ++ans.back().se;
}
cout << "YES" << '\n';
cout << sz(ans) << '\n';
for(int i = 0; i < sz(ans); i++)
cout << ans[i].se << ' ' << ans[i].fi << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> n >> m >> k) run();
return 0;
}
E. Nanosoft
题意:
给出一个\(n*m,n,m\leq 500\)的矩阵,每个格子都有颜色,现在一共四种颜色\(R,G,Y,B\)。
如果一个正方形,其左上角的正方形全为\(R\),其右上角全为\(G\),其左下角全为\(Y\),其右下角全为\(B\),那么就称这个正方形合法。
比如以下的正方形是合法的:
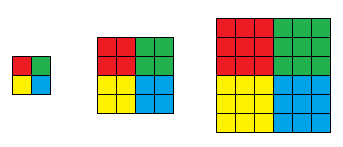
现在有\(q,q\leq 3\cdot 10^5\)次询问,每次询问给出一个矩形,回答这个矩形范围内最大的合法正方形的面积是多少。
思路:
我们可以直接通过二位前缀和预处理出以\((i,j)\)为左上顶点最大的合法正方形面积为多少。
对于每个询问,考虑直接枚举合法正方形的边长,看有多少个在范围之内,但这样显然时间复杂度不能承受。
考虑枚举合法正方形边长,然后在图中对应点打出标记,再求出二维前缀和。然后我们枚举所有询问,\(O(1)\)查询矩形范围内是否有该边长的合法正方形即可。
时间复杂度为\(O(n^3+nq)\),可以只用枚举边长的一半来减少常数。
还有一种做法就是处理出以一个点作为中心最大的合法正方形,那么我们只需要用一个数据结构查询矩形范围内最大值即可。
给出第一种的代码:
Code
/*
* Author: heyuhhh
* Created Time: 2020/2/15 10:49:29
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 500 + 5, M = 3e5 + 5;
int n, m, q;
ll sum[4][N][N], cnt[N][N];
char s[N][N];
int r1[M], r2[M], c1[M], c2[M];
int ans[M];
string ss = "RGYB";
void run(){
for(int i = 1; i <= n; i++) {
cin >> (s[i] + 1);
for(int j = 1; j <= m; j++) {
for(int k = 0; k < 4; k++) if(ss[k] == s[i][j]) {
sum[k][i][j] = 1;
}
}
}
for(int k = 0; k < 4; k++) {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
sum[k][i][j] += sum[k][i - 1][j];
}
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
sum[k][i][j] += sum[k][i][j - 1];
}
}
}
auto query = [&](int k, int r1, int c1, int r2, int c2) {
return sum[k][r2][c2] - sum[k][r2][c1 - 1] - sum[k][r1 - 1][c2] + sum[k][r1 - 1][c1 - 1];
};
auto query2 = [&](int r1, int c1, int r2, int c2) {
if(r2 < r1 || c2 < c1) return false;
return cnt[r2][c2] - cnt[r2][c1 - 1] - cnt[r1 - 1][c2] + cnt[r1 - 1][c1 - 1] > 0;
};
for(int i = 1; i <= q; i++) {
cin >> r1[i] >> c1[i] >> r2[i] >> c2[i];
}
for(int l = 1; l <= 250; l++) {
if(2 * l > n || 2 * l > m) break;
memset(cnt, 0, sizeof(cnt));
for(int i = 1; i <= n - 2 * l + 1; i++) {
for(int j = 1; j <= m - 2 * l + 1; j++) {
if(query(0, i, j, i + l - 1, j + l - 1) == l * l &&
query(1, i, j + l, i + l - 1, j + 2 * l - 1) == l * l &&
query(2, i + l, j, i + 2 * l - 1, j + l - 1) == l * l &&
query(3, i + l, j + l, i + 2 * l - 1, j + 2 * l - 1) == l * l
) cnt[i][j] = 1;
}
}
for(int i = 1; i <= n - 2 * l + 1; i++) {
for(int j = 1; j <= m - 2 * l + 1; j++) {
cnt[i][j] += cnt[i - 1][j];
}
}
for(int i = 1; i <= n - 2 * l + 1; i++) {
for(int j = 1; j <= m - 2 * l + 1; j++) {
cnt[i][j] += cnt[i][j - 1];
}
}
for(int i = 1; i <= q; i++) {
if(query2(r1[i], c1[i], r2[i] - 2 * l + 1, c2[i] - 2 * l + 1)) ans[i] = l;
}
}
for(int i = 1; i <= q; i++) cout << 4 * ans[i] * ans[i] << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> n >> m >> q) run();
return 0;
}
F. Super Jaber
题意:
又给出\(n*m,n,m\leq 1000\)的矩形,每个格子有一种颜色,颜色至多为\(k\)种,\(k\leq 40\)。
之后给出\(q,q\leq 10^5\)个询问,对于每个询问,回答从一个起点到达一个终点的最少花费。
移动规则为:当位于某个格子时,可以花费\(1\)向相邻的格子移动,或者花费\(1\)移动到任一同色的格子。
思路:
假设起点为\(s\),终点为\(t\),两点最短路为\(dis_{s,t}\)。
现有一个这样的性质:
- 若\(dis_{s,x}+dis_{y,t}=dis_{s,t},(x,y)\in edge\),那么\((x,y)\)这条边必然在最短路上。
对于这个题而言,我们分两种情况,第一种情况是不经过任何同色格子的跳跃,第二种情况就是会经过同色格子的跳跃。
第一种情况很好处理,对于第二种情况,我们直接枚举颜色\(i\),然后在所有的情况中取\(min\)即可。
那么我们需要处理出从某个颜色出发,到达其余所有点的最少花费。这个直接多源\(bfs\)即可。
代码如下:
Code
/*
* Author: heyuhhh
* Created Time: 2020/2/15 15:10:04
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1000 + 5, M = 45;
int n, m, k;
int a[N][N];
vector <pii> v[M];
int dis[M][N][N];
bool vis[M], chk[N][N];
void bfs(int col) {
queue <pii> q;
memset(dis[col], INF, sizeof(dis[col]));
memset(chk, 0, sizeof(chk));
memset(vis, 0, sizeof(vis));
for(auto it : v[col]) {
q.push(MP(it.fi, it.se));
dis[col][it.fi][it.se] = 0;
chk[it.fi][it.se] = true;
}
vis[col] = 1;
static const int dx[] = {-1, 1, 0, 0}, dy[] = {0, 0, -1, 1};
auto ok = [&](int x, int y) {
return x >= 1 && x <= n && y >= 1 && y <= m;
};
while(!q.empty()) {
int x = q.front().fi, y = q.front().se;
q.pop();
if(!vis[a[x][y]]) {
for(auto it : v[a[x][y]]) {
int nx = it.fi, ny = it.se;
if(dis[col][nx][ny] > dis[col][x][y] + 1) {
dis[col][nx][ny] = dis[col][x][y] + 1;
if(!chk[nx][ny]) {
chk[nx][ny] = true;
q.push(MP(nx, ny));
}
}
}
vis[a[x][y]] = 1;
}
for(int i = 0; i < 4; i++) {
int nx = x + dx[i], ny = y + dy[i];
if(ok(nx, ny) && dis[col][nx][ny] > dis[col][x][y] + 1) {
dis[col][nx][ny] = dis[col][x][y] + 1;
if(!chk[nx][ny]) {
chk[nx][ny] = true;
q.push(MP(nx, ny));
}
}
}
}
}
void run(){
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
cin >> a[i][j];
v[a[i][j]].push_back(MP(i, j));
}
}
for(int i = 1; i <= k; i++) {
bfs(i);
}
int q; cin >> q;
while(q--) {
int r1, r2, c1, c2; cin >> r1 >> c1 >> r2 >> c2;
int ans = abs(r1 - r2) + abs(c1 - c2);
for(int i = 1; i <= k; i++) {
ans = min(ans, dis[i][r1][c1] + dis[i][r2][c2] + 1);
}
cout << ans << '\n';
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> n >> m >> k) run();
return 0;
}
重要的是自信,一旦有了自信,人就会赢得一切。


