2020 CCPC Wannafly Winter Camp Day5
A. Alternative Accounts
题意:
现在有\(n\)个账号,举办\(k,k\leq 3\)场比赛。
现在每个人可能有多个账号,但每次只能用一个账号参加一场比赛。
现在给出\(k\)场比赛的参赛账号。
现在询问最少有多少人参加比赛。
思路:
分情况讨论即可。
我们可以直接认为\(k=3\)来分析:
- 若某个账号都出现在三场比赛中,那么直接让这个账号归属于某一人;
- 若某个账号出现在两场比赛中,那么这个账号可以和仅出现在另外一场比赛一次的账号进行匹配;不能匹配则不匹配;
- 若某个账号出现一次,现在剩下这些出现一次的账号可以互相匹配。
细节见代码,可能写得有点乱:
Code
#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
const int MAXN = 1e5+5,MAXM = 1e6+5,MOD = 998244353,INF = 0x3f3f3f3f,N=2e5;
const ll INFL = 0x3f3f3f3f3f3f3f3f;
const db eps = 1e-7;
#define lson o<<1,l,m
#define rson o<<1|1,m+1,r
#define mid l + ((r-l)>>1)
#define pii pair<int,int>
#define vii vector<pii>
#define vi vector<int>
#define x first
#define y second
using namespace std;
int n,k,sta[MAXN],cnt[10];
int main(){
ios::sync_with_stdio(false);cin.tie(0);
cin>>n>>k;
for(int i=1;i<=k;i++){
int m,x;
cin>>m;
while(m--){
cin>>x;
sta[x] |= 1<<(i-1);
}
}
for(int i=1;i<=n;i++){
if(sta[i])cnt[sta[i]]++;
}
if(k==1){
cout<<cnt[1]<<'\n';
}else if(k==2){
cout << cnt[1] + cnt[2] + cnt[3] - min(cnt[1],cnt[2])<<'\n';
}else{
int ans=0;
for(int i=1;i<8;i++)ans+=cnt[i];
int tmp;
tmp = min(cnt[3], cnt[4]);
cnt[3] -= tmp;
cnt[4] -= tmp;
ans -= tmp;
tmp = min(cnt[5],cnt[2]);
cnt[5] -= tmp;
cnt[2] -= tmp;
ans -= tmp;
tmp = min(cnt[6],cnt[1]);
cnt[6] -= tmp;
cnt[1] -= tmp;
ans -= tmp;
tmp = min(min(cnt[1],cnt[2]),cnt[4]);
cnt[1] -= tmp;
cnt[2] -= tmp;
cnt[4] -= tmp;
ans -= 2*tmp;
tmp = min(cnt[1], cnt[2]);
cnt[1] -= tmp;
cnt[2] -= tmp;
ans -= tmp;
tmp = min(cnt[1],cnt[4]);
cnt[1] -= tmp;
cnt[4] -= tmp;
ans -= tmp;
tmp = min(cnt[2],cnt[4]);
cnt[2] -= tmp;
cnt[4] -= tmp;
ans -= tmp;
cout<<ans<<'\n';
}
return 0;
}
B. Bitset Master
题意:
给出一颗树,每个点都有一个集合,初始\(S_u=\{u\}\)。
然后会执行若干次合并操作,每次会给出一条边,然后合并两端结点的集合。
最后对于每个点,输出有多少个集合包含他。
思路:
结合图论的一点思想,有多少个集合包含他,等价于从他能走到哪些集合。
现在将图反向,即等价于有多少个集合能走到他。
我们对于每个结点维护\(f_i\)表示有多少个集合能走到\(i\),最终就可以发现\(f_i\)即是最终集合的大小。
所以倒着来对每个集合求集合大小即可。
Code
/*
* Author: heyuhhh
* Created Time: 2020/2/12 15:22:56
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 5e5 + 5;
int n, m;
int a[N], b[N], c[N];
map <int, pii> mp[N];
int f[N], last[N];
void run(){
for(int i = 1; i <= n; i++) f[i] = 1;
for(int i = 1; i < n; i++) {
cin >> a[i] >> b[i];
}
for(int i = 1; i <= m; i++) cin >> c[i];
for(int i = m; i >= 1; i--) {
int u = a[c[i]], v = b[c[i]];
last[c[i]] = f[u] = f[v] = f[u] + f[v] - last[c[i]];
}
cout << f[1];
for(int i = 2; i <= n; i++) cout << " " << f[i];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> n >> m) run();
return 0;
}
C. Self-Adjusting Segment Tree
题意:
现在给出\(m\)个询问,每个询问为一段区间,区间范围为\([1,n]\)。
现在要在一棵自定义的树上面访问这些区间,这棵树每个叶子结点代表一个区间\([l,r]\),若区间长度大于\(1\),则存在一个\(k,l\leq k<r\),这个结点有两个儿子\([l,k],[k+1,r]\)。
比如这棵树可以为这样:
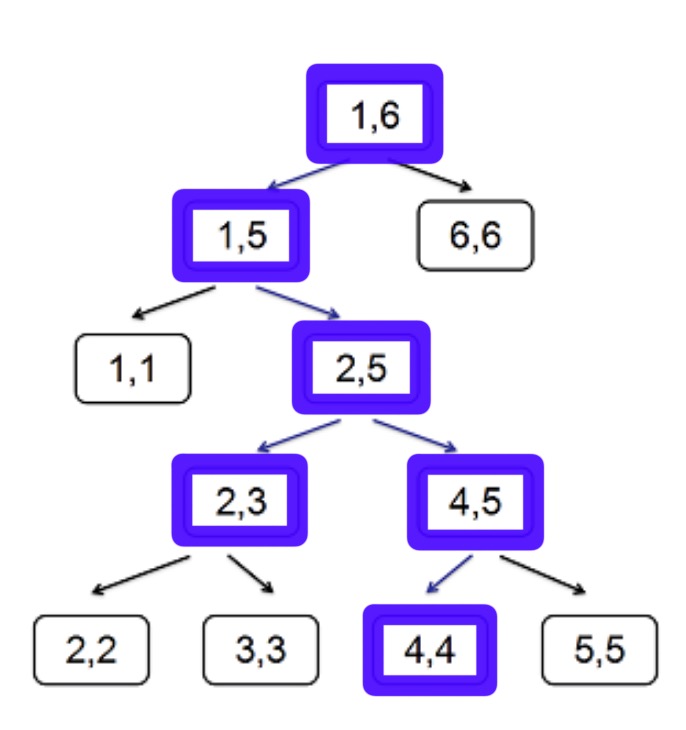
蓝色结点即为询问\([2,4]\)需要访问的区间。
现在请问在这样一棵树中询问所访问到结点的最少次数。
思路:
假设现在对于询问\([l,r]\),对于树上的结点\([l,r]\):
- 若\([l,r]\)与\([L,R]\)相交且\([l,r]\)不包含\([L,R]\),那么显然这个区间对访问次数的贡献为\(1\);
- 若\([l,r]\)包含\([L,R]\)且\(L\not ={R}\),这里的贡献为\(-1\);
- 若\([l,r]\)包含\([L,R]\)且\(L ={R}\),这里的贡献为\(1\);
第一个的贡献容易理解,主要就是后面两个贡献的处理。
在这样一棵树中有这样一个性质:
- 对于任意一个子树,其非叶子结点个数比叶子结点个数少\(1\)。
证明如下:
假设一个叶子结点代表的区间为\([L,R]\),那么每划分一次会产生两个结点,一共有\(R-L\)次划分,所以子树总结点个数为\(2\cdot (R-L)+1=(R-L+1)+R-L\)。因为叶子结点有\(R-L+1\)个,所以非叶子结点有\(R-L\)个。故该性质得证。
那么经过这样处理后,手模一下即可发现子树和的贡献为\(1\)。
那么对于每个区间\([L,R]\),我们可以事先预处理出其贡献,然后做个简单的区间\(dp\)进行合并即可。区间\(dp\)中两个区间的合并本质就是两个结点的合并。
代码如下:
Code
/*
* Author: heyuhhh
* Created Time: 2020/2/17 16:22:45
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 500 + 5, M = 2e5 + 5;
int n, m;
int a[N][N], b[N];
int dp[N][N];
void add(int r1, int c1, int r2, int c2, int v) {
a[r1][c1] += v;
a[r1][c2 + 1] -= v;
a[r2 + 1][c1] -= v;
a[r2 + 1][c2 + 1] += v;
}
void run(){
for(int i = 1; i <= m; i++) {
int l, r; cin >> l >> r;
add(1, l, r, n, 1);
add(l, l, r, r, -2);
b[l] += 2, b[r + 1] -= 2;
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
a[i][j] += a[i][j - 1];
}
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
a[i][j] += a[i - 1][j];
}
}
memset(dp, INF, sizeof(dp));
for(int i = 1; i <= n; i++) {
b[i] += b[i - 1];
a[i][i] += b[i];
dp[i][i] = a[i][i];
}
for(int l = 2; l <= n; l++) {
for(int i = 1; i <= n - l + 1; i++) {
int j = i + l - 1;
for(int k = i; k < j; k++) {
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j]);
}
dp[i][j] += a[i][j];
}
}
cout << dp[1][n] << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> n >> m) run();
return 0;
}
E. Matching Problem
题意:
给出两个序列\(a,b\),定义两个序列匹配当且仅当:
- 长度相等,且若\(a_i=a_j\),有\(b_i=b_j\)。
现在\(a\)的长度不超过\(300\),\(b\)的长度为\(4\)。问\(a\)有多少个子序列与\(b\)匹配。
思路:
直接暴力枚举子序列的前三个数,最后一个数直接预处理后缀即可。
Code
/*
* Author: heyuhhh
* Created Time: 2020/1/16 14:58:26
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 300 + 5;
int n;
int a[N];
int b[5], c[5];
int suf[N][N];
ll ans;
void gao(int pos, int cnt) {
if(pos >= n) return;
if(cnt == 3) {
int op = 0;
for(int i = 1; i <= 3; i++) {
if(b[4] == b[i]) op = i;
}
if(op == 0) {
ans += n - pos - suf[pos + 1][c[1]] - suf[pos + 1][c[2]] - suf[pos + 1][c[3]];
if(c[1] == c[2]) ans += suf[pos + 1][c[1]];
if(c[2] == c[3]) ans += suf[pos + 1][c[2]];
if(c[1] == c[3]) ans += suf[pos + 1][c[3]];
if(c[1] == c[2] && c[2] == c[3]) ans -= suf[pos + 1][c[1]];
} else {
ans += suf[pos + 1][c[op]];
}
return;
}
gao(pos + 1, cnt);
int x = a[pos + 1];
int ok = 1;
for(int i = 1; i <= cnt; i++) {
if((b[cnt + 1] == b[i]) != (x == c[i])) {
ok = 0;
}
}
if(ok) {
c[cnt + 1] = x;
gao(pos + 1, cnt + 1);
}
}
void run(){
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i <= 4; i++) cin >> b[i];
for(int i = n; i >= 1; i--) {
for(int j = 0; j < N; j++) suf[i][j] = suf[i + 1][j];
++suf[i][a[i]];
}
gao(0, 0);
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> n) run();
return 0;
}
F. Inversion Pairs
题意:
给出一个\(n,n\leq 10^7\),求出\(1\)~\(n\)的所有排列逆序对个数的\(k,k\leq 100\)次方之和。
思路:
首先容易想出来一个暴力\(dp\),\(dp_{i,j}\)表示当前考虑\(i\)个元素,逆序对个数为\(j\)的排列个数。那么转移为:
设\(f_i\)为\(i\)个元素时的答案,那么
然后。。然后。。
然后大力注意到\(\frac{f_i}{i!}\)或者\(\frac{f_i}{(i-2k)!}\)是个\(2k\)次多项式,然后直接上拉格朗日插值即可。
Code
/*
* Author: heyuhhh
* Created Time: 2020/2/12 17:03:35
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#include <assert.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 205, M = 40000 + 5, MOD = 1e9 + 7;
int n, k;
int fac[N], inv[N];
int qpow(ll a, ll b) {
ll res = 1;
while(b) {
if(b & 1) res = res * a % MOD;
a = a * a % MOD;
b >>= 1;
}
return res;
}
int val[M];
int dp[N][M], f[N], g[M];
struct Lagrange {
static const int SIZE = N;
ll f[SIZE], fac[SIZE], inv[SIZE], pre[SIZE], suf[SIZE];
int n;
inline void add(ll &x, int y) {
x += y;
if(x >= MOD) x -= MOD;
}
void init(int _n, int* _f) {
n = _n;
fac[0] = 1;
for (int i = 1; i < SIZE; ++i) fac[i] = fac[i - 1] * i % MOD;
inv[SIZE - 1] = qpow(fac[SIZE - 1], MOD - 2);
for (int i = SIZE - 1; i >= 1; --i) inv[i - 1] = inv[i] * i % MOD;
//设置f初值,可以根据需要修改
for (int i = 0; i <= n; ++i)
f[i] = _f[i];
}
ll calc(ll x) {
if (x <= n) return f[x];
pre[0] = x % MOD;
for (int i = 1; i <= n; ++i) pre[i] = pre[i - 1] * ((x - i) % MOD) % MOD;
suf[n] = (x - n) % MOD;
for (int i = n - 1; i >= 0; --i) suf[i] = suf[i + 1] * ((x - i) % MOD) % MOD;
ll res = 0;
for (int i = 0; i <= n; ++i) {
ll tmp = f[i] * inv[n - i] % MOD * inv[i] % MOD;
if (i) tmp = tmp * pre[i - 1] % MOD;
if (i < n) tmp = tmp * suf[i + 1] % MOD;
if ((n - i) & 1) tmp = MOD - tmp;
add(res, tmp);
}
return res;
}
}lagrange;
void run(){
fac[0] = 1;
for(int i = 1; i < N; i++) fac[i] = 1ll * fac[i - 1] * i % MOD;
inv[N - 1] = qpow(fac[N - 1], MOD - 2);
for(int i = N - 2; i >= 0; i--) inv[i] = 1ll * inv[i + 1] * (i + 1) % MOD;
for(int i = 0; i < M; i++) val[i] = qpow(i, k);
g[0] = dp[0][0] = 1;
for(int i = 1; i <= 2 * k; i++) {
for(int j = 0; j <= (i - 1) * i / 2; j++) {
if(j - i >= 0) dp[i][j] = (g[j] - g[j - i] + MOD) % MOD;
else dp[i][j] = g[j];
}
g[0] = dp[i][0];
for(int j = 1; j < M; j++) {
g[j] = (g[j - 1] + dp[i][j]) % MOD;
}
}
for(int i = 1; i <= 2 * k; i++) {
for(int j = 0; j <= i * (i - 1) / 2; j++) {
f[i] = (f[i] + 1ll * dp[i][j] * val[j] % MOD) % MOD;
}
}
if(n <= 2 * k) {
cout << f[n];
return;
}
for(int i = 1; i <= 2 * k; i++) {
f[i] = 1ll * f[i] * inv[i] % MOD;
}
lagrange.init(2 * k, f);
int res = lagrange.calc(n);
for(int i = 2; i <= n; i++) res = 1ll * res * i % MOD;
cout << res;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> n >> k) run();
return 0;
}
G. Cryptographically Secure Pseudorandom Number Generator
题意:
给出一个素数\(p\),寻找所有的\(x\)满足:
\(f(x)\)满足\(x\cdot f(x)\equiv 1 (mod\ p)\)。
思路:
打个表发现具有对称关系。
然后猜一猜,可能只会枚举到根号,直接暴力过去就行了。。。
Code
/*
* Author: heyuhhh
* Created Time: 2020/1/16 21:33:24
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e6 + 5;
int MOD;
int inv[N];
void run(){
cin >> MOD;
inv[0] = inv[1] = 1;
vector <pii> ans;
int Min = INF;
for(int i = 2; i < MOD; i++) {
inv[i] = 1ll * (MOD - MOD / i) * inv[MOD % i] % MOD;
if(inv[i] <= Min) {
if(i > inv[i]) break;
Min = inv[i];
ans.push_back(MP(i, inv[i]));
}
}
vector <pii> res = ans;
reverse(all(res));
for(auto it : res) if(it.fi != it.se) ans.push_back(MP(it.se, it.fi));
cout << sz(ans) << '\n';
for(auto it : ans) cout << it.fi << ' ' << it.se << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
int T; cin >> T;
while(T--) run();
return 0;
}
H. Geometry PTSD
题意:
空间直角坐标系中找到三个点\(A,B,C\),使得\((0,0)\)到平面\(ACB\)的距离不超过\(10^{-18}\)。
同时要满足限制:\(min(|AB|,|AC|,|BC|)\geq 1.7\)。
思路:
满足限制的话我们考虑在单位球上选择三个点即可。
在单位球上找一个过圆心的平面,然后施加扰动来check。
check方法:
我们知道体积为\(\frac{dS}{3}\),\(S\)底面面积可以直接估算,同时体积可以用行列式算出来,那么就可以直接把\(d\)求出来。
大致就是这样。
Code
/*
* Author: heyuhhh
* Created Time: 2020/2/12 11:47:38
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
void run(){
cout << "999999 1000000 0" << '\n';
cout << "-999998 0 999999" << '\n';
cout << "0 -999998 -999997" << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
run();
return 0;
}
I. Practice for KD Tree
题意:
给出一个\(n\cdot n,n\leq 2000\)的矩阵,然后给出\(m_1,m_2\),分别代表两种操作的数量。
第一种操作,对于\((x_1,y_1),(x_2,y_2),x_1\leq x_2,y_1\leq y_2\)的矩阵内部所有元素都加上\(w\)。
第二种操作,询问矩阵元素最大值。
注意是先给完第一种操作,然后再执行第二种操作。
思路:
因为两种操作独立,所以我们可以分开考虑。
对于第一种操作,直接二维前缀和即可解决。
接下来主要考虑第二种操作。
因为\(n\)不大,所以我们直接可以通过二位线段树来解决,建树的时间复杂度为\(O(n^2logn)\),单次操作的时间复杂度为\(O(log^2n)\)。
一开始第二维我是直接动态开点,后来发现空间会多个倍数。如果直接用结构题的话,空间刚好为\((4n)^2\),并且还有个什么内存对齐,比较节约空间。
代码如下:
Code
/*
* Author: heyuhhh
* Created Time: 2020/2/11 15:41:25
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 2000 + 5;
int n, m1, m2;
int x[2], y[2];
ll a[N][N];
struct yTree {
ll maxv[N << 2];
void build(int o, int l, int r, int L, int R) {
if(l == r) {
for(int i = L; i <= R; i++) {
maxv[o] = max(maxv[o], a[i][l]);
}
return ;
}
int mid = (l + r) >> 1;
build(o << 1, l, mid, L, R);
build(o << 1|1, mid + 1, r, L, R);
maxv[o] = max(maxv[o << 1], maxv[o << 1|1]);
}
ll query(int o, int l, int r, int L, int R) {
if(L <= l && r <= R) {
return maxv[o];
}
ll res = 0; int mid = (l + r) >> 1;
if(L <= mid) res = query(o << 1, l, mid, L, R);
if(R > mid) res = max(res, query(o << 1|1, mid + 1, r, L, R));
return res;
}
};
struct xTree {
yTree t[N << 2];
void build(int o, int l, int r) {
t[o].build(1, 1, n, l, r);
if(l == r) return;
int mid = (l + r) >> 1;
build(o << 1, l, mid);
build(o << 1|1, mid + 1, r);
}
ll query(int o, int l, int r, int L, int R) {
if(L <= l && r <= R) {
return t[o].query(1, 1, n, y[0], y[1]);
}
ll res = 0; int mid = (l + r) >> 1;
if(L <= mid) res = query(o << 1, l, mid, L, R);
if(R > mid) res = max(res, query(o << 1|1, mid + 1, r, L, R));
return res;
}
}X;
void run() {
for(int i = 1; i <= m1; i++) {
int w;
cin >> x[0] >> y[0] >> x[1] >> y[1] >> w;
a[x[0]][y[0]] += w;
a[x[1] + 1][y[1] + 1] += w;
a[x[1] + 1][y[0]] -= w;
a[x[0]][y[1] + 1] -= w;
}
for(int j = 1; j <= n; j++) {
for(int i = 1; i <= n; i++) {
a[i][j] += a[i - 1][j];
}
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
a[i][j] += a[i][j - 1];
}
}
X.build(1, 1, n);
for(int i = 1; i <= m2; i++) {
cin >> x[0] >> y[0] >> x[1] >> y[1];
ll ans = X.query(1, 1, n, x[0], x[1]);
cout << ans << '\n';
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> n >> m1 >> m2) run();
return 0;
}
J. Xor on Figures
题意:
给出一个\(2^k\cdot 2^k\)的全零矩阵\(M\)。
然后给出\(2^k\cdot 2^k\)的\(01\)矩阵\(F\),现在可以将\(F\)的左上角置于\(M\)的任一位置(超出部分就循环,\(2^k\)的下一个就是\(1\)),然后相应位置相异或。
现在可以执行任意次以上操作:将\(F\)放于某个位置,执行对应的异或操作。
问最后不同的\(M\)有多少个。
思路:
通过\(2^{2k}\)枚举放置顶点,并且枚举每个位置得到一次操作后得到的矩形。
因为现在可以执行任意次操作,并且求最后不同的矩形个数。
那么我们将每次操作过后得到的矩形拼接为一个\(01\)串,然后考虑求出其秩的个数\(r\),那么答案就为\(2^r\)。
直接用线性基来求,时间复杂度为\(O(2^{6k})\),两个串相异或时容易想到用\(bitset\)优化,所以总的时间复杂度为\(O(2^{6k}/w)\)。
代码如下:
Code
/*
* Author: heyuhhh
* Created Time: 2020/2/12 11:01:42
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <bitset>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1024 + 5, M = 35, MOD = 1e9 + 7;
int qpow(ll a, ll b) {
ll res = 1;
while(b) {
if(b & 1) res = res * a % MOD;
a = a * a % MOD;
b >>= 1;
}
return res;
}
int k;
bool chk[N];
bitset <N> a[N], p[N];
char f[M][M];
int id(int x, int y) {
return (x - 1) * (1 << k) + y;
}
void run(){
for(int i = 1; i <= 1 << k; i++) {
cin >> (f[i] + 1);
}
int t = 1 << k;
for(int x = 1; x <= t; x++) {
for(int y = 1; y <= t; y++) {
int now = id(x, y);
for(int i = 1; i <= t; i++) {
for(int j = 1; j <= t; j++) {
if(f[i][j] == '1') {
a[now][id((x + i - 1) % t + 1, (y + j - 1) % t + 1)] = 1;
}
}
}
}
}
int s = 0;
for(int i = 1; i <= t * t; i++) {
for(int j = t * t; j >= 1; j--) if(a[i][j]){
if(!chk[j]) {
chk[j] = true;
p[j] = a[i];
++s;
break;
}
a[i] = a[i] ^ p[j];
}
}
int ans = qpow(2, s);
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> k) run();
return 0;
}
重要的是自信,一旦有了自信,人就会赢得一切。


