Codeforces Round #603 (Div. 2)
感觉脑子还是转得太慢了QAQ,一些问题老是想得很慢。。。
A. Sweet Problem
签到。
Code
/*
* Author: heyuhhh
* Created Time: 2019/11/29 22:36:19
*/
#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
int a[3];
void run(){
for(int i = 0; i < 3; i++) cin >> a[i];
sort(a, a + 3);
int ans = a[0];
int d = a[2] - a[1];
if(d >= ans) ans += a[1];
else {
ans += a[1] - (ans - d + 1) / 2;
}
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
int T; cin >> T;
while(T--) run();
return 0;
}
B. PIN Codes
注意到\(n\)很小,不超过\(10\),那么就直接暴力改变就行。
可以用一个\(map\)记录一下。
Code
/*
* Author: heyuhhh
* Created Time: 2019/11/29 22:46:29
*/
#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
int n;
map <string, int> mp;
string s[20];
void run(){
cin >> n;
mp.clear();
for(int i = 1; i <= n; i++) {
cin >> s[i];
mp[s[i]]++;
}
int ans = n - mp.size();
vector <string> res;
for(int i = 1; i <= n; i++) {
if(mp[s[i]] > 1) {
string t = s[i];
int f = 1;
for(int j = 0; f && j < 4; j++) {
char pre = t[j];
for(int k = 0; k < 10; k++) {
t[j] = (k + '0');
if(mp.find(t) == mp.end()) {
mp[t] = 1;
f = 0;
break;
}
if(k == 9) t[j] = pre;
}
}
res.push_back(t);
--mp[s[i]];
} else res.push_back(s[i]);
}
cout << ans << '\n';
for(auto it : res) cout << it << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
int T; cin >> T;
while(T--) run();
return 0;
}
C. Everyone is a Winner!
数论分块模板题。
Code
/*
* Author: heyuhhh
* Created Time: 2019/11/29 22:58:21
*/
#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e5 + 5;
void run(){
vector <int> ans;
int n;
cin >> n;
for(int l = 1, r; l <= n; l = r + 1) {
r = n / (n / l);
ans.push_back(n / l);
}
ans.push_back(0);
sort(all(ans));
cout << sz(ans) << '\n';
for(auto it : ans) cout << it << ' ';
cout << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
int T; cin >> T;
while(T--) run();
return 0;
}
D. Secret Passwords
题意:
现在给出\(n\)个长度最多为\(50\)的字符串,定义两个字符串等价为:
- 若\(A,B\)等价,那么在\(A,B\)中至少存在一个字符相同;
- 若\(A,C\)等价以及\(B,C\)等价,那么有\(A,B\)等价。
问最后所有的字符串可以划分为多少个等价类。
思路:
一开始以为是\(bitset\),后来发现是个并查集模板题= =
显然,问题中第一个描述:我们可以直接枚举每个字符,并将含有其的字符串合并在一起;对于第二个描述,显然可以发现第一步已经处理了这个问题,所有符合条件的已经自然地并在了一起。
那么并查集维护一下合并关系就行了。
Code
/*
* Author: heyuhhh
* Created Time: 2019/11/29 23:09:50
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 2e5 + 5;
char s[N][55];
int n;
int f[N];
int find(int x) {
return f[x] == x ? f[x] : f[x] = find(f[x]);
}
void Union(int x, int y) {
int fx = find(x), fy = find(y);
if(fx != fy) {
f[fx] = fy;
}
}
void run(){
vector <int> v[26];
for(int i = 1; i <= n; i++) {
cin >> (s[i] + 1);
int len = strlen(s[i] + 1);
for(int j = 1; j <= len; j++) {
v[s[i][j] - 'a'].push_back(i);
}
}
for(int i = 1; i <= n; i++) f[i] = i;
for(int i = 0; i < 26; i++) if(sz(v[i]) > 0) {
int x = v[i][0];
for(int j = 1; j < sz(v[i]); j++) {
int y = v[i][j];
Union(x, y);
}
}
int ans = 0;
for(int i = 1; i <= n; i++) if(f[i] == i) ++ans;
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> n) run();
return 0;
}
E. Editor
题意:
现在有一个打字机,一开始当前行为空白。开始时光标位于第\(1\)个位置,然后输入一个字符串为执行相关的指令,指令有:
- R:光标向右移动一个位置;
- L:若光标大于第\(1\)个位置,则向左移动一个位置;
- 其它字符:打印相关字符到当前位置,并对之前的字符进行覆盖。
每一次指令结束过后,你需要输出一个答案,该答案为:
- 若当前串为一个合法的括号序列,那么输出括号嵌套的最大层数,比如\("(sd)(\ ()dd)"\)则输出\(2\);
- 否则输出\(-1\)。
思路:
我一开始说的就是这个题,比赛的时候感觉好多东西都没想清楚...
感觉脑子转的快的话挺好想的(马后炮?)
首先来搞清楚我们要求出答案,需要满足什么关系:
- 对于合法序列来说:要满足对于任意一个\(i\),有\(sum[i]\geq 0\)。这里的\(sum[i]\)算的是我们将\((\)看作\(1\),将\()\)看作\(-1\),然后求的一个前缀和。并且还要满足\(sum[n]=0\),这个比较显然。
- 那么最大层数呢?
- 简单思考可以发现,最大层数就是要求这样一个东西\(max\{sum[i]\},1\leq i\leq n\)。
怎么得到答案清楚了,接下来就是分析操作对答案的影响:
- 左右移动光标:这个很简单,直接移动即可。
- 打印字符:因为我们的\(sum[i]\)是一个前缀的结果,那么显然我们对某一位进行修改,影响的是一个后缀,那么其实每次操作都是对一个后缀的影响。
- 所以直接考虑线段树,每个位置表示\(sum[i]\),并且维护一个最小值和最大值。对于修改操作,则是在线段树上的一个区间修改;对于回答,直接找相关值就行了。
剩下的就是一点点细节。
详见代码:
Code
/*
* Author: heyuhhh
* Created Time: 2019/11/30 9:57:38
*/
#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 1e6 + 5;
int n;
char s[N];
int maxv[N << 2], minv[N << 2], lz[N << 2];
void push_up(int o) {
minv[o] = min(minv[o << 1], minv[o << 1|1]);
maxv[o] = max(maxv[o << 1], maxv[o << 1|1]);
}
void push_down(int o, int l, int r) {
if(lz[o] != 0) {
int mid = (l + r) >> 1;
maxv[o << 1] += lz[o];
minv[o << 1] += lz[o];
maxv[o << 1|1] += lz[o];
minv[o << 1|1] += lz[o];
lz[o << 1] += lz[o];
lz[o << 1|1] += lz[o];
lz[o] = 0;
}
}
void build(int o, int l, int r) {
maxv[o] = minv[o] = 0;
if(l == r) return;
int mid = (l + r) >> 1;
if(l <= mid) build(o << 1, l, mid);
if(r > mid) build(o << 1|1, mid + 1, r);
}
void upd(int o, int l, int r, int L, int R, int v) {
if(L <= l && r <= R) {
lz[o] += v;
maxv[o] += v; minv[o] += v;
return;
}
push_down(o, l, r);
int mid = (l + r) >> 1;
if(L <= mid) upd(o << 1, l, mid, L, R, v);
if(R > mid) upd(o << 1|1, mid + 1, r, L, R, v);
push_up(o);
}
int a[N];
void run(){
cin >> (s + 1);
build(1, 1, n);
int p = 1;
int sum = 0;
for(int i = 1; i <= n; i++) {
if(s[i] == '(') {
if(a[p] == 0) upd(1, 1, n, p, n, 1), ++sum;
else if(a[p] == -1) {
upd(1, 1, n, p, n, 2), sum += 2;
}
a[p] = 1;
} else if(s[i] == ')') {
if(a[p] == 0) upd(1, 1, n, p, n, -1), --sum;
else if(a[p] == 1) {
upd(1, 1, n, p, n, -2), sum -= 2;
}
a[p] = -1;
} else if(s[i] == 'R') {
++p;
} else if(s[i] == 'L') {
if(p > 1) --p;
} else {
if(a[p] == 1) upd(1, 1, n, p, n, -1), --sum;
else if(a[p] == -1) upd(1, 1, n, p, n, 1), ++sum;
a[p] = 0;
}
if(sum == 0 && minv[1] >= 0) {
cout << maxv[1];
} else cout << -1;
cout << " \n"[i == n];
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> n) run();
return 0;
}
F. Economic Difficulties
题意:
给出两棵有根树树上下拼接,保证其叶子个数相同。两棵树对应叶子中间有个电机,每棵树的根可以给叶子结点供电,叶子结点可以给电机供电。
大概像这个样子:
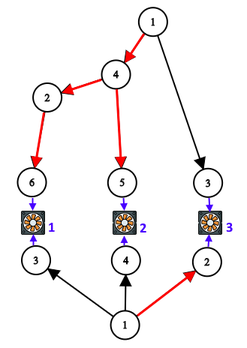
现在要删掉最多的边,同时保证每个电机都有电。
问最多能删掉多少边?
思路:
分析删除一颗数的某个叶子结点,最多能删掉多少边。
显然,如果我们知道了上一次保留的结点\(last\),假设当前结点为\(now\),那么我们最多能删边的数量为:\(deep[now]-max(lca(last,now),lca(now,now+1))\)。
因为我们每次删是尽可能往多的删,那么必然会受到上一次保留的结点的限制(若保留一个结点,那么根到其的链也会保留);同时,还要受到下一个结点的限制(默认下一次是保留的)。
那么根据这个直接\(dp\)就行,枚举下一个是哪颗子数删,然后转移一下即可。
代码如下:
Code
/*
* Author: heyuhhh
* Created Time: 2019/12/2 14:42:31
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 2005;
int tot;
struct LCA {
int n;
vector <int> g[N];
int a[N], deep[N], f[N][12];
void scan() {
cin >> n;
for(int i = 2; i <= n; i++) {
int p; cin >> p;
g[p].push_back(i);
}
for(int i = 1; i <= tot; i++) {
cin >> a[i];
}
}
void dfs(int u, int d) {
deep[u] = d;
for(int i = 1; i < 12; i++) {
f[u][i] = f[f[u][i - 1]][i - 1];
}
for(auto v : g[u]) {
f[v][0] = u;
dfs(v, d + 1);
}
}
int lca(int x, int y) {
if(!x || !y) return 1;
if(deep[x] < deep[y]) swap(x, y);
for(int i = 11; i >= 0; i--) {
if(deep[f[x][i]] >= deep[y]) x = f[x][i];
}
if(x == y) return deep[x];
for(int i = 11; i >= 0; i--) {
if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
}
return deep[f[x][0]];
}
}A, B;
int dp[N][N];
void run(){
A.scan(); B.scan();
A.dfs(1, 1); B.dfs(1, 1);
dp[0][1] = A.deep[A.a[1]] - A.lca(A.a[1], A.a[2]);
dp[1][0] = B.deep[B.a[1]] - B.lca(B.a[1], B.a[2]);
int ans = 0;
for(int i = 0; i <= tot; i++) {
for(int j = 0; j <= tot; j++) {
if(i == j) continue;
int Max = max(i, j);
if(Max == tot) {
ans = max(ans, dp[i][j]);
continue;
}
dp[i][Max + 1] = max(dp[i][Max + 1], dp[i][j] + A.deep[A.a[Max + 1]] - max(A.lca(A.a[i], A.a[Max + 1]), A.lca(A.a[Max + 1], A.a[Max + 2])));
dp[Max + 1][j] = max(dp[Max + 1][j], dp[i][j] + B.deep[B.a[Max + 1]] - max(B.lca(B.a[j], B.a[Max + 1]), B.lca(B.a[Max + 1], B.a[Max + 2])));
}
}
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> tot) run();
return 0;
}
另外还有一种比较巧妙的方法,给大家推荐卿学姐的视频题解(感谢卿学姐orz)
就是如果我们知道删除某个区间的最大代价,那么问题就等价于一个类似于区间覆盖的问题,到时候直接一维\(dp\)就行了。
怎么求这个代价呢。直接\(dfs\)求就行了,毕竟空间复杂度\(O(n^2)\)可以接受,用一个数组\(val[l,r]\)表示不给\([l,r]\)供电最多能删几条边,更新的时候维护一下子树\(sz\)即可(任意一个区间都可以等价于某颗子树的叶子节点)。
细节详见代码:
Code
/*
* Author: heyuhhh
* Created Time: 2019/12/2 18:46:13
*/
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
#define INF 0x3f3f3f3f
#define Local
#ifdef Local
#define dbg(args...) do { cout << #args << " -> "; err(args); } while (0)
void err() { std::cout << '\n'; }
template<typename T, typename...Args>
void err(T a, Args...args) { std::cout << a << ' '; err(args...); }
#else
#define dbg(...)
#endif
void pt() {std::cout << '\n'; }
template<typename T, typename...Args>
void pt(T a, Args...args) {std::cout << a << ' '; pt(args...); }
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
//head
const int N = 2005;
int n;
int dp[N];
int l[2][N], r[2][N], sz[2][N];
int val[2][N][N];
vector <int> g[2][N];
void dfs(int T, int u) {
if(u != 1) sz[T][u] = 1;
for(auto v : g[T][u]) {
dfs(T, v);
l[T][u] = min(l[T][u], l[T][v]);
r[T][u] = max(r[T][u], r[T][v]);
sz[T][u] += sz[T][v];
}
val[T][l[T][u]][r[T][u]] = max(val[T][l[T][u]][r[T][u]], sz[T][u]);
}
void run(){
memset(l, INF, sizeof(l));
for(int k = 0; k < 2; k++) {
int a; cin >> a;
for(int i = 2; i <= a; i++) {
int p; cin >> p;
g[k][p].push_back(i);
}
for(int i = 1; i <= n; i++) {
int x; cin >> x;
l[k][x] = i, r[k][x] = i;
}
dfs(k, 1);
}
for(int i = 1; i <= n; i++) {
for(int j = 0; j < i; j++) {
dp[i] = max(dp[i], dp[j] + max(val[0][j + 1][i], val[1][j + 1][i]));
}
}
cout << dp[n] << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cout << fixed << setprecision(20);
while(cin >> n) run();
return 0;
}
发现最近写题解越来越啰嗦了qaq。
重要的是自信,一旦有了自信,人就会赢得一切。


