POJ2699:The Maximum Number of Strong Kings(枚举+贪心+最大流)

The Maximum Number of Strong Kings

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 2488		Accepted: 1131

题目链接：http://poj.org/problem?id=2699

Description:

A tournament can be represented by a complete graph in which each vertex denotes a player and a directed edge is from vertex x to vertex y if player x beats player y. For a player x in a tournament T, the score of x is the number of players beaten by x. The score sequence of T, denoted by S(T) = (s1, s2, . . . , sn), is a non-decreasing list of the scores of all the players in T. It can be proved that S(T) = (s1, s2, . . . , sn) is a score sequence of T if and only if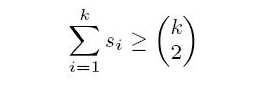 
for k = 1, 2, . . . , n and equality holds when k = n. A player x in a tournament is a strong king if and only if x beats all of the players whose scores are greater than the score of x. For a score sequence S, we say that a tournament T realizes S if S(T) = S. In particular, T is a heavy tournament realizing S if T has the maximum number of strong kings among all tournaments realizing S. For example, see T2 in Figure 1. Player a is a strong king since the score of player a is the largest score in the tournament. Player b is also a strong king since player b beats player a who is the only player having a score larger than player b. However, players c, d and e are not strong kings since they do not beat all of the players having larger scores. 
The purpose of this problem is to find the maximum number of strong kings in a heavy tournament after a score sequence is given. For example,Figure 1 depicts two possible tournaments on five players with the same score sequence (1, 2, 2, 2, 3). We can see that there are at most two strong kings in any tournament with the score sequence (1, 2, 2, 2, 3) since the player with score 3 can be beaten by only one other player. We can also see that T2 contains two strong kings a and b. Thus, T2 is one of heavy tournaments. However, T1 is not a heavy tournament since there is only one strong king in T1. Therefore, the answer of this example is 2.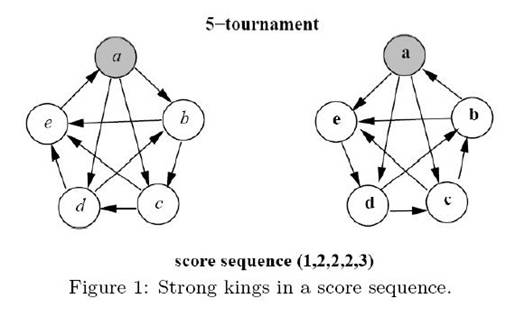 
 

Input:

The first line of the input file contains an integer m, m <= 10, which represents the number of test cases. The following m lines contain m score sequences in which each line contains a score sequence. Note that each score sequence contains at most ten scores.

Output:

The maximum number of strong kings for each test case line by line.

Sample Input:

5
1 2 2 2 3
1 1 3 4 4 4 4
3 3 4 4 4 4 5 6 6 6
0 3 4 4 4 5 5 5 6
0 3 3 3 3 3

Sample Output:

2
4
5
3
5

题意：

多组数据，然后对于每组数据给出每个人击败的人数，为最多有多少人是强者。

强者的定义为：得到的分数最多 or 击败所有分数比他高的人。这里每击败一个人都可以得一分。

 

题解：

这题orz...没有想出来。但最后看了题解后发现就是个公平分配问题。

我们建图时比赛在左边，人在右边。每场比赛连两个人，代表这两个人在比赛，然后每场比赛只会分配1的流出去，代表哪个人获胜。

这就是我们建图的大体思路。

由于人数很少，所以我们可以枚举来确定强者，那么怎么确定呢，直接二进制表示的话复杂度太高。

通过证明可以发现，分数越高的人越有可能成为强者，简要证明过程如下：

假设分数为: ...i j k ......，这里i和k时强者，而j不是。如果i是强者，那么说明i打败了后面的所有人，而j不是强者，则说明他可能输给了后面的某几个人。

因为j的分数比i的分数高，说明j多欺负了几个弱者。那么现在我们让j赢回高分的人，让i去赢前面多欺负的那几个人，此时i可能会输给比他强的人，此时满足赢的数量和之前一样。相当于换了人去欺负那些弱者。这样j也可以变为强者了。

以上就是简略的一个证明，只要保证每个人的分数不变就ok。

然后我们从分数大开始枚举，在建图时，源点连接比赛，容量为1；人连接汇点，容量为他能赢的最多次数。

比赛连接两个人时，如果一个人是强者并且另一个人分数比他高，那么只能强者赢；否则哪个赢都可以。对赢的那个人连接容量为1的边。

最后跑个最大流看看比赛能否比完就行了（我这里是通过是否每个人的分数能够符合题意来判断的）。

 

代码如下:

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <queue>
#define s 0
#define t 200
#define INF 0x3f3f3f3f
#define st n*(n-1)/2
using namespace std;
typedef long long ll;
const int N = 1005;
int T;
char str[N];
int a[N],vis[N],head[N],d[N];
int ans,tot,mx,n,sum;
struct Edge{
    int v,c,next;
}e[N*N];
void adde(int u,int v,int c){
    e[tot].v=v;e[tot].next=head[u];e[tot].c=c;head[u]=tot++;
    e[tot].v=u;e[tot].next=head[v];e[tot].c=0;head[v]=tot++;
}
void build(){
    memset(head,-1,sizeof(head));tot=0;
    for(int i=1;i<=st;i++) adde(s,i,1);
    int fir = st+1,last = st+2;
    for(int i=1;i<=st;i++){
        if(vis[fir]&&a[last-st]>a[fir-st]){
            adde(i,fir,1);adde(i,last,0);
        }else if(vis[last]&&a[last-st]<a[fir-st]){
            adde(i,fir,0);adde(i,last,1);
        }else{
            adde(i,fir,1);adde(i,last,1);
        }
        last++;
        if(last>st+n){
            fir++;last=fir+1;
        }
    }
    for(int i=st+1;i<=st+n;i++) adde(i,t,a[i-st]);
}
bool bfs(int S,int T){
    memset(d,0,sizeof(d));d[S]=1;
    queue <int > q;q.push(S);
    while(!q.empty()){
        int u=q.front();q.pop();
        for(int i=head[u];i!=-1;i=e[i].next){
            int v=e[i].v;
            if(!d[v] && e[i].c>0){
                d[v]=d[u]+1;
                q.push(v);
            }
        }
    }
    return d[T]!=0;
}
int dfs(int S,int a){
    int flow=0,f;
    if(S==t || a==0) return a;
    for(int i=head[S];i!=-1;i=e[i].next){
        int v=e[i].v;
        if(d[v]!=d[S]+1) continue ;
        f=dfs(v,min(a,e[i].c));
        if(f){
            e[i].c-=f;
            e[i^1].c+=f;
            flow+=f;
            a-=f;
            if(a==0) break;
        }
    }
    if(!flow) d[S]=-1;
    return flow;
}
int Dinic(){
    int max_flow=0;
    while(bfs(0,t)) max_flow+=dfs(0,INF);
    return max_flow;
}
int main(){
    cin>>T;
    getchar();
    while(T--){
        memset(vis,0,sizeof(vis));
        gets(str);
        mx=n=sum=0;ans=-1;
        int len = strlen(str);
        for(int i=0;i<len;i++)
            if(str[i]<='9' && str[i]>='0')
                a[++n]=str[i]-'0',mx = max(mx,a[n]),sum+=a[n];
        for(int i=n;i>=1;i--){
            if(a[i]==mx) continue ;
            vis[i+st]=1;
            build();
            int max_flow=Dinic();
            if(max_flow<sum){
                ans=n-i;
                break ;
            }
        }
        if(ans==-1) ans=n;
        cout<<ans<<endl;  
    }
    return 0;
}