POJ3585:Accumulation Degree(换根树形dp)

Accumulation Degree

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 3425		Accepted: 859

题目链接：http://poj.org/problem?id=3585

Description:

Trees are an important component of the natural landscape because of their prevention of erosion and the provision of a specific ather-sheltered ecosystem in and under their foliage. Trees have also been found to play an important role in producing oxygen and reducing carbon dioxide in the atmosphere, as well as moderating ground temperatures. They are also significant elements in landscaping and agriculture, both for their aesthetic appeal and their orchard crops (such as apples). Wood from trees is a common building material.

Trees also play an intimate role in many of the world's mythologies. Many scholars are interested in finding peculiar properties about trees, such as the center of a tree, tree counting, tree coloring. A(x) is one of such properties.

A(x) (accumulation degree of node x) is defined as follows:

 

1. Each edge of the tree has an positive capacity.
2. The nodes with degree of one in the tree are named terminals.
3. The flow of each edge can't exceed its capacity.
4. A(x) is the maximal flow that node x can flow to other terminal nodes.

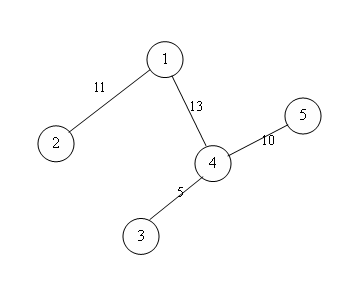
Since it may be hard to understand the definition, an example is showed below:

 

A(1)=11+5+8=24
Details:	1->2	11
	1->4->3	5
	1->4->5	8(since 1->4 has capacity of 13)
A(2)=5+6=11
Details:	2->1->4->3	5
	2->1->4->5	6
A(3)=5
Details:	3->4->5	5
A(4)=11+5+10=26
Details:	4->1->2	11
	4->3	5
	4->5	10
A(5)=10
Details:	5->4->1->2	10

The accumulation degree of a tree is the maximal accumulation degree among its nodes. Here your task is to find the accumulation degree of the given trees.

Input:

The first line of the input is an integer T which indicates the number of test cases. The first line of each test case is a positive integer n. Each of the following n - 1 lines contains three integers x, y, z separated by spaces, representing there is an edge between node x and node y, and the capacity of the edge is z. Nodes are numbered from 1 to n.
All the elements are nonnegative integers no more than 200000. You may assume that the test data are all tree metrics.

Output:

For each test case, output the result on a single line. 

Sample Input:

1
5
1 2 11
1 4 13
3 4 5
4 5 10

Sample Output:

26

题意：

给出一棵树，树上的边都有其权值，让我们求一个点能往外流的最大流量（会受到其它边权容量的限制）。

 

题解:

我们可以对于每个点进行一次树形dp来求，但是显然时间复杂度很高，会TLE...

我们考虑先对1号点dp一次，并且维护每个结点的dp值，表示当前结点流向其子树的最大流量，然后再dfs一次进行换根。

换根的过程中我们需要考虑清楚我们需要哪些知道量，需要更新哪些量，子节点的值能否被父亲结点更新。

这一题中，我们从u->v，假设已经知道了f(u)，即以u为根的最大流量（不同于之前的dp数组），那么对于v而言，f(v)=dp(v)+min( w(u,v) , min( f(u)-min(w(u,v),dp(v))  ) )。

要注意下u的另一颗子树即g[u].size()=1的情况，这时转移直接为f(v)=w(u,v)+dp(v)。

 

具体见代码吧：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <queue>
#define INF 1e9
#define mp make_pair
#define pii pair<int,int>
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int N = 2e5+5;
int n,T;
int dp[N];
vector <pair<int,int> > g[N];
void dfs(int node,int pa){
    int tmp = 0;
    for(int i=0;i<g[node].size();i++){
        int v=g[node][i].first,w=g[node][i].second;
        if(v==pa) continue ;
        dfs(v,node);
        tmp+=min(dp[v],w);
    }
    if(tmp>0) dp[node]=tmp;
    return ;
}
int ans=0;
void go(int u,int pa,int sum){
    ans=max(ans,sum);
    int len = g[u].size();
    for(int i=0;i<len;i++){
        int v=g[u][i].first,w=g[u][i].second;
        if(v==pa) continue ;
        if(len==1) go(v,u,dp[v]+w);
        else go(v,u,dp[v]+min(sum-min(dp[v],w),w));
    }
}
int main(){
    cin>>T;
    while(T--){
        scanf("%d",&n);
        if(n==0){
            puts("0");
            continue ;
        }
        ans=0;memset(dp,INF,sizeof(dp));
        for(int i=1;i<=n;i++) g[i].clear();
        for(int i=1;i<n;i++){
            int u,v,w;
            scanf("%d%d%d",&u,&v,&w);
            g[u].push_back(mp(v,w));
            g[v].push_back(mp(u,w));
        }
        dfs(1,-1);
        for(int i=1;i<=n;i++) dp[i]=(dp[i]==INF?0:dp[i]);
        go(1,-1,dp[1]);
        cout<<ans<<endl;
    }
    return 0;
}