路网匹配解决方案
路网匹配解决方案
建模过程
要素
- 路网由路段组成;
- 基站网络由各个基站位置组成;
- 基站序列
匹配过程
- 输入为基站网络中的基站序列
- 输出为路段序列
- 匹配过程为:寻找某一个路段为起点,最后寻找他周边的连通路段,逐渐在搜索空间中扩充路径,最终得到(一条或多条)完整路径,可以在此基础上再对路径进行调整改进与选择。
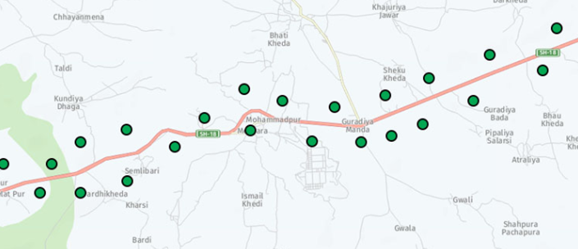
问题归纳
路网匹配与TSP旅行商问题、VRP车辆路径问题同属于NP难的组合优化问题,也是序列决策问题(任何组合优化问题都可以转化为一个多阶段的决策问题,即动态规划问题(但求解时会遭遇维度灾难))。
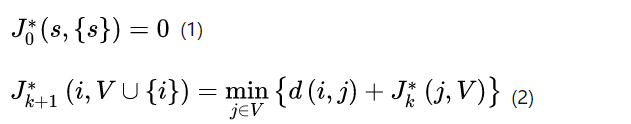
组合优化问题的解决思路
- 分支定界法(可以使用其他启发式方法来辅助进行分支节点的选取(类似在篱笆图中使用强化学习来进行辅助))
- 贪婪算法、局部搜索算法、松弛算法、动态规划法
- 启发式算法是一种基于直观或经验构造的算法,能在可接受的计算成本内尽可能地逼近最优解,得到一个相对优解,但无法预计所得解与最优解的近似程度
- 元启发式算法(进化算法) 是随机算法与局部搜索算法相结合的产物,包括禁忌搜索算法、模拟退火算法、遗传算法、蚁群算法、粒子群算法、人工神经网络(代指Hopfield能量网络)等。
- 序列生成模型,如RNN、seq2seq模型
- 序列决策模型,如强化学习
- 图模型,如图神经网络
++== 现在的趋势是使用多种方法结合求解! ==++
从动机角度理解机器学习在组合优化问题上的使用
在组合优化算法中使用机器学习的方法,主要有两方面:
-
优化算法中某些模块计算非常消耗时间和资源,可以利用机器学习得出一个近似的值,从而加快算法的速度。
动机(1)下使用的是 demonstration setting(模仿学习) 这种策略呢就是不断模仿expert做的决策进行学习,也没有什么reward啥的,反正你怎么做我也怎么做。他是通过一系列的“样例”进行学习,比如你把TSP问题的输入和最优解打包丢给他,让他进行学习,当他学有所成时,你随便输入一个TSP的数据,他马上(注意是非常快速的)就能给出一个结果。这个结果有可能是最优的,也有可能是近似最优的。在demonstration setting下,学习的目标是尽可能使得policy的action和expert相近。
当然,如果有了真实实例,那么也可以逼近真实解

1.1 在求解线性规划时,通过添加切割平面(cutting plane)可以拉紧(tighten)当前的松弛(relaxation),从而获得一个更好的下界(lower bound),暂且将加入cutting plane后lower bound相比原来提升的部分称之为improvement吧。Baltean-Lugojan et al. (2018) 使用了一个neural network去对求解过程中的improvement进行了一个近似。
1.2 使用分支界定法(branch and bound)求解混合整数规划问题(mixed integer programming)的时候,如何选择分支的节点,非常重要。一个有效的策略,能够大大减少分支树的size,从而节省大量的计算时间。目前表现比较好的一个启发式策略是strong branching (Applegate, Bixby, Chvátal, & Cook, 2007),该策略计算众多候选节点的linear relaxation,以获得一个potential lower bound improvement,最终选择improvement最大那个节点进行分支。尽管如此,分支的节点数目还是太大了。因此,Marcos Alvarez, Louveaux, and Wehenkel (2014, 2017)使用了一个经典的监督学习模型去近似strong branching的决策。He, Daume III, and Eisner (2014)学习了这样的一个策略--选择包含有最优解的分支节点进行分支,该算法是通过整个分支过程不断收集expert的behaviors来进行学习的。
1.3 当然强化学习与模仿学习可以结合,主要是使用模仿学习来初始化强化学习的策略。2019年Mila等机构的论文《Exact Combinatorial Optimization with Graph Convolutional Neural Networks》也是采用类似的思路,使用模仿学习来学习branch-and-bound算法中的变量选取策略,同时它还结合了图卷积神经网络。branch-and-bound求解过程需要不断地进行节点选取和变量选取,这可以看作是一个序列化决策问题。传统的方式是通过专家设计的启发来最小化求解时间。这是我们希望通过机器学习替代的部分。对于节点选取问题,strong branching是一种较为理想的启发,它可以产生很简单的搜索树,但缺点是计算量非常大,以至于不可能应用于所有节点。为了解决该决策过程的编码和难以泛化的问题,文中采用图卷积神经网络来建模,输入为二分图状态。图卷积神经网络有对输入规模伸缩性好,计算复杂度仅和密度相关(善于处理稀疏结构)和permutation-invariant的优点。模型的训练通过模仿学习和近似strong branching。该方法使得学习的策略有好的泛化能力,即在训练中学习到的策略可以用于更大规模的问题实例中。实验部分将之用set covering等四个NP-hard问题,说明在大规模问题中比SOTA solver中的专家设计启发有优势。
-
现存的一些优化方法效果并不是那么显著,希望通过学习的方法学习搜索最优策略过程中的一些经验,提高当前算法的效果。
动机(2)意在发现新的策略,policy是使用reinforcement learning通过experience进行学习的。他是通过一种action-reward的方式,训练policy,使得它不断向最优的方向改进。当然了,这里为了获得最大的reward,除了使用reinforcement learning algorithms的方法,也可以使用一些经典的optimization methods,比如genetic algorithms(遗传算法), direct/local search。
2.1 在TSP问题中,获得一个可行解是非常容易的一件事,我们只需要依次从未插入的节点中选择一个节点并将其插入到解中,当所有节点都插入到解中时,就可以得到一个可行解。在贪心算法中,每次选择一个距离上次插入节点最近的节点,当然我们最直接的做法也是这样的。但是这样的效果,并没有那么的好,特别是在大规模的问题中。所以就可以使用强化学习来改善贪心算法。具体可以参考下面这篇推文: Khalil, Dai, Zhang, Dilkina, and Song (2017a)构建了一个贪心的启发式框架,其中节点的选择用的是graph neural network,一种能通过message passing从而处理任意有限大小graphs的neural network。对于每个节点的选择,首先将问题的网络图,以及一些参数(指明哪些点以及被Visited了)输入到neural network中,然后获得每个节点的action value,使用reinforcement learning对这些action value进行学习,reward的使用的是当前解的一个路径长度。

强化学习与其他方法的结合
为什么要引入强化学习?
- 对于监督学习来说算法质量很大程度上取决于训练集的质量。为了克服监督学习的局限,于是强化学习被引入了进来。对于NP-Hard的组合优化问题,很多时候没有办法获取给定例子的最优解,因此需要使用RL这种更加高效的search方法来进行训练而非监督学习。
- 组合优化问题天然可以建模成一个序列决策过程
- 在很多组合优化问题中,强化学习的设定与问题比较配对。例如旅行商问题评价的指标是路径长度,直接拿这个做loss对网络而言是不可导的,而强化学习天然适合这种输出与loss没有直接关系的情形。因此目前的几十篇paper里面都是使用RL来让神经网络可以反向传播从而更新参数。
强化学习/近似动态规划就是针对传统动态规划的不足而来的。通过一些近似的方法来降低计算量,解决传统动态规划的问题。那么近似的思路有哪些?
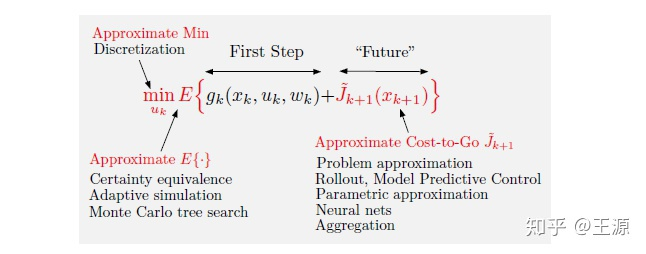
三种近似的思想:
- Approximate Min:简单来说就是 我们在求解极小化问题的时候可以不用那么较真,能求到一个差不多的近似最优解就可以了。也就是说拉紧下界bound时不用那么紧
- Approximate 期望:这个也比较好理解了,很多时候我们并不知道随机变量的分布,也就很难计算出期望的close form,那我们只好采用估计的方法来近似期望,例如采用样本均值来估计期望就是一种方式 (当然由于TSP问题没有随机变量在里边自然无需期望)。
- Approximate cost-to-go function(value function) :动态规划的关键就在这个上了,要想精确得到这个,需要再求解一个子优化问题,然后像剥洋葱一样层层递推到最后才能算出来,那么我可以通过近似未来的cost的方式来降低计算量,我只计算一个近似的cost-to-go function 。那么我们这一过程称为Approximation in value space (值空间近似)。
从求解思路上来说这些paper的对组合优化的马尔可夫建模思路也可以再分成两类:
- 一类是基于局部解让网络输出新加入的节点来拓展当前的局部解,迭代若干次从而得到完整解;
- 另一类是基于一个完整的解让网络输出对当前解的改进操作,从而提高解的质量,当达到迭代阈值时选取整个过程中最好的解作为最后的结果
- 强化学习与分支定界法结合:分支定界算法的效率取决于从哪个变量 branch 和 node selection两个因素,如果branch 和 node selection的策略比较好,那么分支定界算法可以很快的剪枝或者可以很快的得到比较好的界,就可以大大提升分支定界算法的效率。目前对于 branch 和 node selection的策略还没有公认的太好的方法。传统的方法基本上都是一些简单的启发式规则,那么强化学习可以帮助我们有效的给出一个 branch 和 node selection的策略。这样的一种策略也被称为Learning to search,有别于以往单纯的基于Search的传统优化方法,Learning to search还是在优化过程中引入学习的概念帮助更加有效的搜索最优解。2014年在NIPS会议上,文章Lodi A, Zarpellon G. On learning and branching: a survey[J]. TOP, 2017: 1-30.是比较早的一个用机器学习算法来学习分支定界算法里边的 branch 和 node selection的策略的
目前的paper使用强化学习解决组合优化时他们的contribution或者说novelty主要是集中在对网络结构的设计上,即如何设计一个能handle住组合优化对应的数据结构的network architecture。
-
序列模型:把问题建模成一个sequence形式的input,然后想办法使用基于attention的魔改结构(可以是比较裸的self-attention,也可以是进一步的把transformer搬过来)来提取feature给结果。
序列模型有专为组合优化求解而诞生的神经网络Pointer Network(Ptr-Net)。是基于Sequence-to-Sequence网络生成的一种新的网络架构。Ptr-Net与Sequence-to-Sequence类似,都是解决从一个序列到另一个序列的映射问题,不同的是Ptr-Net针对的序列问题更加特殊:输出序列的内容与输入序列的内容完全一致,只是序列的顺序发生了改变。这种问题在实际中常见的应用就是组合优化问题,因此Ptr-Net首次建立了神经网络与组合优化问题的联系。Ptr-Net正是利用了注意力机制解决了对输入序列排序的问题。通过注意力机制,可以计算出当前输出与输入序列关系最大的元素,那么我们就将输入序列的元素作为该输出元素,每一个输出元素都像有一个指针一样指向输入元素,Pointer Network因此得名。需要注意的是,每个输入元素只能被一个输出元素所指,这样就避免了输入元素的重复出现,下图给出Ptr-Net的基本结构图:
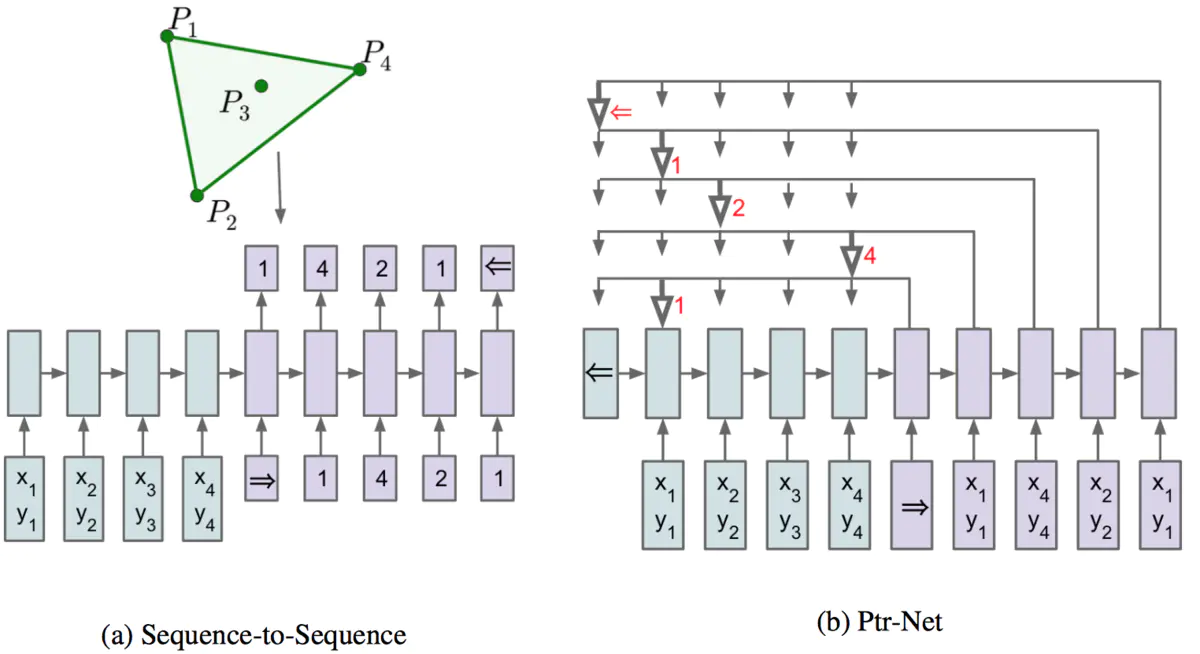
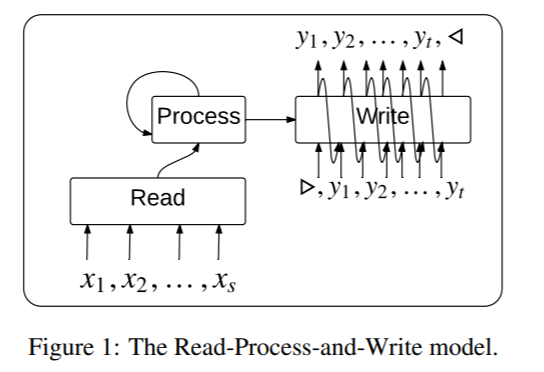
对于无序输入数据,2015年Google的论文《Order Matters: Sequence to sequence for sets》提出了Read-Process-and-Write架构。它由三个网络组成。开始的Read部分是一个神经网络将输入进行嵌入得到对应的memory vector;接下来,Process部分是一个没有输入或输出的LSTM,它用前面的memory vector通过注意力机制进行一定步数的计算,得到相对于输入permutation invariant的隐状态;最后,Writer部分是一个LSTM Pointer Network,它的输入为Process部分输出的隐状态,以及Read部分输出的memory vector,产生最终的输出。这里相对于原始的Pointer Network,在pointer部分前加了一个额外的注意力机制(因为原来的注意力机制被用来输出结果了),称为glimpse机制。对于无序输出数据,文中提出一种高效的训练算法,它在训练和推理时搜索所有可能的顺序。对于像TSP和triangulation等问题,其解中存在大量的等价类。对于这些等价类做一些约束,有利于更快地收敛。如对于TSP,可以从输入的第一个元素开始,然后按逆时针顺序输出,准确率能有所提高。
-
序列模型结合强化学习:序列模型作为策略参数来通过强化学习进行进一步调整。 2016年Google的的论文《Neural Combinatorial Optimization with Reinforcement Learning》提出了Neural Combinatorial Optimization(NCO)。在神经网络模型方面,它使用前面提到的Ptr-Net架构作为策略模型,然后使用基于梯度的强化学习方法(REINFORCE算法)来学习策略模型的参数。它将每个问题实例作为一个训练样本。对于TSP问题来说,训练的目标函数是给定一个图的期望旅途长度。基于梯度的强化学习用于减少方差的一个常用方法是引入一个baseline function。文中引入了另一个RNN网络作为这个baseline function,它估计给定输入序列下的的期望旅途长度。该网络以均方误差MSE为目标函数并使用随机梯度下降SGD来优化。另外,文中指出结合推理时搜索还能进一步改善效果。由于评估一条旅途的长度只需很小计算量,因此可以让模型输出很多候选,然后在里边找最优的。这样就可以衍生出Sampling和Active Search两种策略。前者通过采样得到大量候选解,然后找到其中的最优解。后者针对给定的问题实例,在推理时对策略模型参数进行refine,以最小化该问题实例下的期望旅途长度。这两种策略还可以与强化学习的预训练模型结合。实验部分该方法被应用于TSP和KNAPSACK问题。TSP问题考虑的规模为20, 50和100个城市。结合推理时优化,TSP的解可以胜于Christofides algorithm以及OR Tools(通过local search与LK heuristic提升Christofides’ solution)。(感觉最新的方法可能针对的TSP规模都不是很大,在更大规模上可能没有启发式的好,启发式的baseline本身就很高了)
-
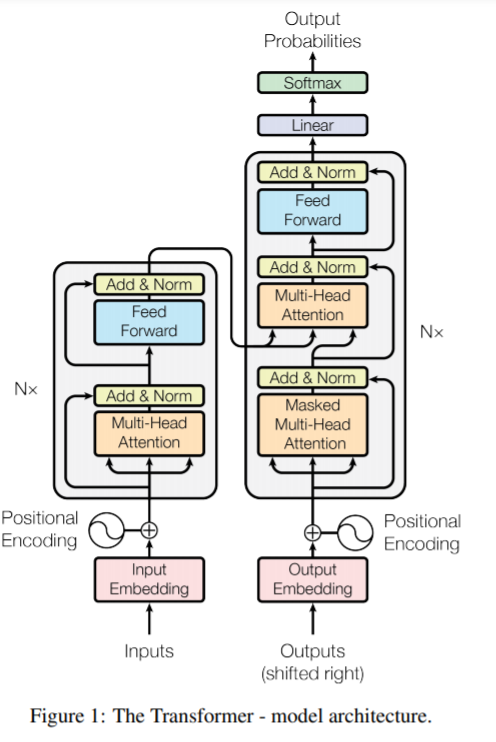
Transformer模型: 2017年Google的论文《Attention Is All You Need》仅仅使用了注意力机制,没有使用于RNN,LSTM或者CNN对序列建模。Transformer延续了encoder-decoder架构,其encoder和decoder网络均由层叠的self-attention和point-wise fully connected层组成(原论文图1)。这里的注意力机制和以前Seq2Seq模型中的注意力机制有所不同,这是称为Multi-Head Attention(MHA)的Self-Attention机制(原论文图2),该模型除了准确率更高,还更易并行,且训练也更快。

-
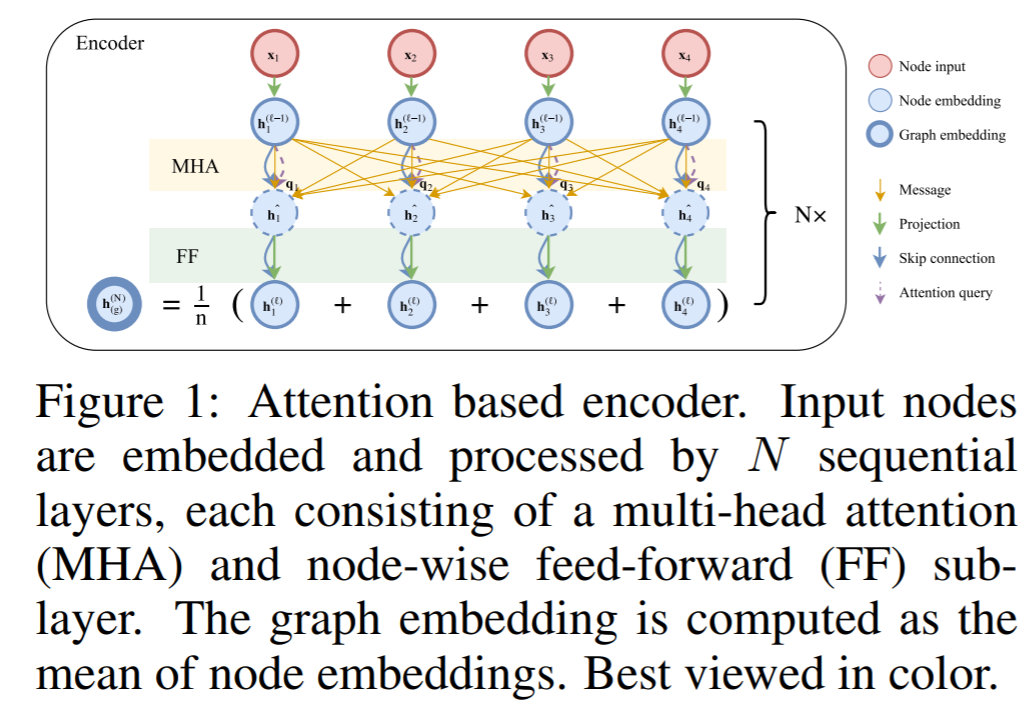
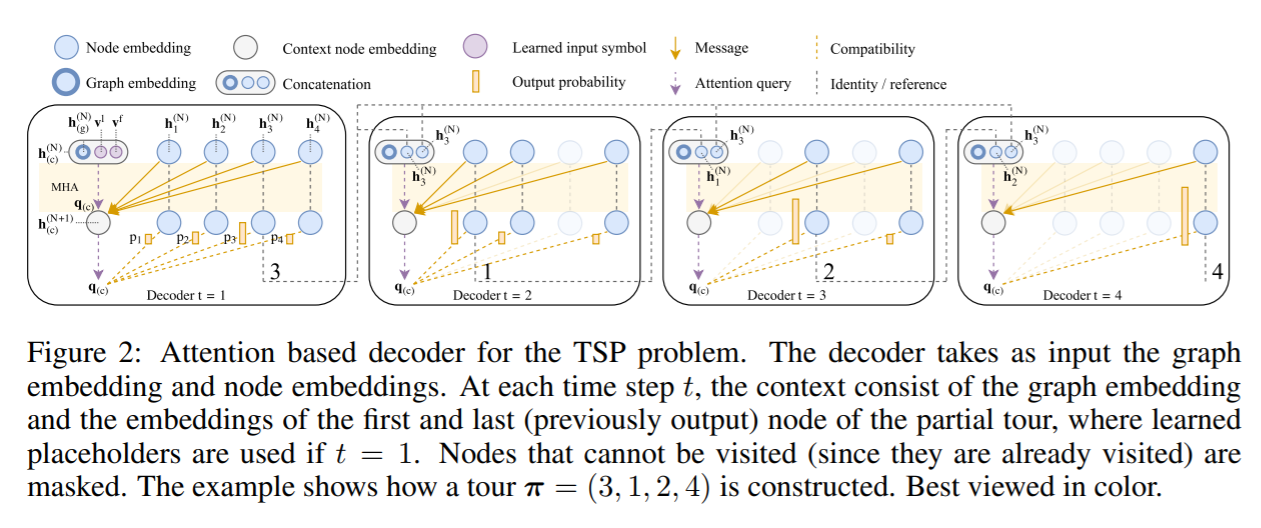
Transformer模型与强化学习结合:2018年巴黎综合理工学院等机构的论文《Learning Heuristics for the TSP by Policy Gradient》基于前面NCO的主要思想,与原Transformer模型相比,encoder部分中没有用positional encoding,这样便使node embedding与输入顺序无关。其它部分基本沿用了Transformer架构中层叠的multi-head attention(MHA)和feed-forward(FF)结构来得到每个城市对应的node embedding。node embedding的平均作为graph embedding。这个embedding会输出给decoder。Decoder采用了经典的autoregressive模式,在每一步中,基于encoder的embedding和之前步的输出,得到当前步的输出。Decoder网络基于注意力机制,与前面工作一大区别在于它引入了context node来表征解码时的上下文,它包含了graph embedding,以及第一个节点(它是起点也是终点)与前一个输出节点的embedding。这个context node加上其它的embedding信息通过MHA层(与encoder中的MHA相比,这里为了高效没有skip-connection, BN和FF子层)得到输出向量。最后,decoder结构有一个single attention head(即M=1的MHA),通过softmax输出即为当前步的输出。训练使用的仍是经典的REINFORCE算法,这里有些区别的是baseline function是通过rollout的方法得到的,即基于当前最好的策略模型进行deterministic greedy rollout得到。实验部分主要考虑了多种路径问题,如TSP和VRP的多种变体(如SDVRP, PCTSP, SPCTSP)。在很多case中,与构造类heuristic(Nearest, Random and Farthest Insertion和Nearest Neighbor),OR Tools,Christofides+2-OPT local search以及其它基于机器学习的方法相比能得到更优的解。
-
图模型:把问题建模成一个graph形式的input,然后想办法基于GNN和基于GNN的attention的魔改结构来提取feature给结果。主要包括图嵌入模型作为表示学习与图神经网络解决图任务两部分,其中互有重叠,GE与GNN是两个维度的概念,前者指一种任务,后者指完成很多任务的一类模型。但由于它们之间关系紧密,所以放在一起讨论。
-
一个相对早些的将GE引入的工作是2017年佐治亚理工学院的论文《Learning Combinatorial Optimization Algorithms over Graphs》,它也成为了后面很多新方法的对标对象。对于组合优化问题,一个困境是对于同样类型,但数据不同的问题,我们常常需要一遍遍地重新去解决。因此文中比较正式的提出了灵魂拷问:给定一个图优化问题和一个问题实例的分布,有没有办法可以让heuristic泛化到那些不曾见过的问题实例。它还指出之前很多基于机器学习的组合优化算法都是通用的,因此没有充分挖掘图这种特殊的结构。为了解决,它将GE与RL进行了结合,提出了S2V-DQN算法。这里的GE用的是他们在2016年论文《Discriminative embeddings of latent variable models for structured data》中的structure2vec(S2V)方法。强化学习部分考虑前面工作普遍采用的policy gradient样本效率不高,因而使用了Q-learning。该方法基于贪心算法框架,每一步中,基于当前的部分解,选取使评估函数最大的节点。可以看到,这里评估函数非常重要,它需要能够提取和表达图中的各种信息。为了做到这一点,structure2vec被用来做图嵌入以及参数化评估函数。为了优化评估函数中的参数,该评估函数可以作为Q-learning中的Q函数,然后进行训练。与前面的模型相比,该模型中没有使用单独的encoder和decoder,而是一个基于GE的单个模型。实验部分在Minimum Vertex Cover,Maximum Cut和TSP上与NCO,以及每种问题相关的heuristic方法进行了对比,并在optimality gap指标上得到了更优的解(尤其是对于像MVC这种图结构信息更重要的问题)。对于MVC和TSP规模分别达到500和300左右。另外GE使得训练好的模型应用到更大的图上。实现中拿在50-100节点的问题上训练的模型应用到更大规模的问题(最大到1200)取得了很小的approximation ratio。
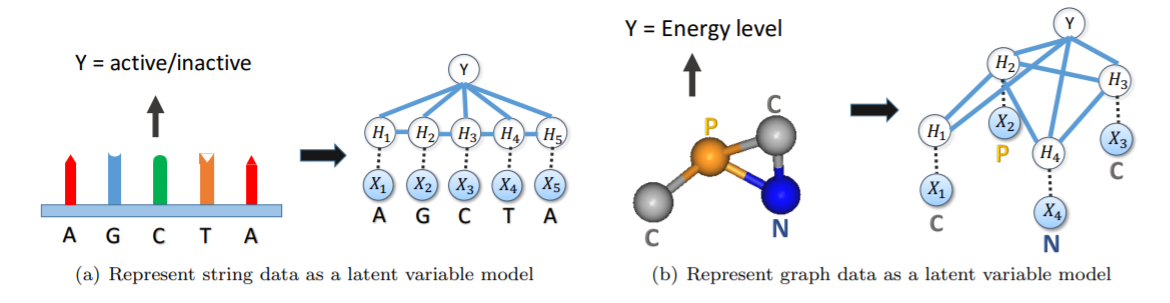
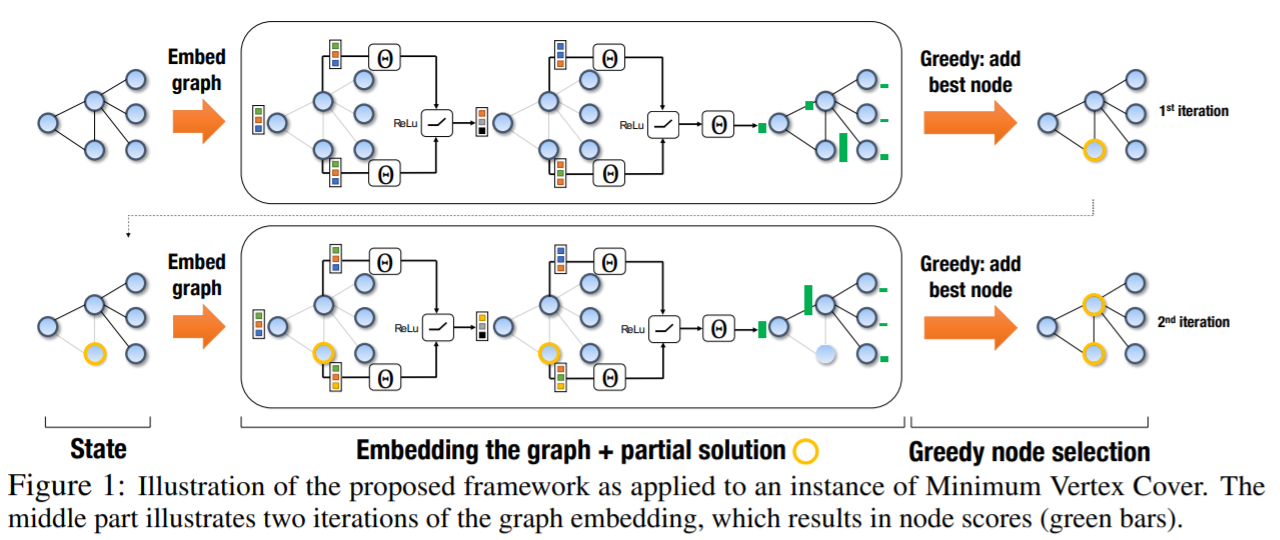
(在解决方案构建过程的每次迭代中,神经网络会观察当前的图表,并选择一个节点添加到解决方案中,然后根据该选择更新图表,接着重复这个过程,直到得到一个完整的解决方案。使用DQN算法来训练神经网络。缺陷就是他们会使用一个“辅助”方程来帮助图神经网络寻找更好解法。这个辅助方程是人为设计用于解决特定问题的)GNN中重要的一种就是结合了卷积的图卷积网络(Graph Convolutional Network,GCN)。它在很多解关于图的组合优化的工作中都有用到。2019年德里印度理工学院与加州大学圣巴巴拉分校的论文《Learning Heuristics over Large Graphs via Deep Reinforcement Learning》提出一种称为GCOMB的深度强化学习框架用于学习大规模图下的组合优化问题。与前面的文章目的类似,它的目的也是让算法能解决来自与训练集中同分布的但未见的问题实例,但它将之扩展到更大规模的问题(百万级节点)。整个算法包含训练与推理两个阶段。训练阶段又分两个子阶段:第一步用GCN作为embedding,通过监督学习的方式学习GCN中的参数。它本质上是让embedding能反映每个节点对于解的重要程度;第二步基于Q-learning用于形成解集。将回报设定为加入某节点后的边际收益,然后进行训练。在推理阶段,对于给定的图,先用训练好的GCN进行embedding,然后通过Q-learning学习的Q函数迭代地计算解。即用贪心算法以增量方式构造解。
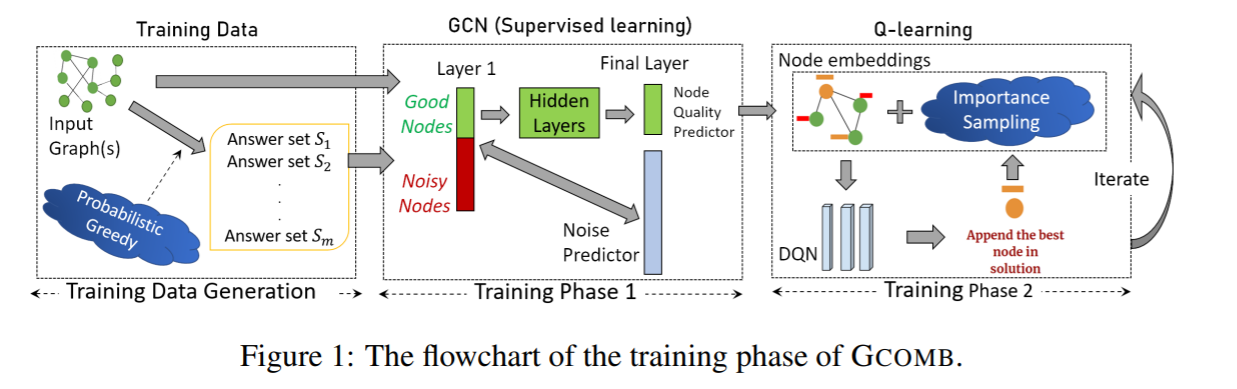
2017年纽约大学的论文《A Note on Learning Algorithms for Quadratic Assignment with Graph Neural Networks》引入了GNN来解决二次分配问题(Quadratic assignment problem,QAP)这个NP-hard问题。TSP可看作是QAP的一种特例因此也被提及。该文以监督学习的方式训练GNN,并直接以邻接矩阵的形式输出解,然后通过beam search找到可行解。相比前面挨个输出解中元素,也就是autoregressive的方式,这种是一下子输出解的方式称为non-autoregressive的方法。但在TSP上似乎效果不如Ptr-Net和Christofides算法,原因可能是由于监督学习下解的质量依赖于ground truth,而ground truth又来自于heuristic(LK Heuristic)。2019年南洋理工大学和洛约拉马利蒙特大学的论文《An Efficient Graph Convolutional Network Technique for the Travelling Salesman Problem》基于《Residual Gated Graph Convnets》中的Graph ConvNets和beam search算法来解决TSP。对于50和100个节点的TSP它将optimality gap缩减到0.01%和1.39%,超越了当时其它基于深度学习的方法。首先,该模型以TSP的图为输入,通过Graph ConvNet进行表征学习,然后edge embedding经过MLP得到概率矩阵。如果将TSP解中旅途表示成邻接矩阵的话,那该输出的概率矩阵就可以看作邻接矩阵的heat map。这种以non-autoregressive的方式输出邻接矩阵与上一篇论文中是类似的。然后,该模型使用监督学习进行训练,训练集中的解通过Concorde求解器得到。在推理时,基于模型得到的邻接矩阵可以通过beam search算法转为合法的旅途,即TSP的解。对于Graph ConvNet和beam search,都可以被并行化通过GPU加速,因此在性能上可以有一定优势。同时,文中也指出与autoregressive模型相比,该模型的泛化能力较差。另外,因为是基于监督学习,意味着它处理的问题规模会有瓶颈。

2018年剑桥大学等机构的论文《Graph Attention Networks》提出Graph attention networks(GAT)。它将注意力机制的思想引入到GNN,即可以让节点将注意力放到某些邻接节点上。它成为了近几年中图相关问题网络模型主流方法之一。2020年康奈尔大学和哥伦比亚大学的论文《Learning to Solve Combinatorial Optimization Problems on Real-World Graphs in Linear Time》就是应用了GAT,并提出一种针对图结构组合优化问题的框架。它在一个训练集上使用强化学习训练GNN,训练好的神经网络可以对于一个新的图实例输出近似解。该框架比较有特色的是引入了edge-to-vertex line graph(原图中的每条边对应这个图中的节点)用于那些需要选取边的问题(如MST)。GNN用来学习图的表征并输出选取节点的策略。这个GNN基于经典的encoder-decoder架构。Encoder部分基于GAT,decoder使用了注意力机制。整个网络的计算保持在线性复杂度。该方法通过不同的目标函数可以适用于多种基于图的组合优化问题。它在解的质量(optimality gap接近于1)与运行性能(线性执行时间)上都有好的表现。
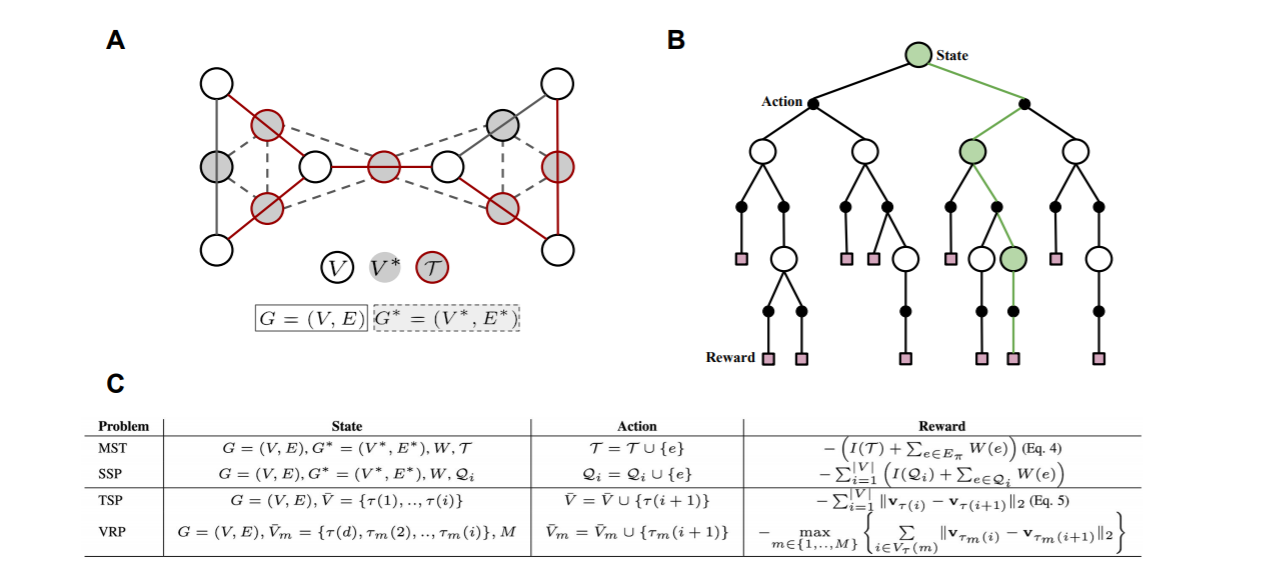
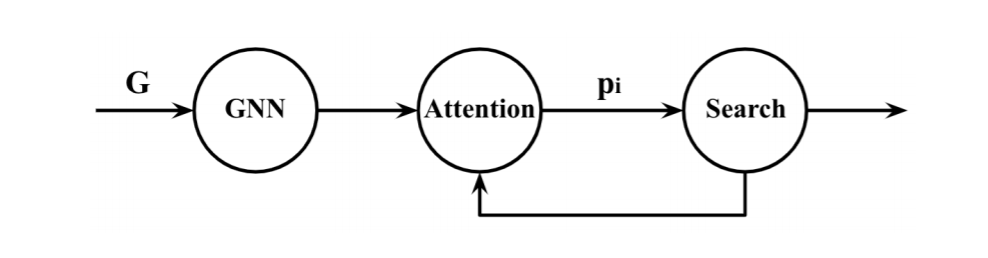
当然我认为与序列+图并不矛盾,但是主体只能有一个
RL反而变成了一个固定工具,有DQN(基于值函数的)和PG(基于策略的)(应该还有actor-critic),而且基本都是最原始的加上去并且基本没有对RL算法有什么额外修改。
最近两年的相关的AI顶会paper告诉我们:Attention mechanism可以处理组合优化对应的数据结构,RL loss可以用于网络的训练
参考
https://www.zhihu.com/question/406601430
https://blog.csdn.net/weixin_39970064/article/details/111528715
后处理
前面的介绍可以看到,基于深度学习的方法已经在组合优化问题中达到还不错的成绩。另一方面,我们也可以看到,这些方法大多数还是需要结合一些后处理的。比如不少工作中对于机器学习模型表示概率的输出,需要经过一些后处理算法得到最终的解。
如常用的包括:
- Greedy:每次选取输出概率最高的节点。
- Beam search:本质上是宽度受限的广度优先搜索。
- Sampling:采样一定数量的解,取最优。
- 还有些工作是结合了像2-OPT算法来进一步提高解的质量。
与前面几种方法不同,像2-OPT,3-OPT这种是对一个完整的解进行局部修改来试图改进它,称为perturbative search(扰动搜索)。那么问题来了,这些搜索过程在整个算法中的影响如何?我们又如何评估机器学习部分的算法能力呢?2019年蒙特利尔综合理工学院等机构的论文《How to Evaluate Machine Learning Approaches for Combinatorial Optimization: Application to the Travelling Salesman Problem》就是主要针对该问题。它指出常用的评估指标optimality gap同时针对机器学习和搜索部分,因而无法准确评估机器学习部分算法。为此它提出了一种新的测度,称为ratio of optimal decision(ROD)。其优点是可以排除搜索部分带来的影响,只评估机器学习部分的效果。它的主要思想是将问题看作序列化问题,并关注每一步决策的质量。这样那些大多数步里做了最优的决策,但因一步之差导致optimality gap不理想的情况就不至于得分很低。另外,通过实验它还说明了搜索过程对于机器学习方法的影响巨大。一些基于机器学习的方法得到的解在经过如2-OPT,3-OPT和LK等方法refine后其optimality gap能够显著降低。
以往的很多工作中基本是以增量的方式构造解,每当一步决策后,它们通常不会再重新考虑之前所做的决定。而2019年牛津大学等机构的论文《Exploratory Combinatorial Optimization with Reinforcement Learning》则是在推理时进行探索以获取更优的解。本文提出exploratory combinatorial optimization(ECO-DQN)方法,适用于定义于图结构上的组合问题。概括来说,ECO-DQN可以归结为S2V-DQN+RevAct + ObsTun+IntRew。其中的S2V-DQN指前面《Learning Combinatorial Optimization Algorithms over Graphs》提出的方法。RevAct(Reversible Actions)指允许flip一个节点多次。ObsTun(Observation Tuning)指状态包含7个观察,分别基于vertex state等。它们提供了多方面的信息,用于确定选取动作的价值,提供历史信息避免过短环路,保证外部和内部回报符合马尔可夫特性,以及有限步的episode。IntRew(Intermediate Rewards)指通过reward reshaping,当达到新的局部最优解时,给一个小的中间回报,作为内部回报。这样主要为了克服回报稀疏的问题。在Maximum Cut Problem上,它的表现性于SOTA的强化学习方法。另外,该算法可以从任意的解开始。因此,可以与其它的搜索方法结合进一步提升。
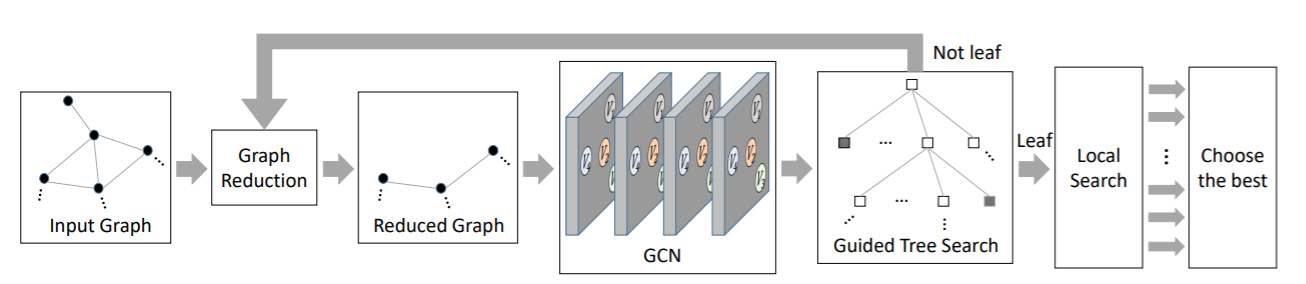
2018年Intel Labs和香港科技大学的论文《Combinatorial Optimization with Graph Convolutional Networks and Guided Tree Search》结合了图卷积网络与树搜索来解决组合优化问题。它主要思想是基于图卷积网络输出节点属于最优解的概率,然后用它引导树搜索。这个图卷积神经网络模型通过监督学习来训练,因此它需要大量预先解好的问题实例。算法的流程分几步:首先,输入的图经过一个预处理,即graph reduction进行简化,然后喂给图卷积神经网络,输出多个概率图表示每个节点属于最优解的似然。至于为什么是多张概率图是有讲究的,文中提到最优解可能有多个,而一个节点可能出现在多个最优解当中,换言之,该概率分布是多峰的。另一方面,这样做可以生成很多候选解,有利于后面树搜索中更好的探索。接下来,这些概率图就用来在树搜索中以迭代的方式构造解。最后还会用local search(2-improvement local search算法)看看能不能改善解。实验中基于MIS,MVC,MC,SAT等多个NP-hard问题与S2V-DQN,Z3,ReduMIS,Gurobi等方法做了比较,在数据上优于这些方法,且对于问题类型和数据集的泛化能力强。另外,树搜索是容易并行加速的,因为可以将部分解的扩展放到多个线程运行。
2019年UC Berkeley和Facebook的论文《Learning to Perform Local Rewriting for Combinatorial Optimization》提出了一种结合机器学习的基于搜索的方法。对于组合优化问题,传统的搜索通常依赖于启发,而在不同的场景中调优这个启发往往非常耗时。本文提出NeuRewriter方法来学习策略来重写当前解的局部组件,并以迭代的方式不断改进解直到收敛,优化问题被看作是重写问题,策略分为两部分组件:即region-picking策略和rule-picking策略。前者用于根据当前状态(每个解就是一个状态)选取要改的区域;后者选取重写的规则。这些网络模型通过神经网络来表示并用强化学习中的AC方法来训练。之前一些基于机器学习的方法很多是逐个节点添加构造解(即auto-regressive),而该方法是从一个可行解出发改进它找到更优解。实验中,NeuRewirter方法在expression simplification上超越了Z3,online job scheduling上超越了DeepRM与OR tools,CVRP上分别超越了一些基于机器学习的方法以及OR tools。

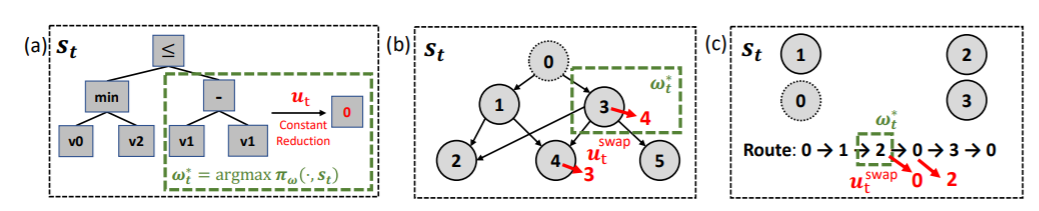
组合优化问题学习框架

路网匹配的方法
隐马尔可夫模型
隐马尔可夫模型建模为隐藏状态序列与观测状态序列。在路网匹配这个问题上,是从观测序列到隐藏序列进行逆采样的过程,忽略了状态节点之间的路径,一般假设为最短路径,
一般结合候选选择、篱笆图与维特比算法一套组合拳进行预测。篱笆图的节点与边分为设有权重。现有的工作一般是针对这些权重考虑的。比较特殊的是IVMM从构建了多个篱笆图来加权投票
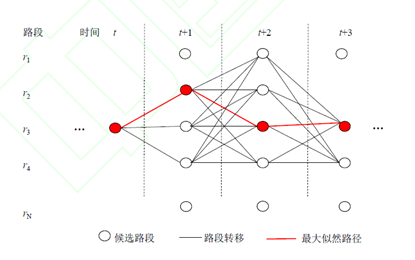
篱笆图是否必要?
使用篱笆图的好处:
- 将搜索空间压缩为有限空间,
- 可以将路网匹配转换为搜索树的问题,进而使用各种搜索方法解决。
使用篱笆图的不足:
- 使用篱笆图是对问题的一个简化,忽视了节点之间的路径选择,有助于减少搜索空间,但这里可能出现匹配不正常的部分。
- 使用篱笆图就需要候选选择,同样可以进一步减少搜索空间,由于采用误差进一步增大,也不是很可靠。
深度学习模型
针对基站的路网匹配主要是DMM与DeepMM
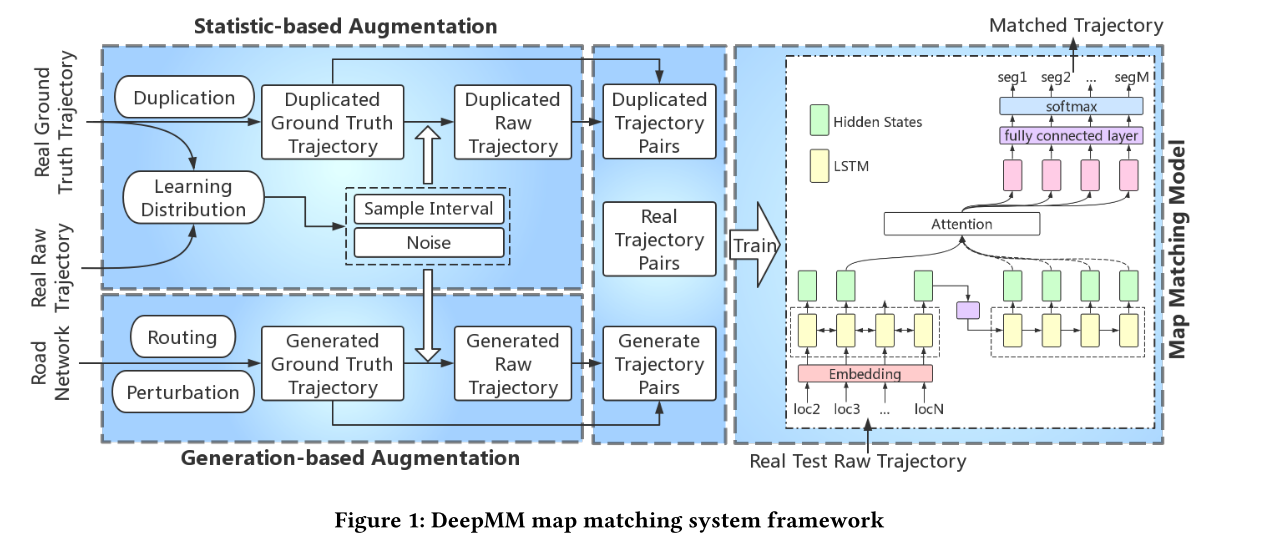
- DeepMM主要是数据增强(训练数据扩充)与序列模型解决路网匹配
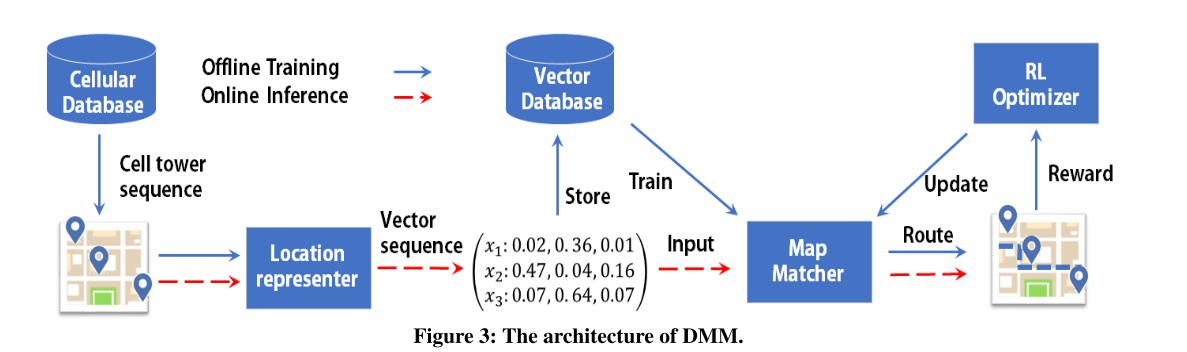
- DMM主要是简单的基站嵌入表示,以序列模型为策略参数的强化学习
未来可能的方法思路
==
第一部分,保留篱笆图,即简化中间路段选择部分
- 保留篱笆图,使用更强的图嵌入+强化学习+图搜索(强化学习+分支界定法)的方法解决
- 保留篱笆图,将篱笆图建模为序列模型,然后使用pointer-Net生成输出,通过强化学习policy训练pointer-Net参数
- 保留篱笆图,将篱笆图建模为拓扑图,然后输入到图神经网络每次输出一个节点,并依据输出节点更新图神经网络,直到全部输出。通过强化学习Q-learning训练
- 保留篱笆图,将篱笆图建模为拓扑图,将基站序列建模为子图,拓扑图中与基站序列相似的子图
第二部分,输出连续的所有路段组成路径,进一步分为一个一个路段生成(只能参考之前生成出来的部分),还是一次性全部生成(可以互相调整)。
- 使用序列模型建模,不只使用DMM的Seq2seq,而使用Transformer来做策略,进一步在强化学习部分使用A3C(值函数+策略)而不是只有policy结构
- 模仿学习,来使隐马尔可夫模型以线性时间预测
- 图结构建模+Attention机制(或者Transformer)可以实现对结果的输出(GCN作为Encoder,Attention作为Decoder),强化学习来进行参数调整训练
- 贪心框架下用图结构GCN建模+Q-learning的值函数贪婪地选择节点
- 训练GNN,并直接以邻接矩阵的形式输出解,然后通过beam search找到可行解(一下子输出解的方式称为non-autoregressive的方法)
第三部分,后处理对(多条)输出路径进行选择与调整(选择调整区域与更新收敛)
- 在上面提到的搜索方法中,使用Beam Search来保留多个解,更有机会逼近更优解。
- region-picking策略和rule-picking策略。前者用于根据当前状态(每个解就是一个状态)选取要改的区域;后者选取重写的规则。通过神经网络来表示并用强化学习中的AC方法来训练。
==


