算法技巧_二叉树
算法技巧(二叉树)
两种解题思路
- 遍历一遍树是否可以解决问题 如果可以，用一个 traverse 函数配合外部变量来实现。
- 分解问题 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值。
一旦你发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了
- 无论使用哪一种思维模式，你都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做
最简单的遍历二叉树代码
List<Integer> res = new LinkedList<>();
public void traverse(TreeNode root){
if(root == null){
return;
}
//前序位置
res.add(root.val)
traverse(root.left)
traverse(root.right)
//后序位置
}
遍历二叉树的方式
- 前序 （根左右）
- 中序 （左根右）
- 后序 （左右根）
- BFS （广度遍历搜索）
- DFS (深度遍历搜索)
前中后序遍历的区别以及各自场景
- 前序是自顶向下遍历的，后序是自底向上遍历的。前序位置的代码只能从函数参数中获取父节点传递来的数据
- 前序是刚刚进入节点的时刻，后序位置是即将离开节点的时刻。
- 后序位置代码不仅仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据
技巧
- 回溯
- 属于遍历的思路，它的关注点在节点间的「树枝」
- 它的着眼点永远是在节点之间移动的过程，类比到二叉树上就是「树枝」。
- 动态规划
- 动态规划算法属于分解问题的思路，它的关注点在整棵「子树」
- 它的着眼点永远是结构相同的整个子问题，类比到二叉树上就是「子树」
- DFS
- 属于遍历的思路，它的关注点在单个「节点」
- 它的着眼点永远是在单一的节点上，类比到二叉树上就是处理每个「节点」
典型问题
- 如果把根节点看做第一层，如何打印出第一个节点所在的层数？(遍历一遍树 前序位置打印层级)
- 如何打印出每个节点的左右子树各有多少节点？（分解问题 求出每个子树的节点 后序位置打印）
常见题目以及解题思路
- leetcode 二叉树的直径 求二叉树最长的直径
- 解题思路：
- 二叉树的长直径长度就是任意两个结点之间的路径长度 最长直径并不一定要求穿过根节点
- 关键：每一条二叉树的直径长度 就是一个节点的左右子树的最大深度之和。
class Solution { // 记录最大直径的长度 int maxDiameter = 0; public int diameterOfBinaryTree(TreeNode root) { maxDepth(root); return maxDiameter; } int maxDepth(TreeNode root) { if (root == null) { return 0; } int leftMax = maxDepth(root.left); int rightMax = maxDepth(root.right); // 后序位置，顺便计算最大直径 int myDiameter = leftMax + rightMax; maxDiameter = Math.max(maxDiameter, myDiameter); return 1 + Math.max(leftMax, rightMax); } }
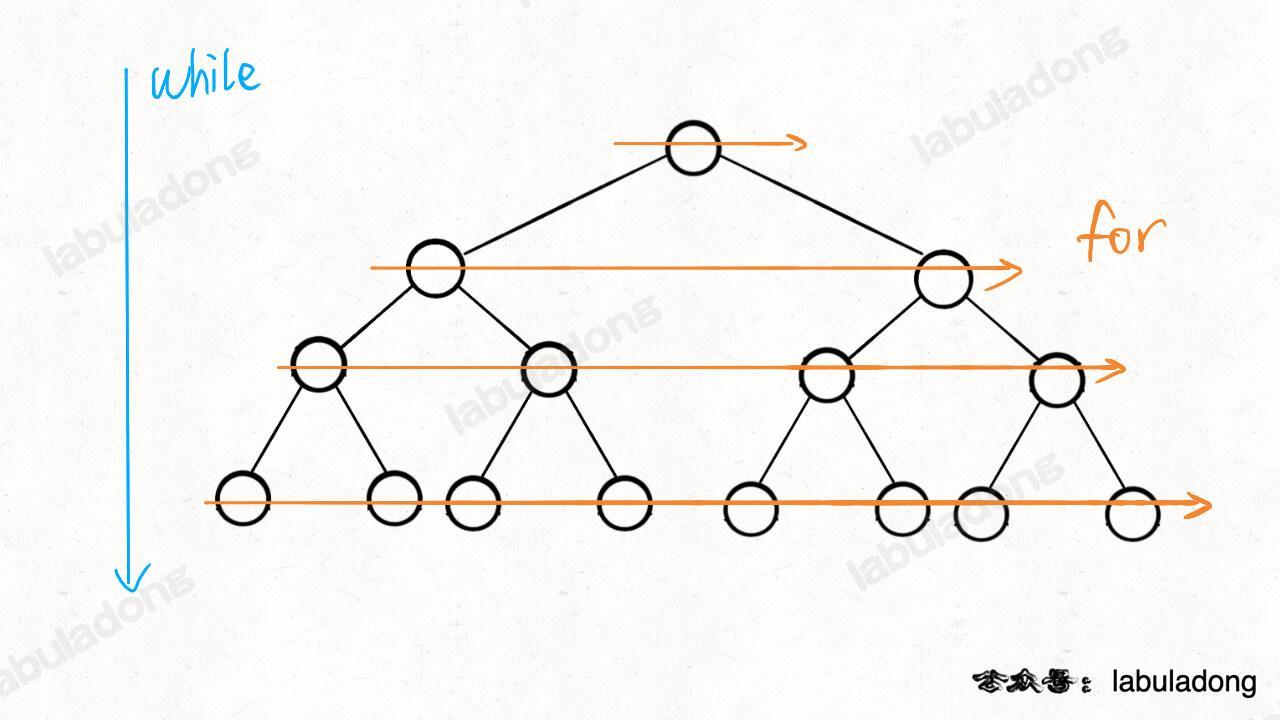
- BFS 实现
- 遍历实现
// 输入一棵二叉树的根节点，层序遍历这棵二叉树
void levelTraverse(TreeNode root) {
if (root == null) return;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
// 从上到下遍历二叉树的每一层
while (!q.isEmpty()) {
int sz = q.size();
// 从左到右遍历每一层的每个节点
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
// 将下一层节点放入队列
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}
}
- 递归解法
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<List<Integer>> levelTraverse(TreeNode root) {
if (root == null) {
return res;
}
// root 视为第 0 层
traverse(root, 0);
return res;
}
void traverse(TreeNode root, int depth) {
if (root == null) {
return;
}
// 前序位置，看看是否已经存储 depth 层的节点了
if (res.size() <= depth) {
// 第一次进入 depth 层
res.add(new LinkedList<>());
}
// 前序位置，在 depth 层添加 root 节点的值
res.get(depth).add(root.val);
traverse(root.left, depth + 1);
traverse(root.right, depth + 1);
}
}
