随笔 - B树算法实现
写代码之前,再回顾一下B树是什么,满足什么样的规则
B树规则:
- 排序方式:所有节点关键字是按递增次序排列,并遵循左小右大原则
- 子节点数:非叶节点的子节点数>1,且<=M ,且M>=2,空树除外(注:M阶代表一个树节点最多有多少个查找路径,M=M路,当M=2则是2叉树,M=3则是3叉)
- 关键字数:枝节点的关键字数量大于等于ceil(m/2)-1个且小于等于M-1个(注:ceil()是个朝正无穷方向取整的函数 如ceil(1.1)结果为2)
- 所有叶子节点均在同一层、叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针只不过其指针地址都为null对应下图最后一层节点的空格子
用一张图来帮助理解B树(为了方便理解,使用实际字母大小来排列)
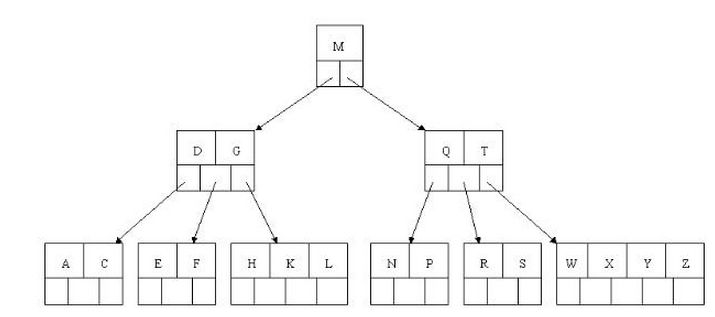
B树查询流程
如上图我要从上图中找到E字母,查找流程如下
- 获取根节点的关键字进行比较,当前根节点关键字为M,E<M(26个字母顺序),所以往找到指向左边的子节点(二分法规则,左小右大,左边放小于当前节点值的子节点、右边放大于当前节点值的子节点)
- 拿到关键字D和G,D<E<G 所以直接找到D和G中间的节点
- 拿到E和F,因为E=E 所以直接返回关键字和指针信息(如果树结构里面没有包含所要查找的节点则返回null)
B树节点插入规则
拿一个5阶树举例
- 节点拆分规则:当前是要组成一个5路查找树,那么此时m=5,关键字数必须<=5-1(这里关键字数>4就要进行节点拆分)
- 排序规则:满足节点本身比左边节点大,比右边节点小的排序规则
B树节点删除规则
- 节点合并规则:当前是要组成一个5路查找树,那么此时m=5,关键字数必须大于等于ceil(5/2)(这里关键字数<2就要进行节点合并)
- 满足节点本身比左边节点大,比右边节点小的排序规则
- 关键字数小于二时先从子节点取,子节点没有符合条件时就向向父节点取,取中间值往父节点放
B树特点
B树相对于平衡二叉树的不同是,每个节点包含的关键字增多了,特别是在B树应用到数据库中的时候,数据库充分利用了磁盘块的原理(磁盘数据存储是采用块的形式存储的,每个块的大小为4K,每次IO进行数据读取时,同一个磁盘块的数据可以一次性读取出来)把节点大小限制和充分使用在磁盘快大小范围;把树的节点关键字增多后树的层级比原来的二叉树少了,减少数据查找的次数和复杂度
讲了许多,对于程序猿来说,还是上代码实际
首先定义一个BTree,内部定义一个节点类
public class BTree<K, V> where K : IComparable<K>
{
private class Node
{
public Node Parent { get; set; }
public List<K> Keys { get; set; }
public List<V> Values { get; set; }
public List<Node> Children { get; set; }
/// <summary>
/// 向节点内部按照大小顺序插入一个元素,
/// </summary>
/// <param name="key"></param>
/// <param name="value"></param>
public void Insert(K key, V value)
{
var result = false;
for (var i = 0; i < Keys.Count; i++)
{
var compareValue = key.CompareTo(Keys[i]);
if (compareValue < 0)
{
Keys.Insert(i, key);
Values.Insert(i, value);
result = true;
break;
}
else if (compareValue == 0)
{
throw new Exception();
}
}
if (!result)
{
Keys.Add(key);
Values.Add(value);
}
}
public Node()
{
Keys = new List<K>();
Values = new List<V>();
Children = new List<Node>();
}
}
private int _level;
//单个节点包含key值数量的最小值(除了根节点外)
private int _minKeysCount;
private Node _first;
/// <summary>
/// B树初始化
/// </summary>
/// <param name="level">表示单个节点包含的最大Key值数量</param>
public BTree(int level)
{
_level = level;
_minKeysCount = (int)(Math.Ceiling(_level / 2.0) - 1);
}
}
BTree中定义的_level表示树的阶数,_minKeysCount表示单个节点关键字最小数目
Node表示B树中的一个节点,包含多个关键字和对应的Value值,还包含子节点的引用
插入节点
public void Insert(K key, V value)
{
if (_first == null)
{
_first = new Node();
_first.Insert(key, value);
}
else
{
var current = _first;
Insert(current, key, value);
}
}
private void Insert(Node current, K key, V value)
{
//如果当前节点是叶子节点,则直接插入到叶子节点,再看是否叶子节点需要分裂
if (current.Children.Count == 0)
{
if (current.Keys.Count > _level)
{
return;
}
current.Insert(key, value);
if (current.Keys.Count == _level)
{
Bubble(current);
}
}
else
{
//如果当前节点不是叶子节点,找出大于当前Key值的最小key对应的索引,找到对应的子节点,进行递归,直到找到最终的叶子节点
int childIndex = current.Keys.Count;
for (var i = 0; i < current.Keys.Count; i++)
{
var compareValue = key.CompareTo(current.Keys[i]);
if (compareValue < 0)
{
childIndex = i;
break;
}
else if (compareValue == 0)
{
throw new Exception();
}
}
current = current.Children[childIndex];
Insert(current, key, value);
}
}
/// <summary>
/// 冒泡
/// 当当前结点的个数等于阶数的时候,就需要把当前结点的最中间的关键字放到父结点中去,
/// 当前结点分裂成两个结点,小于中间结点的是左结点,大于中间结点的右结点,都作为子结点节点加到当前结点的父结点上面去,
/// 因为默认左结点的parent是父结点,所以只需要加入右结点
/// 然后再判断当前结点是否有子结点,如果有子结点 子结点个数必定超过了阶数(因为子结点的个数总是比当前结点的关键字数大1)
/// 若有子结点 则还需要把子结点分成两部分 一部分成为左结点的子结点 另一部分成为右结点的子结点 分界点就是当前结点最中间关键字所在位置
/// 然后递归执行,把关键字放到父结点中后,判断父结点是否也需要冒泡分裂
/// </summary>
/// <param name="current"></param>
private void Bubble(Node current)
{
var middleIndex = (current.Keys.Count - 1) / 2;
var middleKey = current.Keys[middleIndex];
var middleValue = current.Values[middleIndex];
var newRightChild = new Node();
newRightChild.Parent = current.Parent;
for (var i = middleIndex + 1; i < current.Keys.Count; i++)
{
newRightChild.Keys.Add(current.Keys[i]);
newRightChild.Values.Add(current.Values[i]);
}
var newLeftChild = current;
var count = newLeftChild.Keys.Count - middleIndex;
newLeftChild.Keys.RemoveRange(middleIndex, count);
newLeftChild.Values.RemoveRange(middleIndex, count);
for (var i = middleIndex + 1; i < current.Children.Count;)
{
var temp = current.Children[i];
newRightChild.Children.Add(temp);
temp.Parent = newRightChild;
newLeftChild.Children.RemoveAt(i);
}
if (current.Parent == null)
{
current.Parent = new Node();
_first = current.Parent;
_first.Children.Add(newLeftChild);
_first.Children.Add(newRightChild);
newLeftChild.Parent = _first;
newRightChild.Parent = _first;
}
else
{
current.Parent.Children.Add(newRightChild);
}
current = current.Parent;
current.Insert(middleKey, middleValue);
if (current.Keys.Count >= _level)
{
Bubble(current);
}
}
查找节点
private Node Find(K key, out int index)
{
index = -1;
if (_first == null)
{
return null;
}
var current = _first;
while (true)
{
var childIndex = current.Keys.Count;
for (var i = 0; i < current.Keys.Count; i++)
{
var compareValue = key.CompareTo(current.Keys[i]);
if (compareValue < 0)
{
childIndex = i;
break;
}
else if (compareValue == 0)
{
index = i;
return current;
}
}
if (current.Children.Count > 0)
{
current = current.Children[childIndex];
}
else
{
return null;
}
};
}
public bool ContainsKey(K key)
{
return Find(key, out int index) != null;
}
删除节点
public void Remove(K key)
{
var current = Find(key, out int index);
if (current == null)
{
return;
}
current.Keys.RemoveAt(index);
current.Values.RemoveAt(index);
BorrowFromChild(current, index);
}
/// <summary>
/// 删除节点后,如果当前节点key的数目少于_minKeysCount,需要向子节点借一个key (类似于算术减法,低位数不够向高位借)
/// </summary>
/// <param name="current"></param>
/// <param name="index"></param>
private void BorrowFromChild(Node current, int index)
{
if (current.Children.Count == 0)
{
if (current.Keys.Count < _minKeysCount)
{
BorrowFromParent(current);
}
return;
}
var leftChild = current.Children[index];
var rightChild = current.Children[index + 1];
if (rightChild.Keys.Count > _minKeysCount)
{
var childIndex = 0;
current.Keys.Insert(index, rightChild.Keys[childIndex]);
current.Values.Insert(index, rightChild.Values[childIndex]);
rightChild.Keys.RemoveAt(childIndex);
rightChild.Values.RemoveAt(childIndex);
}
else
{
//remove
var childIndex = leftChild.Keys.Count - 1;
current.Keys.Insert(index, leftChild.Keys[childIndex]);
current.Values.Insert(index, leftChild.Values[childIndex]);
leftChild.Keys.RemoveAt(childIndex);
leftChild.Values.RemoveAt(childIndex);
if (leftChild.Keys.Count < _minKeysCount)
{
BorrowFromChild(leftChild, childIndex);
}
}
}
/// <summary>
/// 叶子节点key的数目不够时,需要向父节点借
/// </summary>
/// <param name="current"></param>
private void BorrowFromParent(Node current)
{
var parent = current.Parent;
if (parent == null)
{
//当前结点为根结点的话 不需要操作
return;
}
var index = parent.Children.IndexOf(current);
if (index > 0)
{
//若有左边兄弟结点
var leftSibling = parent.Children[index - 1];
var leftKeysIndex = leftSibling.Keys.Count - 1;
if (leftKeysIndex >= _minKeysCount)
{
current.Keys.Insert(0, parent.Keys[index-1]);
current.Values.Insert(0, parent.Values[index-1]);
parent.Keys[index-1] = leftSibling.Keys[leftKeysIndex];
parent.Values[index-1] = leftSibling.Values[leftKeysIndex];
leftSibling.Keys.RemoveAt(leftKeysIndex);
leftSibling.Values.RemoveAt(leftKeysIndex);
return;
}
}
if (index < parent.Children.Count - 1)
{
var rightSibling = parent.Children[index + 1];
if (rightSibling.Keys.Count > _minKeysCount)
{
current.Keys.Add(parent.Keys[index]);
current.Values.Add(parent.Values[index]);
parent.Keys[index] = rightSibling.Keys[0];
parent.Values[index] = rightSibling.Values[0];
rightSibling.Keys.RemoveAt(0);
rightSibling.Values.RemoveAt(0);
return;
}
}
//如果左右两边兄弟结点都不满足条件 判断是否有左边兄弟结点,如果有则和左边兄弟结点合并 没有 和右边兄弟结点融合
if (index > 0)
{
MergeToLeft(parent, parent.Children[index - 1], current);
}
else
{
MergeToLeft(parent, current, parent.Children[index + 1]);
}
if (parent.Keys.Count < _minKeysCount)
{
if(parent == _first)
{
//如果是根结点
if(parent.Keys.Count == 0)
{
_first = current;
current.Parent = null;
}
}
else
{
BorrowFromParent(parent);
}
}
}
private void MergeToLeft(Node parent, Node left, Node right)
{
var index = parent.Children.IndexOf(left);
left.Keys.Add(parent.Keys[index]);
left.Values.Add(parent.Values[index]);
parent.Keys.RemoveAt(index);
parent.Values.RemoveAt(index);
left.Keys.AddRange(right.Keys);
left.Values.AddRange(right.Values);
left.Children.AddRange(right.Children);
parent.Children.Remove(right);
}
以上代码均为原创分享,若大家认为有不妥的地方,烦请留言指出,在下感激不尽
也希望各位能够多多分享自己写的东西,共同进步


 浙公网安备 33010602011771号
浙公网安备 33010602011771号