线代学习笔记
线代学习笔记
1.向量部分
张成空间:就是向量构成的空间
线性相关:一个向量,他的存在与否不会影响张成空间,则称为线性相关。
线性无关:就是缺一不可。
基:向量空间的一组基是张成该空间的一个线性无关向量集。
矩阵乘法:
以前学矩阵快速幂什么的时候以为自己懂了,实际上没弄清楚本质。
这里写矩阵似乎有点麻烦。
先说算法:
对于 \(A*B=C\)
\(C_{i,j} = A rowi * B colomn j=\sum{a_{ik}*b_{kj}}\)
很明显,答案矩阵 \(C\) 的行数由 \(A\) 决定,列数由 \(B\) 决定
矩阵式可以切割的。
所以,也可以不用 \(\sum\),用一行乘一列。
同样,你还可以分块拆,把大矩阵拆成一块一块的,同样对于每一小块,你可以矩阵乘法。(递归预定)
单位矩阵: 从左上到右下的对角线为1,其余为0。这样乘起来不会改变值。
逆:
对于矩阵 \(A\), \(A * A^{-1}=I\),\(I\) 是单位矩阵,则 \(A^{-1}\) 为 \(A\) 的逆。
显然,有2种逆,左逆和右逆。
左逆就是 \(A^{-1}\) 在左边,右逆就是右边。
对于方阵,左右逆相等(似乎是剧透的,以后再补)
如果不存在逆,就是 奇异矩阵,反之,就是 非奇异矩阵
举个奇异矩阵例子:
有趣的证明:如果 对于 非零的 \(x\), 仍然有 \(Ax=0\),则 \(A * A^{-1}*x=0\),则 \(x=0\),而上述矩阵显然有
所以为奇异矩阵。(有意思捏)
当然,他行列式为 0 也可以判断。
Gauss-Jordan
用高斯消元的方法,将左侧变为单位矩阵,右侧增广就是 逆矩阵。
(真的nb)
为什么呢
因为我们使用消元矩阵 \(E\),\(EA=I\), 则 \(E=A^{-1}\)
LU 分解
A 的 LU 分解 就是把 A 分解为 下三角矩阵 L,和上三角矩阵U
转置
就是对过去
M 一定是对称矩阵(就是和转置相等的)
很好证明,就是求下 \(M^T\) 而已
伴随矩阵


来自知乎:https://zhuanlan.zhihu.com/p/420215318
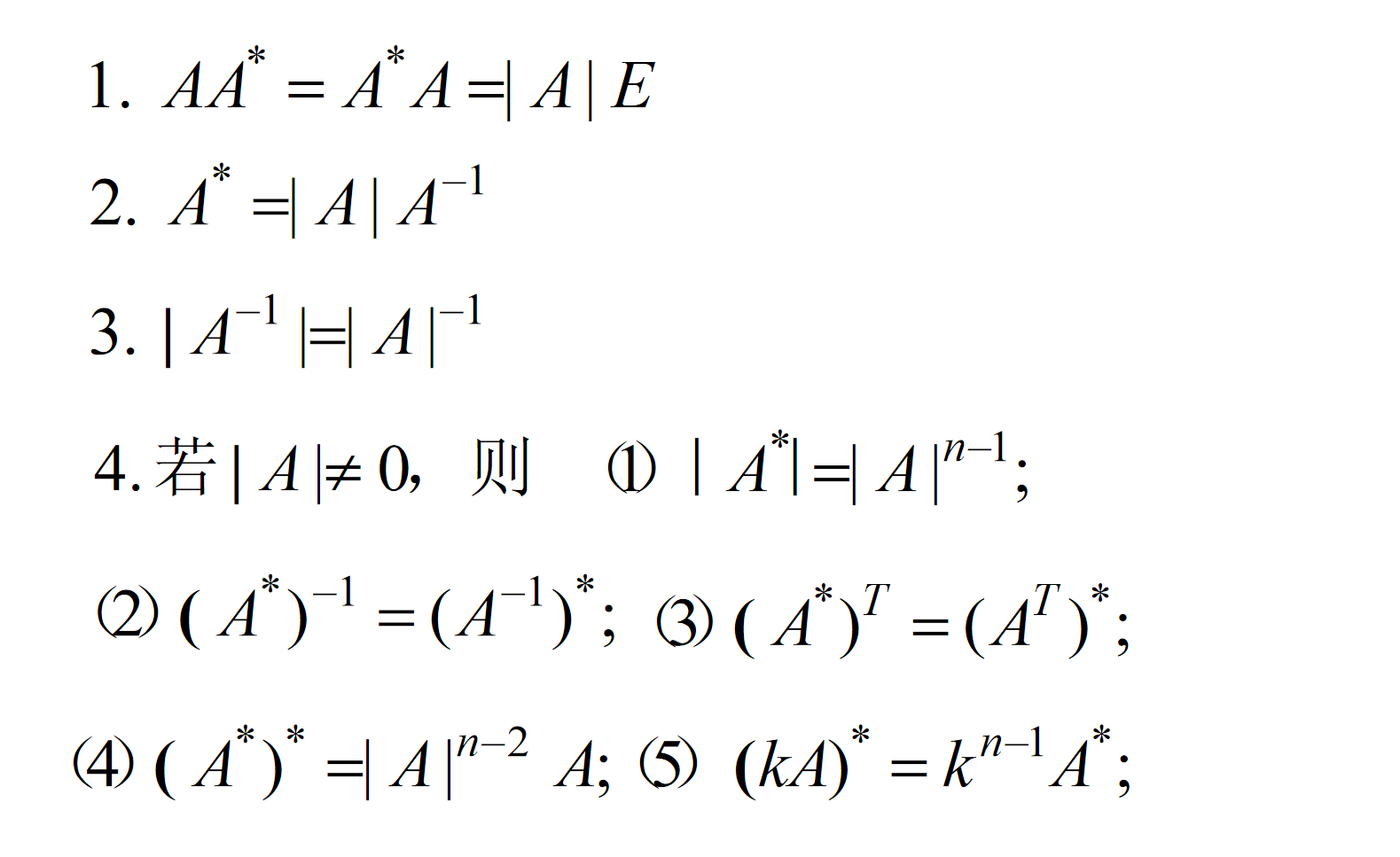


 浙公网安备 33010602011771号
浙公网安备 33010602011771号