[原创]什么是光的透过率？为什么透过的光的能量与电场强度的平方而不是一次方或者三次方有关？
本文参考Optics这本书的 4.6 The Electromagnetic Approach小节及其截图。不要被英语吓到，他们只不过是另一种描述问题的方式，无论是英语日语西班牙语，所描述的事情的本质是同一个，所描述的自然界的规律是同一个。但他们描述的过程是按照国外文化的习惯和思考问题的方式去描述的，我们在理解这些本质以后，应当用我们自己文化的思考习惯和看待问题的方式重新看待这些本质，从我们自己文化的视角重新感受这些自然界的规律，如果有需要，还要重新描述这些自然界的规律。
透过率，英文为transmittance，本身就是从能量的角度来定义的，含义是透过的能量比例有多少。为什么透过一个透明物体的光的能量与电场强度的平方有关系呢？
如图，其中两种介质的界面处的面积用A来表示，下标i为incident，入射的意思，下标r为reflect，反射的意思，外国人用他们的语言来做标记，我们也可以用汉语来标记，比如 光强度入射光，或者直接写作入射光的光强度，标记本身是什么样的无所谓，只不过是一种描述事物本质的不同表达形式而已，关键是要理解这种表达具体所指的是什么。$ \theta _{i} $是入射角，$ \theta _{r} $是反射角。
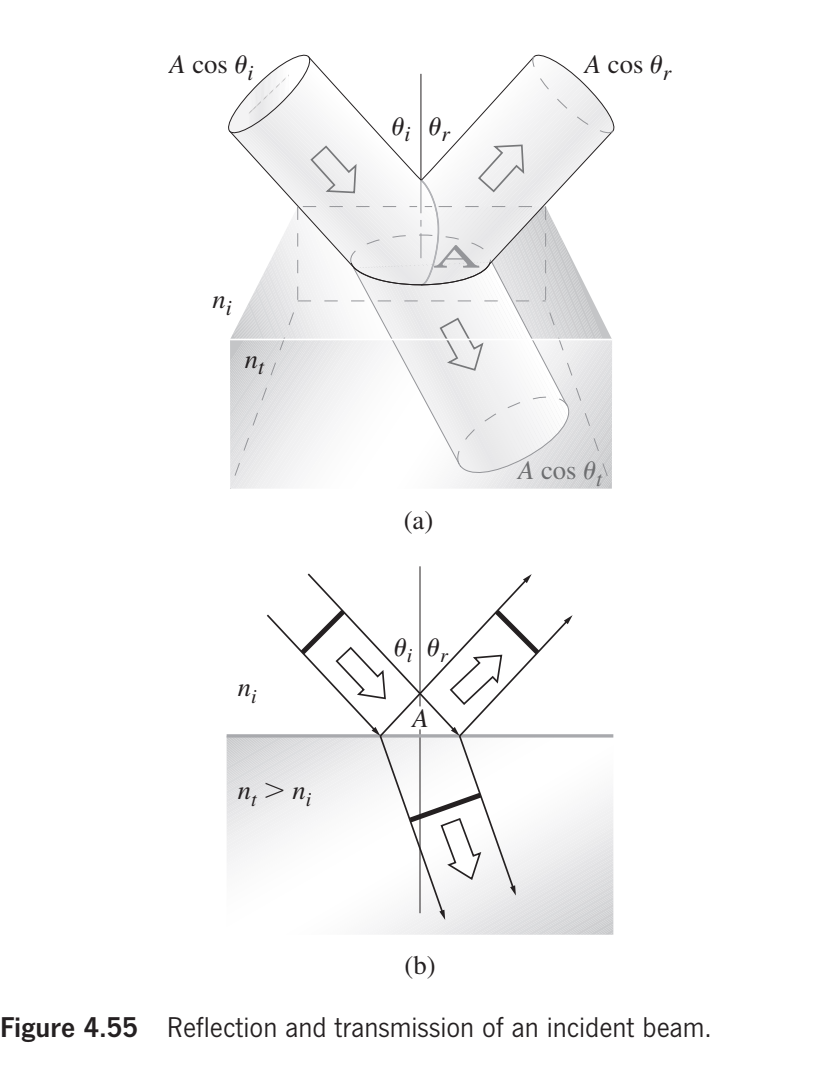
根据三角关系，垂直于入射光平面的面积为A乘以$ \cos \theta _{i} $，即为$ A\cos \theta _{i} $,同理垂直于反射光平面的面积为$ A\cos \theta _{r} $。
现在面积有了，那么单位面积上光的能量有多大呢？Optics这本书里用$ I_{i} $，$ I_{r} $，$ I_{t} $表示垂直于入射光平面上光的能量密度，垂直于反射光平面上光的能量密度，垂直于折射光平面上光的能量密度。书中用词是flux density，通量，单位时间内通过的量。 字母I，Intensity，the strength of sth, for example light, that can be measured 强度，下标i r t的含义上面已经讲过。
那么透过率，transmittance，用这个单词的首字母T表示，
$ T=\frac{I_{t}A\cos \theta_{t}}{I_{i}A\cos \theta_{i}}=\frac{I_{t}\cos \theta_{t}}{I_{i}\cos \theta_{i}} $
I等于什么呢？
$ I=\left \langle S \right \rangle_{T}=\frac{c\varepsilon_{0}}{2}E_{0}^{2} $
这个公式怎么来的呢？我们先来看看3.3 Energy and Momentum这一小节。电磁波的传播过程也是能量的传播过程，那么他经过的空间里能量的密度是多少呢？先来看看平行板电容器两个极板中间的能量密度的计算公式：
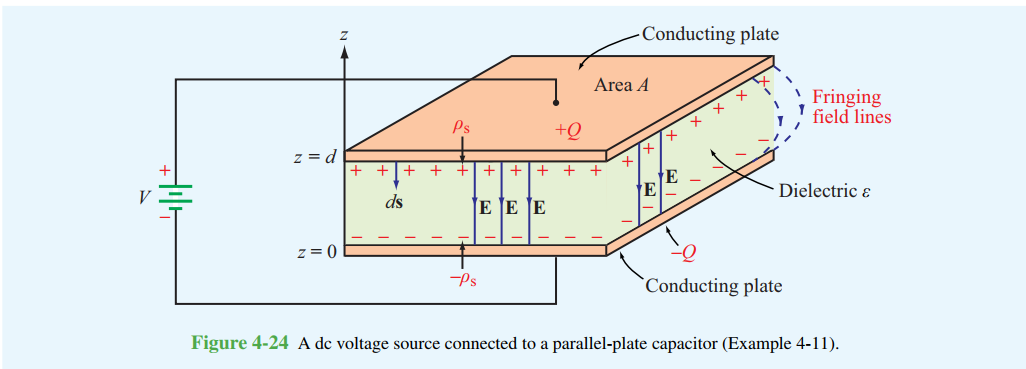截图来自于《Fundamentals of Applied Electromagnetics》-Fawwaz T. Ulaby, Umberto Ravaioli -Prentice Hall (2014)
假设一个平行板电容器平行板的面积为A，两个板距离为d，那么电容的大小C为$ C=\varepsilon _{0}A/d $，将平行板电容器两端从0达到电压为V时，电源所做的功为$ \frac{1}{2}CV^{2} $（具体计算过程参考《Fundamentals of Applied Electromagnetics》4-10 Electrostatic Potential Energy
这一小节），而V=E乘以d。假设电源所做的功储存在平行板电容器中间的空间中，空间的体积为A乘以d，那么空间里能量的密度为能量密度$ =\frac{\frac{1}{2}CV^{2}}{Ad} $，将刚才提到的C和V代入，得到能量密度$ =\frac{(\frac{1}{2}) (\varepsilon _{0}A/d)(Ed)^{2}}{Ad} $，整理后得到能量密度=$ \frac{\varepsilon _{0}}{2} E^{2} $。
类似的，在磁场强度为B的区域的能量密度，以螺线管为例，如下图，螺线管中间为空气，截面积为A，螺线管长为l，单位长度内电线绕着螺线管转了n圈，假设螺线管的电感为L，$ L=\mu _{0} n^{2} l A $当电流通过螺线管从0到电流$ I $时，电源所做的功为$ \frac{1}{2}LI^{2} $（具体计算过程参考《Fundamentals of Applied Electromagnetics》5-8 Magnetic Energy
节 ），此时的磁场强度为$ B = \mu_{0} n l $，那么螺线管中间空间的体积为$ A l $,将L和I代入，得到磁场强度为B时能量密度为$ \frac{ (\frac{1}{2}) L I ^{2} }{Al} $，将L和I代入化简，得到能量密度=$ \frac{ \frac{1}{2}(\mu _{0} n^{2} lA)(B/ \mu _{0} n)^{2} }{ A l} $，简化后得到能量密度=$ \frac{1}{2\mu _{0}}B^{2} $
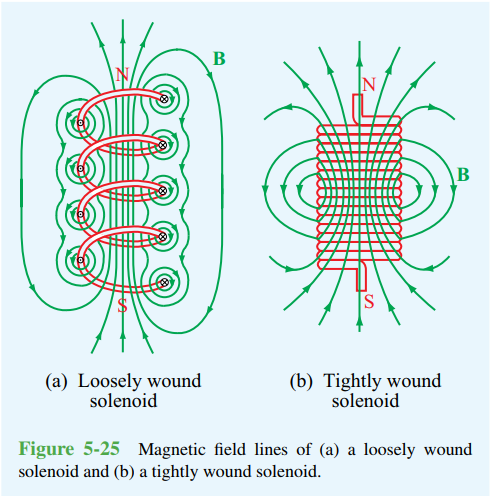截图来自于《Fundamentals of Applied Electromagnetics》-Fawwaz T. Ulaby, Umberto Ravaioli -Prentice Hall (2014)
因为由平面波推导出来$ E=cB $， $ c=1/\sqrt{\varepsilon _{0}\mu _{0}} $（Optics 3.3节提到的，公式怎么来的，稍后补充），代入以后得到在一个传播的电磁场中，电场的能量密度=磁场的能量密度，所以电磁波经过的空间里总的能量密度=$ \varepsilon _{0}E^{2} $，或者等于$ \frac{1}{\mu _{0}}B^{2} $。假如在这里用u来表示总的能量密度。
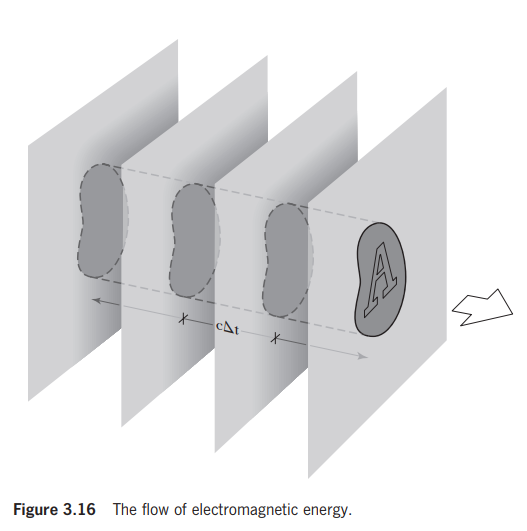
在电磁波传播过程中，能量密度是随着时间的变化而变化的，因为E和B是随着时间的变化而变化的。假设用S来指代单位时间内穿过单位面积的能量。如图（Optics这本书的 3.3.1 The Poynting Vector
），假设电磁波以速度c沿着垂直于面积为A的方向传播，经过时间$ \Delta t $经过的空间的体积为$ c\Delta tA $，乘以空间中的能量密度，那么在时间$ \Delta t $内经过面积为A的能量大小为$ uc\Delta tA $，那么单位时间单位面积上穿过的能量为$ \frac{uc\Delta tA}{\Delta tA}=uc $，刚才已经算出来能量密度u，代入其中得到，单位时间内穿过单位面积的能量S=$ \frac{1}{\mu _{0}}EB $，这是某个电磁波电场强度为E磁场强度为B的电磁波在单位时间单位面积内传播的能量。
如果用向量来表示， $ \vec{S}=\frac{1}{\mu _{0}}\vec{E}\times \vec{B} $，或者$ \vec{S}=c^{2}\varepsilon _{0}\vec{E}\times \vec{B} $，方向就是沿着电磁波传播的方向，因为$ \vec{B} $和$ \vec{E} $正好垂直，所以叉乘过程中的sinθ值为1.这个向量就是the Poynting vector，所谓的“坡印亭矢量”，用方向和大小描述了某个电磁波单位时间单位面积内传播的能量。比如来了一个电磁波，问你这个电磁波的传播方向和能量大小有多少啊，你告诉他电磁波往哪里传播，能量多少，就可以用这个量来描述这个电磁波。
实际电场和磁场随着时间的变化和距离的变化公式为：
$ \vec{E}=\vec{E_{0}}\cos (\vec{k}\cdot \vec{r}-\omega t) $
$ \vec{B}=\vec{B_{0}}\cos (\vec{k}\cdot \vec{r}-\omega t) $
关于$ (\vec{k}\cdot \vec{r} $这种形式是平面波的表达形式，可以参考本博文讲平面波的文章。
那么$ \vec{S}=c^{2}\varepsilon _{0}\vec{E_{0}}\times \vec{B_{0}}\cos ^{2}(\vec{k}\cdot \vec{r}-\omega t) $。
书中用尖括号加下标的形式$ \left \langle f\left ( t \right ) \right \rangle_{T} $表示一个函数f(t) 的值在时间段T内的均值。那么$ \left \langle S \right \rangle_{T} $的均值为$ \vec{S}=c^{2}\varepsilon _{0}|\vec{E_{0}}\times \vec{B_{0}|}\left \langle \cos ^{2}(\vec{k}\cdot \vec{r}-\omega t) \right \rangle $，即里面cosXXX在时间T内的均值
那么cosXXX在时间T内的均值为多少呢？为$ \frac{1}{2} $.直观而言如下图所示(还有一种理解方法，附在了本文结尾)
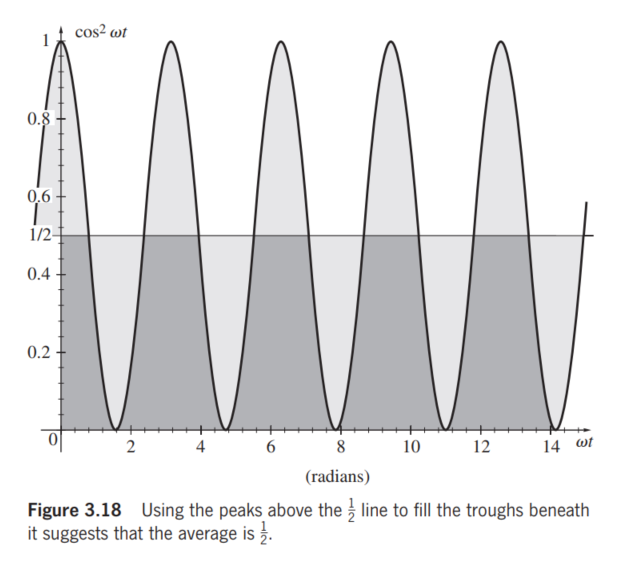
所以$ \left \langle S \right \rangle_{T}=\frac{c^{2}\varepsilon _{0}}{2}|\vec{E_{0}}\times \vec{B_{0}|} $，也就是说对于一个磁场强度为B电场强度为E的电磁波而言，一段时间内（只不过这段时间与电磁波本身的能量变化周期相比远大于其变化周期）传输的能量均值为此。光也是一种电磁波，那么一段时间内光传输的能量均值可以理解为 $ I\equiv \left \langle S \right \rangle_{T}=\frac{c^{2}\varepsilon _{0}}{2}|\vec{E_{0}}\times \vec{B_{0}|}=\frac{c\varepsilon _{0}}{2}E_{0}^{2} $，这也就是为什么穿透的光的能量密度与电场强度的平方成正比，其实也与磁场强度的平方成正比。
因为电场被认为可以更有效的施加力量，对带点体做功（与磁场比起来），所以把电磁波的电场强度成为光学部分。怕翻译的不会，原文贴到下面了。
在3.3.2 Irradiance这一节中有较为详细的讲解。课本上说如何衡量照射到某个面上的光的量呢？可以发明或者说建立一个概念——irradiance，a measurement of the amount of light that comes from sth 中文翻译为辐照读，辐射照明的强度。含义是单位时间内单位面积上照射到的能量。如果能量分布不是平均的，那就应该是做了平均以后单位时间内单位面积上照射到的能量。
关于求解$ e^{i\omega t} $在时间t-T/2到t+T/2内的均值, 有公式$ \left \langle e^{i\omega t}\right \rangle_{T}=\frac{1}{T}\int_{t-T/2}^{t+T/2}e^{i\omega t}dt=\frac{1}{T}\frac{1}{i\omega}e^{i\omega t}|_{t-T/2}^{t+T/2}=\frac{1}{i\omega T}e^{i\omega t}(e^{i\omega T/2}-e^{-i\omega T/2}) $ （Optics的Averaging Harmonic Functions
这一小节中讲到的）
根据Optics的2.5 The Complex Representation 小节有讲到$ \sin \theta =\frac{e^{i\theta }-e^{-i\theta }}{2i} $，那么在这个公式里$ \theta =\frac{\omega T}{2} $.那么化简得到$ \left \langle e^{i\omega t}\right \rangle_{T}=( \frac{\sin \omega T/2}{\omega T/2} )e^{i\omega t} $,我们把$ ( \sin u)/u $记作sinc u，这里$ u=\omega T/2 $。将两边都按照欧拉公式替换，那么得到$ \left \langle \cos \omega t \right \rangle_{T}=（sinc \space u）\cos \omega t $, $ \left \langle \sin \omega t \right \rangle_{T}=（sinc \space u）\sin \omega t $.
$ ( \sin u)/u $的函数图像如下：用到的软件GeoGebra可以免费使用
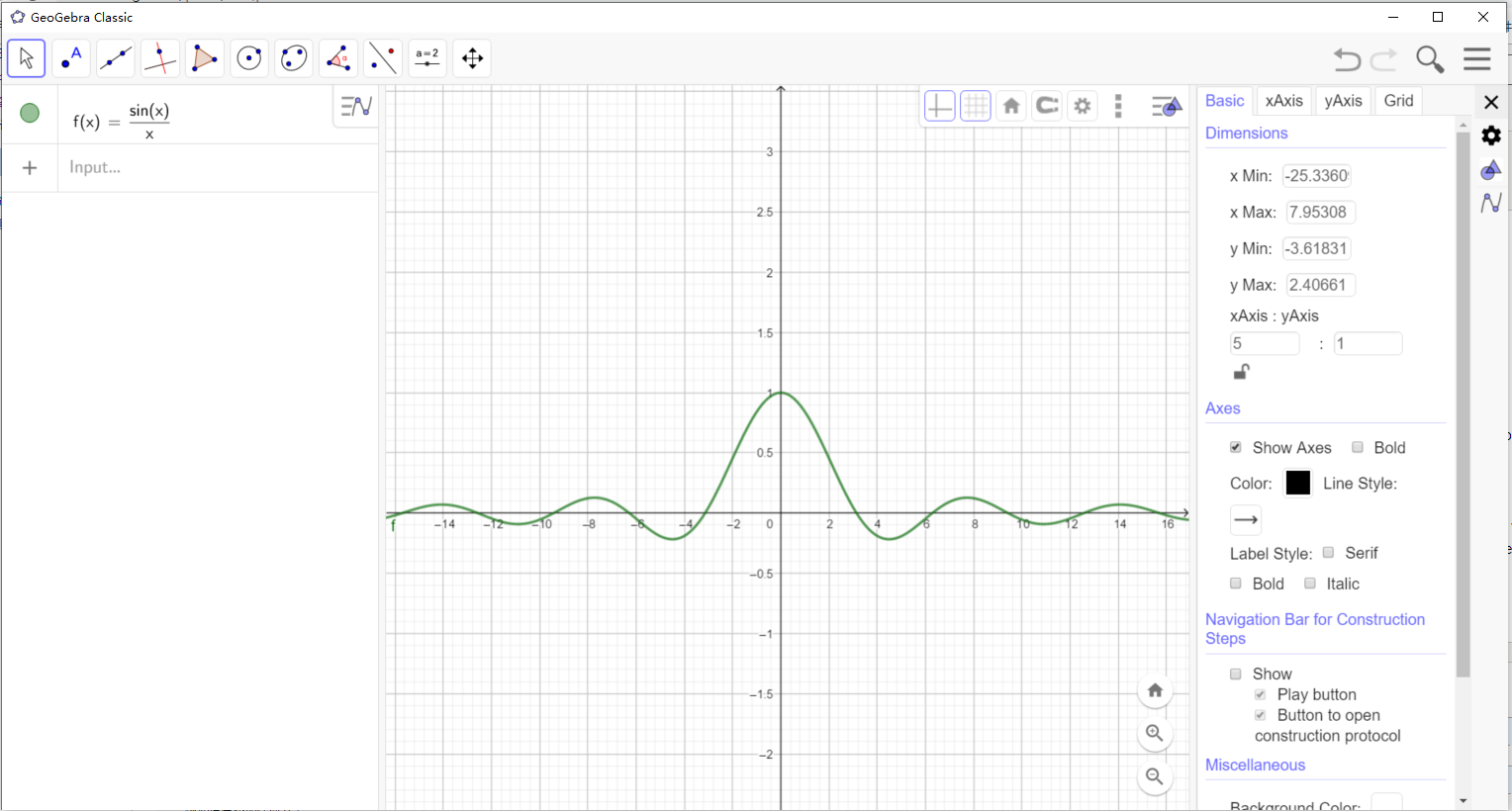
注意观察可以发现在当x=$ \pi $,$ 2 \pi $,$ 3 \pi $时函数值为0
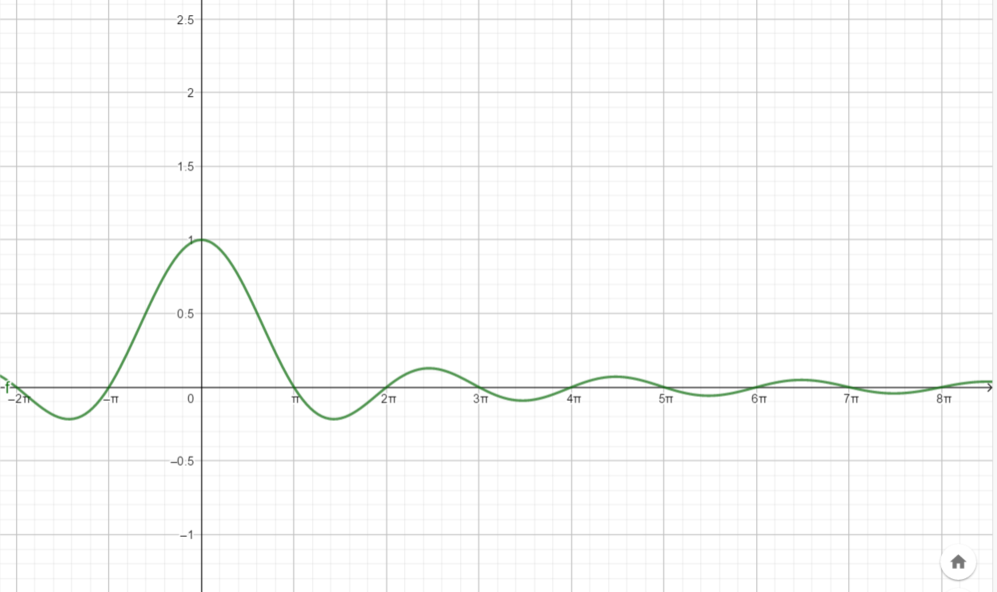
那么经过计算（Optics这本书留在了Problem 3.16）
$ \left \langle \cos^{2} \omega t\right \rangle_{T}=\frac{1}{2}[1+sinc \space \omega T\cos 2\omega t] $，当T足够大时，$ \left \langle \cos^{2} \omega t\right \rangle_{T}=1/2 $
