[原创]当我们看到微积分中的那些符号时我们联想到了什么?
微积分的符号系统,或者说记号系统,英文教材中称之为notation,用来标记某种操作,某一系列的操作或者某个概念,这些符号比较让人难以想象到对应的具体操作是什么,因为这些符号都是从国外的文化中引申得来的,语言、文字和符号的含义都深深的刻上了国外文化的痕迹,直接看这些符号和他所代表的含义,对于我们而言难免有陌生不合逻辑的感觉,因为看到一个符号所联想到的文化和情感,看到一个符号所引起的直觉就不一样,从而对理解这些记号系统所代表的具体的数学运算产生了阻碍。当这些记号系统不能成为精确的表达、提醒和记忆的辅助,反而成为了理解的障碍的时候,应该怎么做呢?谁来改进这些符号系统呢?当看到某种数学表达形式的时候,要想到的是这种公式意味着什么样的操作,这样有助于理解数学公式所想要表达的事情的本质。平常有整理一些符号对应的含义是什么,罗列在下面,希望从符号到符号所指代的含义这一步花费的时间减少一些。文章中的截图大多来自于《Thomas Calculus》第14版,并需要读者稍微有一点微积分的了解。3Blue1Brown在b站上有关于微积分的视频,讲的挺好的,可以去看看~
本文时不时的会补充添加
哪个地方说的不对欢迎大家批评指正~毕竟一个人的理解有限,众人拾柴火焰高~
1、积分符号
 比如当看到积分的符号$ \int $,就是一个拉长的s,英文单词sum(求和)的简写。以单独一个变量(或者就叫做“单变量”)的积分为例,如下图5.10。把自变量分割成几十段,每段的长称之为$ \Delta x $,每段$ \Delta x $对应于函数$ f\left ( x \right ) $的一小段曲线,如下图橘黄色线段所示,把每一段曲线下方的面积求出来,然后累加求和,就是函数$ f\left ( x \right ) $与x轴所包围的区域的面积。那么单独的一段曲线下方的面积怎么求呢,近似,找到一个方法近似。我以这段中的任何一个值$ x_{1} $对应的函数值$ f\left ( x_{1} \right ) $ 作为这块面积的高度,求得这块的面积。如下图所示。好像还有一小段曲线下的面积没有被计算在内哎?没关系,这块我们不要了~这样把每一块都求出来,然后累加,这就是所谓的黎曼求和(Riemann sums),
比如当看到积分的符号$ \int $,就是一个拉长的s,英文单词sum(求和)的简写。以单独一个变量(或者就叫做“单变量”)的积分为例,如下图5.10。把自变量分割成几十段,每段的长称之为$ \Delta x $,每段$ \Delta x $对应于函数$ f\left ( x \right ) $的一小段曲线,如下图橘黄色线段所示,把每一段曲线下方的面积求出来,然后累加求和,就是函数$ f\left ( x \right ) $与x轴所包围的区域的面积。那么单独的一段曲线下方的面积怎么求呢,近似,找到一个方法近似。我以这段中的任何一个值$ x_{1} $对应的函数值$ f\left ( x_{1} \right ) $ 作为这块面积的高度,求得这块的面积。如下图所示。好像还有一小段曲线下的面积没有被计算在内哎?没关系,这块我们不要了~这样把每一块都求出来,然后累加,这就是所谓的黎曼求和(Riemann sums), 就可以近似求出函数与x轴所围成的面积。
就可以近似求出函数与x轴所围成的面积。

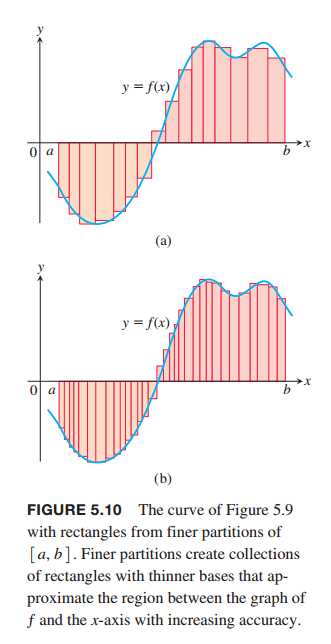 那么现在更进一步,前面说把自变量分割成几十段,当分的段数越来越多,越来越密时,刚才扔掉不要的部分所占的比例就会越来越少,如图5.10 (b),这个近似求得的面积就会接近真实的面积,无限逼近,以至于相等。把自变量分割成几十段,平均分割还是不平均分割?都没有关系,只要找到分成的这几十段中最大的一个,让最大的这个无限接近于0就好,也就是意味着分割的所有的段长度都无线接近于0,无限细密。这其实就是
那么现在更进一步,前面说把自变量分割成几十段,当分的段数越来越多,越来越密时,刚才扔掉不要的部分所占的比例就会越来越少,如图5.10 (b),这个近似求得的面积就会接近真实的面积,无限逼近,以至于相等。把自变量分割成几十段,平均分割还是不平均分割?都没有关系,只要找到分成的这几十段中最大的一个,让最大的这个无限接近于0就好,也就是意味着分割的所有的段长度都无线接近于0,无限细密。这其实就是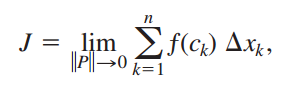 中的P。用$ \lim_{\left \| p \right \|\rightarrow 0} $ 表示所有的段长度都无线接近于0,无限细密,就是所谓的求极限的思想, 将积分的自变量的范围分割成多段,比如分割成n段,这些段长短不一,其中最长的那个称之为norm,英语里是norm of a Partition,用P来表示, 当最长的这一段都接近于0时,即为 ||P|| 接近于0时,说明我们的分割无线细了,那这个时候的累加($ \sum $,sigma求和,另一个符号,含义见下方截图,表示累加)会无限接近一个值,这个值就称之为积分的值,积分,英语为calculus,中文翻译成积分,累积各个部分。为什么用$ \Sigma $表示累加呢?因为这个字母在国外的文化中有加和的含义。这么写比较麻烦,Leibniz(莱布尼兹)使用了一种新的记号方式,,就是最开始截图的那种记号方式。教材中是这样说的
中的P。用$ \lim_{\left \| p \right \|\rightarrow 0} $ 表示所有的段长度都无线接近于0,无限细密,就是所谓的求极限的思想, 将积分的自变量的范围分割成多段,比如分割成n段,这些段长短不一,其中最长的那个称之为norm,英语里是norm of a Partition,用P来表示, 当最长的这一段都接近于0时,即为 ||P|| 接近于0时,说明我们的分割无线细了,那这个时候的累加($ \sum $,sigma求和,另一个符号,含义见下方截图,表示累加)会无限接近一个值,这个值就称之为积分的值,积分,英语为calculus,中文翻译成积分,累积各个部分。为什么用$ \Sigma $表示累加呢?因为这个字母在国外的文化中有加和的含义。这么写比较麻烦,Leibniz(莱布尼兹)使用了一种新的记号方式,,就是最开始截图的那种记号方式。教材中是这样说的

求解一个函数积分的时候,
应当想到的是一小段自变量区间乘以这一小段自变量区间里的函数值,求所有这样的值的和,也就是先分割,相乘,再累加。积分这个符号实际是由累加引申得到的。
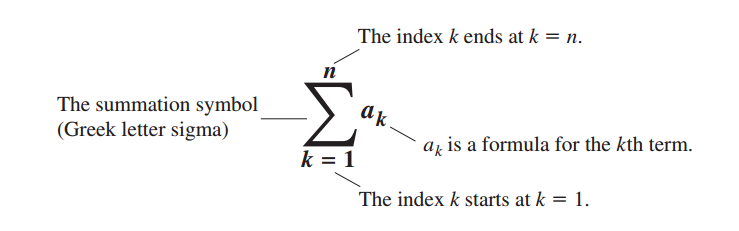
2、偏微分
任何一种名字,称呼,或者标记,都是为了代指一种具体的概念,某个操作,某一系列的操作当作一个整体,某个具体的事物等等等等,总之都是有具体的指代,哪怕这个指代的事物本身就是从更具体的事物抽象而来的。这样在跟别人交流的时候,就不必用实物来表达自己的想法,而只需要用名字,标记或者称呼来就可以了。比如当我说“我喜欢苹果”的时候,我没有必要拿出一个苹果给你看,然后说我喜欢“它”,而只需要直接说“我喜欢苹果”。再比如说求积分,你就知道我是将自变量分割成几百段几千段,每段取一个在其中的函数值乘以段的长度,然后累加……等等这一系列的操作。再比如我说求导,你就知道是找到两个点,求处对应的x和y值,用y的差值Δy除以x的差值Δx,当差值无限趋近于0时就是这一点的导数,直白点说就是斜率。只不过过去的科学家将求积分的过程越来越简化,只要做几步简单的操作就可以,不用做这么复杂了。
偏微分,英语是partial derivative,partial的意思是“部分,局部” not complete or whole,derivative就是微分了。因为一个函数变量很多,只对其中的一个变量求微分,那就是局部微分啦,只不过翻译时翻译成了偏微分,这个翻译并不是很有助于理解事情的本质。。。。。。。而用于表示偏微分的记号系统,也只是为了给出必要的信息,比如我对哪个函数求偏微分,求微分的变量是哪个自变量。
简单来说,偏微分就是多个自变量的函数,对其中一个自变量求微分。

当看到partial derivative时就是单独对这一个变量当作未知变量求导数,求导数就是求斜率,就是沿着这个未知变量方向变化时的变化速率
3、向量点乘然后积分

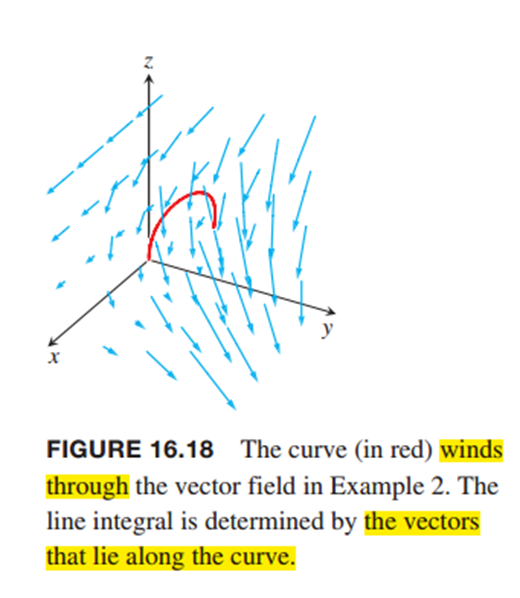
当看到向量点乘然后积分的时候,应该想到的是向量场沿着某条线的强度分布然后做一般的线积分

4、线积分

当看到线积分的时候要想到的是向量点乘的结果是向量沿着某个方向的分量,线积分就是沿着这条线这个方向的分量沿着线的作用的累加结果。圈圈表示闭合在一起的线
5、双重积分

当看到double integral时想到的应该是在一个面上的积分,即为一个函数的定义域是一个平面,值在z轴上,在这个平面上的函数值乘以一个定义域内的一小块面积,然后求和
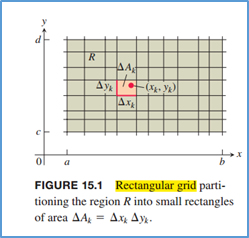
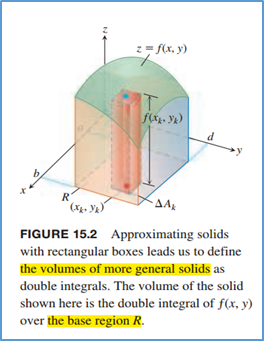
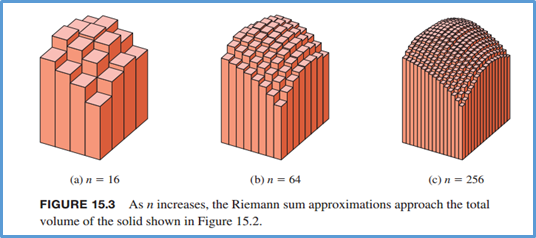

计算时双重积分的计算可以当作两次积分来计算

6、$ \oiint $符号

当看到左边这个符号的时候,表示两次积分,圆圈表示是一个闭合的面,点乘表示E沿着向量s的方向的分量,而向量s是垂直于面的向量
7、 把$ $展开以后得到右边的式子
把$ $展开以后得到右边的式子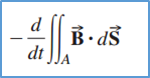
,当看到d/dt的时候想到的是某个量随着时间(或者随着别的什么变量)的变化率
8、向量场
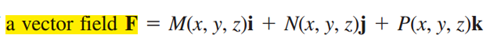
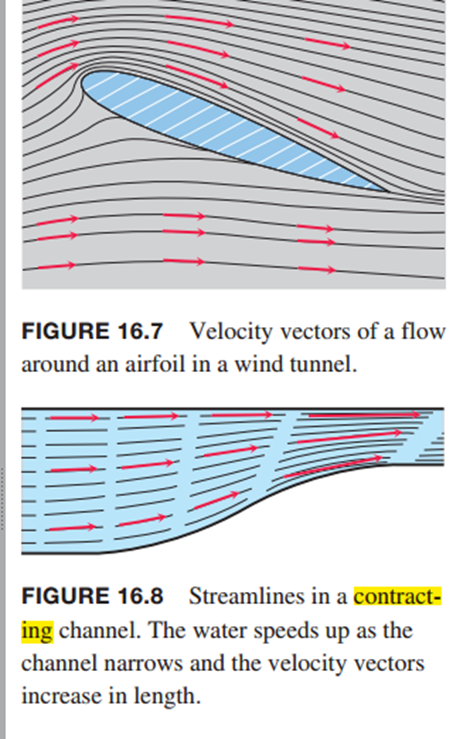
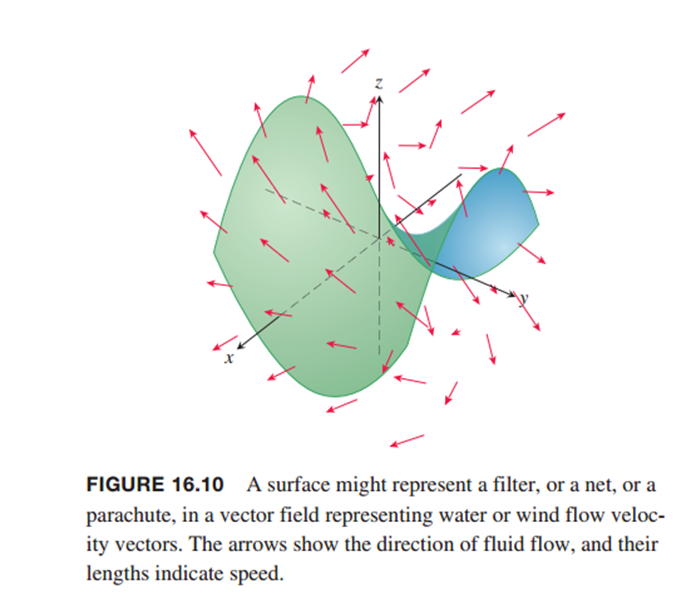
当看到vector field时想到的是如右图所示的样子
这个公式表示的是:给定x y z坐标,即给定某一个点时通过这个公式计算出该点处的向量,其中I j k 部分分别为这个向量x y z三个方向的分量。
那F如何表示一片区域的向量分布呢?当然是要输入x y z的取值范围,在x y z的取值范围下,每一个x y z的组合计算出来一个F,即为每一个x y z的组合计算出来一个点处的向量,然后各个点都有对应的x y z的组合,计算得到对应点处的向量

9 梯度符号 del operator
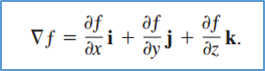 当看到gradient符号时想到的是函数在某个点处在三个方向上的变化率以向量的形式表现出来
当看到gradient符号时想到的是函数在某个点处在三个方向上的变化率以向量的形式表现出来
 以书中一个例子来讲解
以书中一个例子来讲解

10、cross product 叉乘
 当看到一个向量叉乘另一个向量的时候,要想到右手定则
当看到一个向量叉乘另一个向量的时候,要想到右手定则



11、沿着线的积分分开写的形式









