[读书笔记]电磁场中的高斯定律(Gauss's Law)的数学描述 Optics

电磁场中的高斯定律(Gauss's Law)的数学描述，截图来自于Optics 第5版，作者是Eugene Hecht

穿过一个封闭的曲面A的电场的通量（可以理解为净流量）的计算公式如下截图中所示，其中向量$  \vec{S} $是指向封闭曲面外侧的垂直于曲面A的单位向量，如图3.7所示。$ \vec{E}\cdot \vec{S} $是向量$  \vec{E} $在向量$  \vec{S} $方向上的分量乘以$  \vec{S} $的模，也就是说$  \vec{E} $垂直于$  \vec{S} $的分量不参与计算(点乘的概念)。因为他是在一个面上的积分，所以用两个积分符号$  \int\int  $，因为是闭合的曲面，所以在积分符号上画了一个圈，这些都是标记，用来做个标记说这是在一个面上的积分并且这个面是一个闭合曲面。下标A的意思是标记在名为A的曲面上积分。积分得到的量，电场强度的通量，用$ \Phi  $来表示。

         

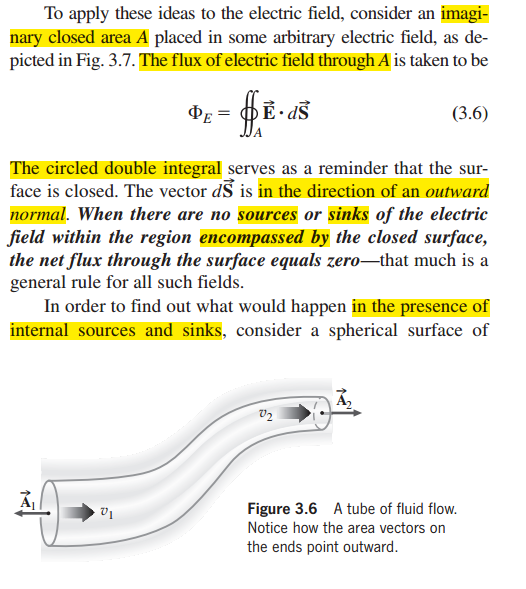
黑体字的含义是，如果封闭曲面内没有包含电场源（比如一个带正电的球或者一个带负电的球)，那么通过这个曲面的电场的净流量就是0。注意黑体字中的source和sink是从电场线的指向——指向周围和指向自己——的角度来说的，带正电的球电场线从球表面出发向四周发散，称之为source；带负电的球电场线从四周指向球的表面，仿佛电场线终结在球的表面一样，称之为sink，sink英语是水槽，下沉的意思），

 

 

 

 

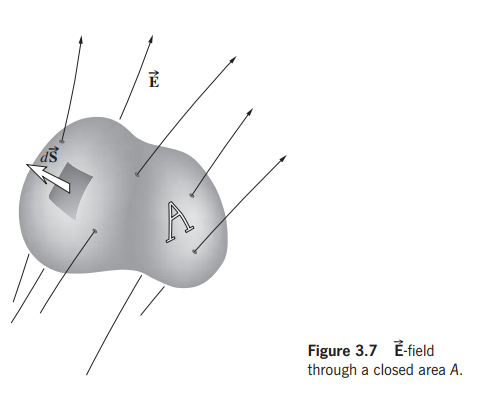
如下方截图所描述，假设一个半径为r的球包裹着一个点电荷，电荷量为q，点电荷在球的中心点，那么在球的表面上各点电场强度相同并且都垂直于球的表面，方向指向球的外部。球表面的面积为$  4\pi r^{2} $，根据库仑定律Coulomb law，球表面的电场强度为$  \frac{1}{4\pi \varepsilon _{0}}\frac{q}{r^{2}} $，计算得到的通过该曲面的电场的通量为$  \frac{q}{\varepsilon _{0}} $

 

 

 

 

 加入电荷在曲面所包裹的体积为V的空间内是连续分布的，密度为$  \rho  $，那么刚才计算得到的q应该用在三维空间上的积分求得，如下截图所示方程的右侧，就是求曲面所包裹的体积内包含的所有电荷的总量。

 

当曲面所包裹的体积非常小非常小，小到近似的看作一个点，那么通过这个曲面的电场强度的净流量除以曲面所包裹的体积，即为这个点的散度。

 

 

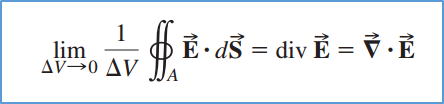
 如果方程3.7右侧也除以这个体积，得到的是曲面所包裹体积内单位体积的电荷，即为电荷密度$ \rho $ ，为下方截图所示公式，这就是Gauss's Law的微分形式。