Codeforces Round #842 (Div. 2)

D - Lucky Permutation(置换环)

题目大意
给定一个数组，该数组为1到n的全排列。
可以交换数组中两个不同元素的位置(无需相邻)
要使该数组的逆序对恰好为1，最少要多少次交换？

解题思路
逆序对为1的数组只可能是1到n按升序排列后交换相邻两元素得到的数组。
比如2,1,3,4,5...n就是逆序对为1的数组。

我们现在考虑根据原数组建立置换环。

置换环的思想就是：对每个元素，将其指向其排序后应该放到的位置，直到首位相接形成了一个环。
这里我们用元素的下标代表该元素。

比如对于数组[3,4,2,1]，若要将其变为1,2,3,4，其对应的环应该为：

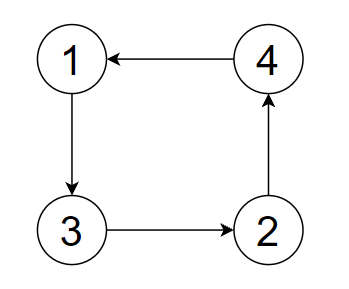
一号位上的元素是3，那么它应该放到3号位，所以有\(1\rightarrow 3\)，其它的元素按照相同的关系建边即可。

现在考虑交换数组中的元素对这个图有什么影响，交换3,2(即一号位的元素与三号位的元素)，数组变为[2,4,3,1]，图变为

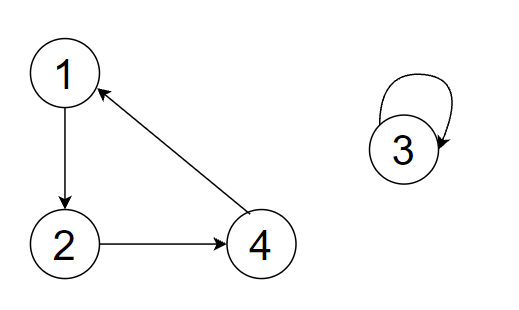
因为三号位的元素就是3，所以形成自环。
交换3,4(即一号位的元素与二号位的元素)，数组变为[4,3,2,1]，图变为

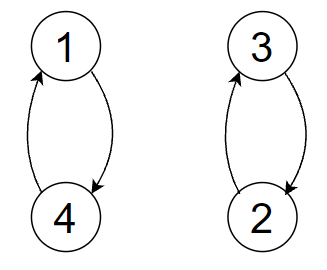
事实上，交换两个元素就是交换其对应点的出边。
我们的最终目的，就是将图变成这个样子：

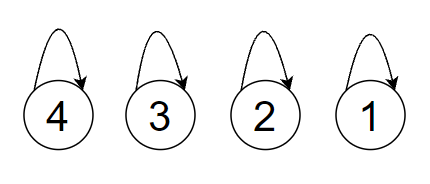
这就表示每个位置的元素都已归位。
要将一个图变成这样就是不断交换一条边的相邻两个节点，每次交换都能分离出一个节点形成自环，最少交换次数就是节点数减1。(为什么这样交换次数最少，证明起来好像还有点麻烦)

搞清楚交换元素与图的关系，问题就变得简单了。
刚刚是把数组变为1,2,3,4，现在变为逆序对位1的数组，比如变成2,1,3,4，对应的图应该是：

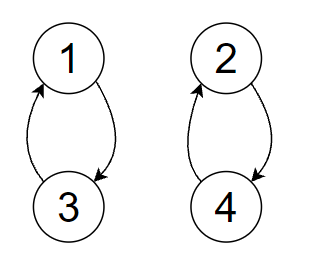
原来的元素1(其对应的位置是四号位)要回到一号位，现在要去二号位，元素2(三号位)原来要回到二号位，现在要去一号位。用\(x,\ y\)表示我们最后需要的逆序对，\(p_x,\ p_y\)表示他们在原数组中的位置，上图发生的变化就是在原图中断开\(p_x\rightarrow x\)与\(p_y\rightarrow y\)，
重连\(p_x\rightarrow y\)与\(p_y\rightarrow x\)。
容易发现若\(x,\ y\)在同一个环中，这种操作会使环的数目加1，
若不在同一个环中，会使环的数目减1。
而我们要使所有节点变为自环的操作数使节点数目-环的数目。
所以我们只需要先把原图求出来，再一次判断相邻元素是否在同一个环中即可。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int  N = 2e5 + 10;
int a[N];
void work()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i)
    {
        cin >> a[i];
    }
    int ans = n, ind = 1;
    vector<int> p(n + 1, 0);
    for (int i = 1; i <= n; ++i)
    {
        int t = a[i];
        if (p[t])
            continue;
        while (p[t] == 0)
        {
            p[t] = ind;
            t = a[t];
        }
        ++ind, --ans;
    }
    for (int i = 1; i < n; ++i)
    {
        if (p[i] == p[i + 1])
        {
            cout << ans - 1 << endl;
            return ;
        }
    }
    cout << ans + 1 << endl;
    return ;
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    int T;
    cin >> T;
    while (T--)
    {
        work();
    }
    return 0;
}