2-SAT
定义
2-SAT(Satisfiability)问题是这样的:有n个布尔变量,另有m个需要满足的条件,每个条件的形式都是“\(x_i\)为真/假或者\(x_j\)为真/假”(每条语句只有两个变量并且用或连接)。
我们的任务是判断对于n个布尔变量是否有合适的取值(0或1)来满足所有的条件。
解法
由于每种变量只有两种取值,我们用图中的两个点表示一个变量的取值,通常i号点表示第i个变量为真,i+n号点表示第i个变量为假。这两个点我们必须选择一个,因为一个变量必须要赋值且不能既赋真值又赋假值。
对于每一条语句(需要满足的条件),例如“\(x_1\)为真或者\(x_2\)为假”,那么我们可以得到两个推论。如果\(x_1\)为假那么\(x_2\)必为假,写成\(\bar{x_1}\to\bar{x_2}\);如果\(x_2\)为真那么\(x_1\)必为真,写成\(\bar{x_2}\to\bar{x_1}\)。这转化过后的两个条件在赋值的时候都要考虑,缺一不可。我们可以以此关系来建图。
将所有的语句建好图之后我们会得到一张有向图,如果我们选择了其中一个结点(一个结点就代表一种赋值方式),从这个节点开始,这条路径上的所有节点都要选择(我们就是用这种依赖关系来建图的)。
那么如何让判断有没有一种赋值方式(选择节点的方式)来满足所有的条件呢?很容易想到,假设我们选择\(x_1\)为真,沿着当前路径一直到底都没有遇到\(x_1\)为假这个结点,那么我们这次赋值是可行的。这就是蓝书上的做法。
例题:P4171 [JSOI2010] 满汉全席
#include<bits/stdc++.h>
using namespace std;
const int N=400+10;
const int M=4000+10;
int head[N],cnt;
struct{
int to,next;
}e[2*M];
int mark[N],s[N];
void add(int u,int v){
e[++cnt].to=v;
e[cnt].next=head[u];
head[u]=cnt;
}
void ini(){
memset(head,0,sizeof(head));
cnt=0;
memset(mark,0,sizeof(mark));
}
int k,n,m,c;
//标记结果保存在mark中
bool dfs(int u){
if(mark[u^1])return false;//当前结点的另一面也被标记则无解
if(mark[u])return true;//从u出发又回到了u,满足条件,返回
mark[u]=1;//标记
s[c++]=u;//记录当前标记过的点
for(int i=head[u];i;i=e[i].next)
if(!dfs(e[i].to))return false;
return true;
}
bool solve(){
for(int i=0;i<2*n;i+=2){
if(!mark[i]&&!mark[i+1]){//逐个考虑每个没有被标记的点
c=0;//用来记录这次共标记了多少个点
if(!dfs(i)){//先假设当前结点为真开始dfs
while(c)mark[s[--c]]=0;//失败的话撤销这次的标记
if(!dfs(i+1))return false;//真假标记都失败则无解
}
}
}
return true;
}
int main(){
scanf("%d",&k);
while(k--){
ini();
scanf("%d%d%*c",&n,&m);
char a,b,t;
for(int i=1;i<=m;++i){
int va=0,vb=0;
a=getchar();
while(isdigit(t=getchar()))va=va*10+t-'0';
b=getchar();
while(isdigit(t=getchar()))vb=vb*10+t-'0';
va--;vb--;
//printf("va:%d vb:%d\n",va,vb);
//这里为了后续转换方便用2*i表示i真,2*i+1表示i为假
add(2*va+(a=='m'),2*vb+(b=='h'));
add(2*vb+(b=='m'),2*va+(a=='h'));
}
if(solve())printf("GOOD\n");
else printf("BAD\n");
}
return 0;
}
下面考虑另一种做法。在一个SCC,如果我们选择了一个结点,这个SCC中的所有节点都要选择。如果代表某个变量的真假这两个节点在同一个SCC中,显然无论如何赋值都无法满足题意。反之,必定有解。
对于找到一组可行解,我们先将SCC缩成一个点,在求出新图的拓扑序。那么一个变量的真假这两个结点必定又不同的拓扑序(不然就在同一个SCC中了),我们选择拓扑序大的那个节点作为该变量的值。这是因为拓扑序小的节点可能存在到拓扑序大的结点的路径(注意这里是可能,这也说明了该问题的解不唯一),而反过来必然不会存在路径,所以这样选择不会发生冲突。
下面来证明若所有变量的真假两个节点都不在同一个SCC中,必然有解。
首先,按照这种方法建成的图是“对称”的。“对称”的意思是如果\(x_i\)与\(\bar{x_j}\)在同一个SCC中,那么\(\bar{x_i}\)与\(x_j\)也在同一个SCC中。
如果\(x_i\)与\(\bar{x_j}\)在同一个SCC中,那么存在\(x_i\)到\(\bar{x_j}\)的路径,假设该路径为\(x_i\to x_t\to\bar{x_j}\),因为建边时的对称性,就必然存在\(x_j\to\bar{x_t},\bar{x_t}\to\bar{x_i}\),这两条路径。反过来同理。
那么所有的SCC也是两两对称或者说匹配的(如果一个SCC包含若干变量的值,那么必然有另一个SCC包含这些变量的取反值)。这样我们每确定一个变量的取值,就相当于确定了该变量所在SCC中所有变量的取值并且不发生冲突。
我们来看一种发生冲突的情况来加深理解。
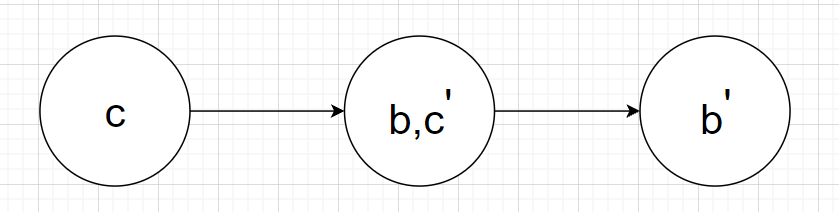
这种情况虽然满足有解的条件但是不存在解是因为\(b,\bar{c}\)在同一个SCC中,但\(c,\bar{b}\)不在同一个SCC中。
例题:P4782 【模板】2-SAT 问题
参考代码
#include<bits/stdc++.h>
using namespace std;
const int N=2*(1e6+10);
vector<int>g[N];
int n,m;
int dfn[N],low[N],scc[N],sccnt,dfcnt;
stack<int>st;
void tarjan(int u){
dfn[u]=low[u]=++dfcnt;
st.push(u);
int len=g[u].size();
for(int i=0;i<len;++i){
int v=g[u][i];
if(!dfn[v])tarjan(v),low[u]=min(low[u],low[v]);
else if(!scc[v])low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]){
++sccnt;int now;
do{
now=st.top();
st.pop();
scc[now]=sccnt;
}while(now!=u);
}
}
void fail(){
printf("IMPOSSIBLE");
exit(0);
}
int main(){
scanf("%d%d",&n,&m);
int a,b,va,vb;
for(int i=1;i<=m;++i){
scanf("%d%d%d%d",&a,&va,&b,&vb);
g[a+n*(va&1)].push_back(b+n*(vb^1));
g[b+n*(vb&1)].push_back(a+n*(va^1));
}
for(int i=1;i<=2*n;++i)if(!dfn[i])tarjan(i);
for(int i=1;i<=n;++i)if(scc[i]==scc[i+n])fail();
printf("POSSIBLE\n");
for(int i=1;i<=n;++i)printf("%d ",scc[i]<scc[i+n]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号