双连通分量
点双连通分量(bcc)
在一个连通图中(无向图)任选两点,如果他们之间至少存在两条“点不重复”的路径,称这个图为点双连通。一个图中的点双连通极大子图称为“点双连通分量”(block,2-connected component,BCC)。点双连通分量是个“可靠”的图,去掉任意一个点,其他点任然是连通的。也就是说,点双连通分量中没有[割点]。(https://www.cnblogs.com/hetailang/p/16299244.html)。
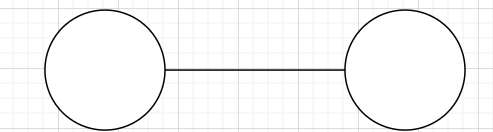
这是一种特殊的点双连通分量,因为他不满足至少两条“点不重复”的路径。
事实上除了孤立顶点外,上面那张图是最小的bcc
显然bcc中不一定有环
求解点双连通分量和求割点密切相关。不同点双连通分量最多只有一个公共点,这个点就是割点;任意一个割点都是至少两个点双连通分量的公共点。
从任意一个点开始DFS,将图中的边入栈(因为一条边属于一个BCC,而点如割点,属于多个BCC),每次确认一个点是割点,就相当于找到了个BCC。
例题:hdu 3394
参考代码
//-------------------------------
//hdu 3394
//-------------------------------
#include<iostream>
#include<stack>
#include<vector>
#include<cstring>
#include<string>
#include<cmath>
using namespace std;
const int N=1e4+10;
int n,m;
vector<int>g[N];
int low[N],dfn[N],cnt;
int bcc[N];
int bcccnt;
struct edge{
int u,v;
};
int Min(int a,int b){
return a<b?a:b;
}
stack<edge>st;
int ansa,ansb;
int tarjan(int u,int fr){
int len=g[u].size();
int lowu=low[u]=dfn[u]=++cnt;
for(int i=0;i<len;++i){
int v=g[u][i];
if(v==fr)continue;
if(!dfn[v]){
st.push({u,v});//这里要将边入栈
tarjan(v,u);
low[u]=Min(low[u],low[v]);
if(low[v]>=dfn[u]){//找到割点,u
int cnte=0,cntv=0;
if(low[v]>dfn[u])++ansa;//找到割边,uv
//不能写成low[v]>low[u]
++bcccnt;//用这个来标记点双连通分量,用cnt标记是错的
while(1){
edge e=st.top();
st.pop();
int a=e.u,b=e.v;
bcc[a]=bcccnt;
bcc[b]=bcccnt;
++cnte;
if(a==u&&b==v)break;
}
for(int i=0;i<n;++i)
if(bcc[i]==bcccnt)++cntv;
if(cnte>cntv)ansb+=cnte;
}
}
else if(dfn[u]>dfn[v])//这里是为了边的方向是返祖边,判割点可以不要这个条件,但求bcc必须加这个
low[u]=Min(low[u],dfn[v]),st.push({u,v});
}
return lowu;
}
int main(){
while(1){
scanf("%d%d",&n,&m);
if(n==0&&m==0)break;
for(int i=0;i<n;++i){
g[i].clear();
}
memset(low,0,sizeof(low));
memset(dfn,0,sizeof(dfn));
memset(bcc,0,sizeof(bcc));
ansa=ansb=0;
cnt=bcccnt=0;
int u,v;
for(int i=1;i<=m;++i){
scanf("%d%d",&u,&v);
g[u].push_back(v);
g[v].push_back(u);
}
for(int i=0;i<n;++i){
if(!dfn[i])tarjan(i,-1);
}
printf("%d %d\n",ansa,ansb);
}
}
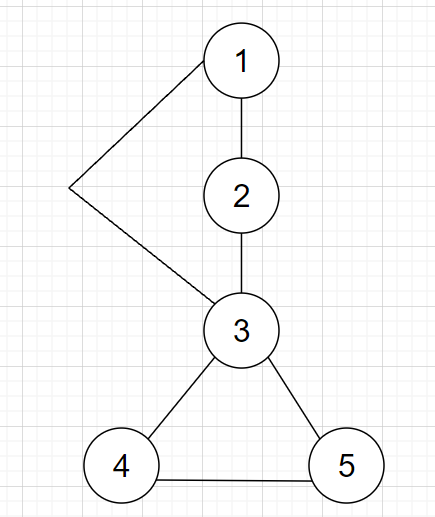
上图的3,4,5显然是个bcc,但如果不加else if(dfn[u]>dfn[v])中的判断条件,3,4,5相关的边出栈后又会将3->5这条边入栈,从而导致WA。
P8435 【模板】点双连通分量
参考代码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
const int M=2e6+10;
#define x first
#define y second
#define gt getchar()
struct{
int to,next;
}e[2*M];
int head[N],cnt;
int bcc[N],bccnt;
int dfn[N],dfcnt;
inline void add(int u,int v){
e[++cnt].next=head[u];
e[cnt].to=v;
head[u]=cnt;
}
template<typename T>
void rd(T &x){
x=0;
char ch=gt;
T f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=gt;}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=gt;}
x=x*f;
}
vector<int>ans[N];
stack<pair<int,int>>st;
int dfs(int u,int f){
int lowu=dfn[u]=++dfcnt;
if(u==f&&head[u]==0){//只有一个点也算一个bcc
bcc[u]=++bccnt;
ans[bccnt].push_back(u);
return 0;
}
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v==f)continue;
if(!dfn[v]){
st.push({u,v});
int lowv=dfs(v,u);
lowu=min(lowu,lowv);
if(lowv>=dfn[u]){
++bccnt;
while(1){
int a=st.top().x;
int b=st.top().y;
st.pop();
if(bcc[a]!=bccnt){bcc[a]=bccnt;ans[bccnt].push_back(a);}
if(bcc[b]!=bccnt){bcc[b]=bccnt;ans[bccnt].push_back(b);}
if(a==u&&b==v)break;
}
}
}
else if(dfn[v]<dfn[u]){
st.push({u,v});
lowu=min(lowu,dfn[v]);
}
}
return lowu;
}
int main(){
int n,m;
//scanf("%d%d",&n,&m);
rd(n);rd(m);
int u,v;
for(int i=1;i<=m;++i){
//scanf("%d%d",&u,&v);
rd(u);rd(v);
add(u,v);add(v,u);
}
for(int i=1;i<=n;++i){
if(!dfn[i])dfs(i,i);
}
printf("%d\n",bccnt);
for(int i=1;i<=bccnt;++i){
printf("%d ",ans[i].size());
for(auto j:ans[i]){
printf("%d ",j);
}
putchar('\n');
}
return 0;
}
边双连通分量(e-Dcc edge double connected component)
与点双连通分量类似,如果任意两点之间至少存在两条“边不重复”的路径,称为“边双连通”。在边双连通图中去掉任意一条边,图仍然是连通的。也就是说,边双连通分量没有割边。
P8436 【模板】边双连通分量
只需要把割边标记出来,剩下的就是边连通分量了。
参考代码
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
const int M=2e6+10;
int n,m;
int dcc[N],dccnt;
int head[N],cnt=1;
int dfn[N],dfcnt;
struct{
int to,next;
bool is;
}e[2*M];
inline void add(int u,int v){
e[++cnt].to=v;
e[cnt].next=head[u];
head[u]=cnt;
}
int tarjan(int u,int f){
int lowu=dfn[u]=++dfcnt;
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v==f)continue;
if(!dfn[v]){
int lowv=tarjan(v,u);
lowu=min(lowu,lowv);
if(lowv>dfn[u])e[i].is=e[i^1].is=1;//标记割边
}
else if(dfn[v]<dfn[u])lowu=min(lowu,dfn[v]);
}
return lowu;
}
vector<int>ans[N];
void dfs(int u,int v){
dcc[u]=dccnt;
ans[dccnt].push_back(u);
for(int i=head[u];i;i=e[i].next){
if(e[i].is||dcc[e[i].to])continue;
dfs(e[i].to,u);
}
return ;
}
int main(){
scanf("%d%d",&n,&m);
int u,v;
for(int i=1;i<=m;++i){
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
for(int i=1;i<=n;++i){
if(!dfn[i])tarjan(i,i);//用tarjan找dcc
}
for(int i=1;i<=n;++i){
if(!dcc[i]){
++dccnt;
dfs(i,i);//标记dcc
}
}
printf("%d\n",dccnt);
for(int i=1;i<=dccnt;++i){
printf("%d ",ans[i].size());
for(auto j:ans[i])printf("%d ",j);
putchar('\n');
}
return 0;
}
二者的关系
他们的关系其实也就是割点与割边的关系。
总的来说,点双连通分量更为严格。
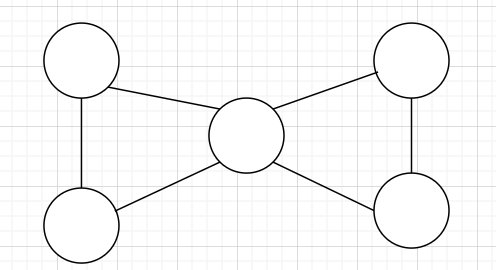
有割点无割边
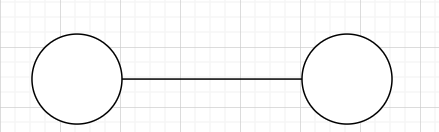
有割边无割点


 浙公网安备 33010602011771号
浙公网安备 33010602011771号