最短路常用算法
弗洛伊德(Floyd-Warshall)
时间复杂度\(O(n^3)\)
多元最短路,核心思想是依次将所有点作为中转点并更新所有路径。
核心代码也只有5行
for(int i=1;i<=n;++i)//外层循环一定是中转点
for(int j=1;j<=n;++j)
for(int k=1;k<=n;++k)
if(g[j][k]>g[j][i]+g[i][k])
g[j][k]=g[j][i]+g[i][k];
该算法也可以用来判负环,若有g[i][i]<0则存在负环。
迪杰斯特拉(dijkstra)
单源最短路,基于贪心的思想求得每个点到原点的最短距离。
注意路径不能为负。
每次选择一个离原点最近的点,那么这个点离原点的最短距离也就确定了,然后更新所有与这个点相邻点的距离。
例题:P3371 【模板】单源最短路径(弱化版)
参考代码
#include<bits/stdc++.h>
using namespace std;
int n,m,s;
const int N=1e4+10;
const int M=5e5+10;
int dis[N];
struct {
int to,next,w;
}e[M];
int head[N],cnt;
void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].w=w;
e[cnt].next=head[u];
head[u]=cnt;
}
struct node{
int d,id;
const bool operator<(const node a)const{
return d>a.d;
}
node(){}
node(int a,int b):d(a),id(b){}
};
bool vis[N];
void djk(int s){
dis[s]=0;
for(int i=1;i<=n;++i){
int ind,Min=1e9;
for(int j=1;j<=n;++j){//找到离原点最近的点
if(!vis[j]&&dis[j]<Min){
ind=j;
Min=dis[j];
}
}
vis[ind]=1;
for(int j=head[ind];j;j=e[j].next){//更新
int to=e[j].to;
dis[to]=min(dis[to],dis[ind]+e[j].w);
}
}
}
int main(){
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<=n;++i)dis[i]=INT_MAX;
int u,v,w;
for(int i=1;i<=m;++i){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
}
djk(s);
for(int i=1;i<=n;++i)printf("%d ",dis[i]);
return 0;
}
该算法是djk朴素算法,时间复杂度为\(O(n^2)\)
djk堆优化(劣化)
如果使用堆来解决找离原点最近的点,那么这部分的时间复杂度变为\(O(logN)\),总的时间复杂度是\(O((M+N)logN)\)
最坏情况下\(M=N^2\),堆优化就变成了堆劣化。
参考代码
#include<bits/stdc++.h>
using namespace std;
int n,m,s;
const int N=1e4+10;
const int M=5e5+10;
int dis[N];
struct {
int to,next,w;
}e[M];
int head[N],cnt;
void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].w=w;
e[cnt].next=head[u];
head[u]=cnt;
}
struct node{
int d,id;
const bool operator<(const node a)const{
return d>a.d;
}
node(){}
node(int a,int b):d(a),id(b){}
};
priority_queue<node>q;
bool vis[N];
void djk(int s){
dis[s]=0;
q.push(node(0,s));
node now;
while(q.size()){
now=q.top();//这里的复杂度为NlogN
q.pop();
int id=now.id,to;
if(vis[id])continue;//找到最短路的点直接跳过
vis[id]=1;
for(int i=head[id];i;i=e[i].next){
to=e[i].to;
if(dis[to]>dis[id]+e[i].w){//这里的复杂度为MlogN
dis[to]=dis[id]+e[i].w;
q.push(node(dis[to],to));
}
}
}
}
int main(){
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<=n;++i)dis[i]=INT_MAX;
int u,v,w;
for(int i=1;i<=m;++i){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
}
djk(s);
for(int i=1;i<=n;++i)printf("%d ",dis[i]);
return 0;
}
贝尔曼-福特(Bellman-Ford)
单源最短路,这种算法可以解决带负权边的图(也可以判断图中是否有负环)。
基本思路与弗洛伊德有点像,不断地向图中加入中转边。
看一张图
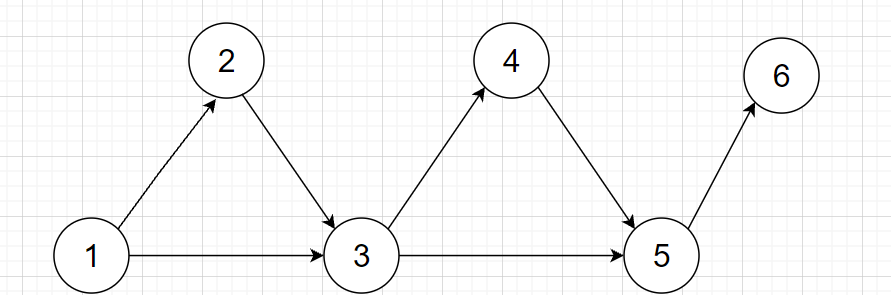
只看其中的一条路径

如果加边的方向刚好是从左到右,那么很快就能得到1->6的最短路,
如果方向相反,把所有边加入依次只能得到1->2的最短路。
为了解决加边随机性的问题,我们需要重复加边。
核心代码
for(int k=1;k<=n-1;++k)
for(int i=1;i<=m;++i)//一次加入(松弛)所有边,由于顺序可能不是最优的,所以这个过程要重复n-1次,循环i次,就可以得到长度为i的最短路
if(dis[v[i]]>dis[u[i]]+w[i])
dis[v[i]]=dis[u[i]]+w[i];
检查负权回路只需多松弛一次,若还能更新最短路,则有负权回路
时间复杂度\(O(MN)\)
Bellman-Ford的队列优化
在每一次松弛后,有一些点已经求得了最短距离,它们不再受接下来松弛的影响。
这就启发我们只对最短距离发生变化的点的出边进行松弛。
整个过程用队列来维护即可。
例题:P3371 【模板】单源最短路径(弱化版)
参考代码
#include<bits/stdc++.h>
using namespace std;
int n,m,s;
const int N=1e4+10;
const int M=5e5+10;
int dis[N];
struct {
int to,next,w;
}e[M];
int head[N],cnt;
void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].w=w;
e[cnt].next=head[u];
head[u]=cnt;
}
struct node{
int d,id;
const bool operator<(const node a)const{
return d>a.d;
}
node(){}
node(int a,int b):d(a),id(b){}
};
queue<node>q;
bool vis[N];
void spfa(int s){
dis[s]=0;
q.push(node(0,s));
node now;
while(q.size()){ //这里跟bfs很像,从小到大寻找长度从1到n-1的最短路
now=q.front();
q.pop();
int id=now.id,to;
vis[id]=0;
for(int i=head[id];i;i=e[i].next){
to=e[i].to;
if(dis[to]>dis[id]+e[i].w){
dis[to]=dis[id]+e[i].w;
if(!vis[to])q.push(node(dis[to],to)),vis[to]=1;//一个点重复入队没有意义
}
}
}
}
int main(){
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<=n;++i)dis[i]=INT_MAX;
int u,v,w;
for(int i=1;i<=m;++i){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
}
spfa(s);
for(int i=1;i<=n;++i)printf("%d ",dis[i]);
return 0;
}
然而它最坏复杂度也为\(O(MN)\)
如果一个点入队超过n次,那么存在负环。
关于这里到底入队多少次才能判断,有一位大佬跟我说过,spfa本质是bellman-ford,
bellman-ford松弛n-1次,那么这里入队n次就能判断。
总结
| Floyd | Dijkstra | Bellman-Ford | spfa | |
|---|---|---|---|---|
| 时间复杂度 | \(O(N^3)\) | \(O((M+N)logN)\)或者\(O(N^2)\) | \(O(MN)\) | \(O(MN)\) |
| 是否可处理负权边 | 可以 | 不可以 | 可以 | 可以 |
| 是否可判断负权环 | 可以 | 不能 | 可以 | 可以 |
DAG(Directed Acyclic Graph,有向无环图)最短(长)路
当一张图为有向无环图时,可以根据节点拓扑序列,用DP快速求解。
例题:Test for Job
参考代码
注意多组数据清空
#include <iostream>
#include <queue>
#include <algorithm>
#include <string.h>
using namespace std;
const int N = 1e5 + 10;
const int M = 1e6 + 10;
int topo[N], p[N], ind[N], cnt_t, out[N];
int head[N], cnt;
struct
{
int v, next;
}e[M];
int n, m;
void add(int u, int v)
{
e[++cnt].v = v;
e[cnt].next = head[u];
head[u] = cnt;
}
void get_topo()
{
queue<int> q;
for (int i = 1; i <= n; ++i)
{
if (ind[i] == 0)
q.push(i);
}
while (q.size())
{
int u = q.front();
q.pop();
topo[cnt_t++] = u;
int v;
for (int i = head[u]; i; i = e[i].next)
{
v = e[i].v;
--ind[v];
if (ind[v] == 0)
q.push(v);
}
}
}
int ans[N], mark[N];
int answ = -2e9;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
while (cin >> n >> m)
{
memset(head, 0, sizeof(head));
memset(ans, 0, sizeof(ans));
memset(mark, 0, sizeof(mark));
cnt = 0;
cnt_t = 0;
answ = -2e9;
for (int i = 1; i <= n; ++i)
cin >> p[i];
int u, v;
for (int i = 0; i < m; ++i)
{
cin >> u >> v;
++ind[v];
++out[u];
add(u, v);
}
get_topo();
for (int i = 0; i < n; ++i)
{
//cout << topo[i] << " ";
int u = topo[i];
ans[u] += p[u];
if (out[u] == 0)
answ = max(answ, ans[u]);
out[u] = 0;
for (int j = head[u]; j; j = e[j].next)
{
v = e[j].v;
if (!mark[v])
{
ans[v] = ans[u];
mark[v] = 1;
}
else
ans[v] = max(ans[v], ans[u]);
}
}
cout << answ << endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号