割点和割边

定义

在无向图中，所有能互通的点组成了一个“连通分量”。在一个连通分量中有一些关键的点，如果删除它们，会把这个连通分量分成两个或更多，这种点称为割点(Cut vertex)。
类似的有割边(Cut edge，又称为桥，bridge)问题。在一个连通分量中，如果删除一条边，把这个连通两个(注意边最多只能分成两个)，则这个边称为割边。

用DFS求割点

在一个连通分量G中，对任意一个点s左DFS。能访问到所有点，产生一颗“深度优先生成树”。那么对G求割点，和T有什么关系呢？

定理1
T的根节点时割点，当且仅当s有两个或更多个子结点。

这个很好理解，如果s是割点，那么它会把图分成几个不相连的部分，这几个部分对应着T中的不同子树。

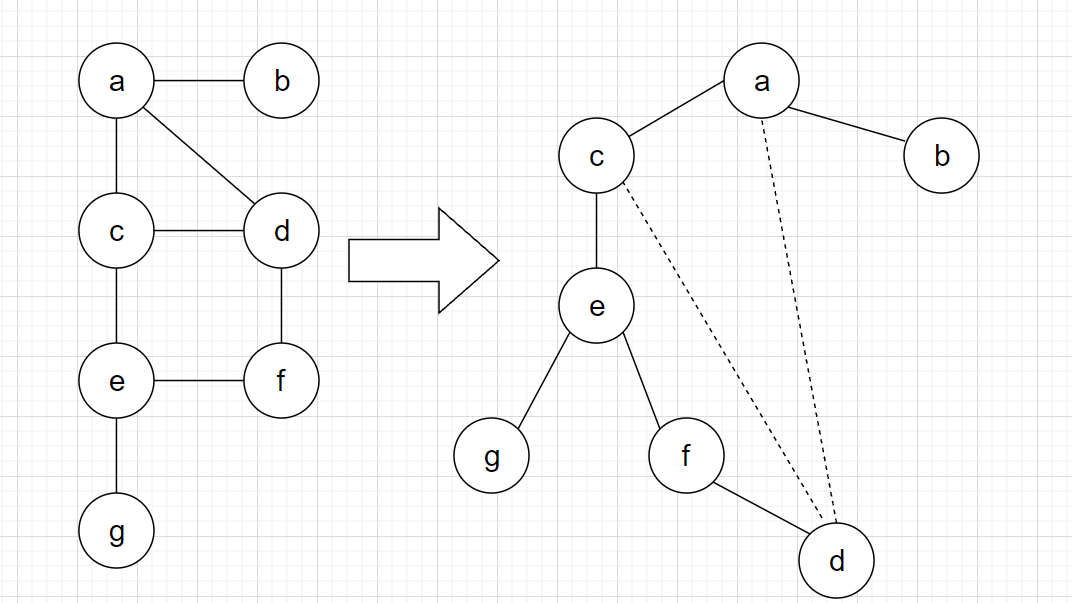
在这个图中可以很方便的验证这个定理。

定理2
T的非根结点u是割点，当且仅当u存在一个子结点v，v及其后代都没有回退边连回u的祖先(返祖边，右图中的虚线)。

这就是说，如果非根结点u是割点，那么它最起码会把图分为上下两个部分，上面是祖先，下面是后代，并且这两部分不能相连。
例如上图的c不是割点而e是割点(它的子结点g及其后代没有产生返祖边)。

注意根节点与非根结点的判断方法不同。

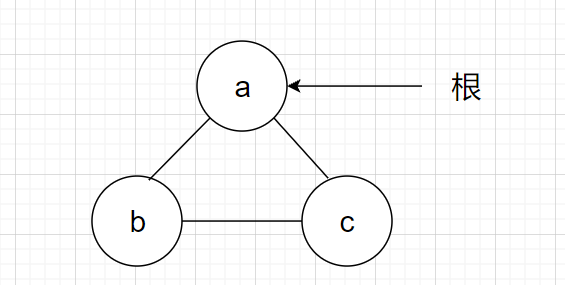
上面那个图，若按非根结点判断则a是割点，但实际上它不是割点。

代码实现

关键就在于如何判断一个结点是否能访问到某个结点的祖先。
定义dfn[i]表示i点的时间戳，就是i点是第几个被访问到的。
定义low[i]表示i点及其后代能连接(这里连接的意思是不能无限制的向上找祖先，参考下面的图和代码)到的最早祖先。
现在设u的一个子结点是v。
如果有low[v]>=dfn[u]，就说明通过v回不到u的祖先了。

例题
P3388 【模板】割点（割顶）
参考代码

#include<bits/stdc++.h>
using namespace std;
const int N=2e4+10;
const int M=1e5+10;
struct{
	int to,next;
}e[2*M];
int n,m;
int head[N],cnt;
int dfn[N],low[N];
bool is[N];
void add(int a,int b){
	e[++cnt].to=b;
	e[cnt].next=head[a];
	head[a]=cnt;
}
int cdfn=0;
int tot;
void dfs(int x,int fr){
	int child=0;
	dfn[x]=low[x]=++cdfn;//默认两者相同
	for(int i=head[x];i;i=e[i].next){
		int to=e[i].to;
		if(to==fr)continue;//下一个结点是父节点直接跳过，子结点当然不包括父节点
		if(!dfn[to]){//如果下个点没有访问过
		++child;     //得到一棵子树
		dfs(to,x);
		low[x]=min(low[x],low[to]);  //直接用子结点的low更新当前结点的low
		if(x!=fr&&low[to]>=dfn[x])is[x]=1;//只有当to是x的后代时才能判断割点
		}
	else if(dfn[to]<dfn[x])low[x]=min(low[x],dfn[to]);//是当前结点的祖先，直接更新low
        //这里不能写成low[x]=min(low[x],low[to]),参考下面的图
	}	
	if(x==fr&&child>=2)is[x]=1;//判断根节点是否是割点
}
int main(){
	scanf("%d%d",&n,&m);
	int a,b;
	for(int i=1;i<=m;++i){
		scanf("%d%d",&a,&b);
		add(a,b);
		add(b,a);
	}
	for(int i=1;i<=n;++i){
		if(!dfn[i])dfs(i,i);
	}
	for(int i=1;i<=n;++i)if(is[i])++tot;
	printf("%d\n",tot);
	for(int i=1;i<=n;++i){
		if(is[i])printf("%d ",i);
	}
	return 0;
}

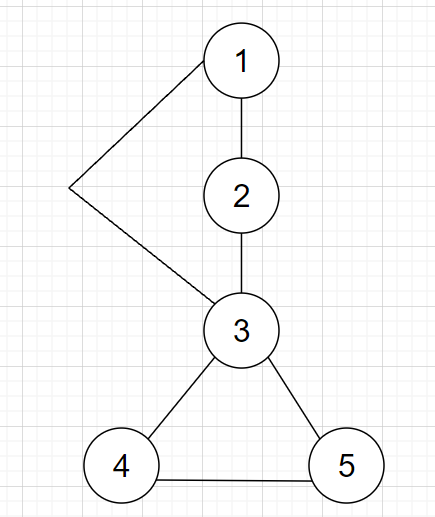
显然3号点是割点，但是else if(dfn[to]<dfn[x])low[x]=min(low[x],low[to]);low[5]=1，进而无法判断3号点为割点。

割边

只要将low[v]>=dfn[u]改成low[v]>dfn[u]即可判断割边，因为v及其子结点若能到达u，显然删除u->v这条边不能断开他们。

二者的关系

他们的关系其实也就是割点与割边的关系。
总的来说，点双连通分量更为严格。

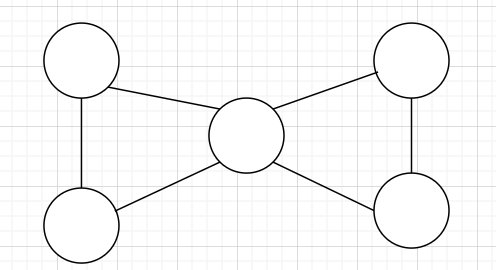
有割点无割边

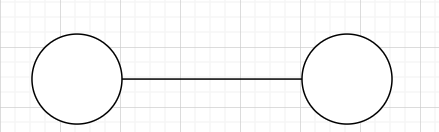
有割边无割点