欧拉路径(回路)

定义

欧拉路径
图中所有的边都经过且只经过一次(一笔画)。
欧拉回路
起点与终点相同的欧拉路径。

欧拉路径(回路)判定

有向图的欧拉路径
图中恰好存在一个点出度比入度多一(起点)，一个点入度比出度多一(终点)，其余节点出度=入度(可进可出)。

有向图的欧拉回路
所有点的入度=出度(任意点可作为起点和终点)。

无向图的欧拉路径
图中恰好存在两个度数为奇数的点(作为起点和终点)，其余节点的度数为偶数。

无向图的欧拉回路
图中所有点的度数为偶数。

容易发现一个图中若存在欧拉回路，那么一定存在欧拉路径。

寻找欧拉路径(默认已经存在欧拉路径)

首先我们可以发现，如果我们直接dfs，可能得不到我们想要的欧拉路径。

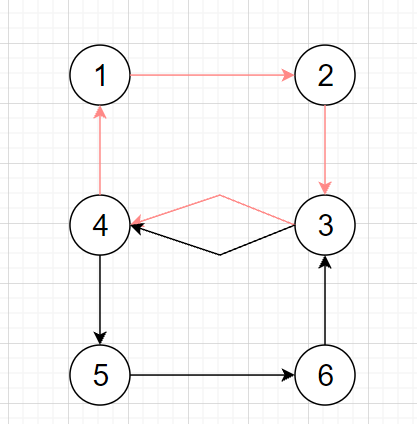
从1号点开始出发，1->2->3->4->1。又回到了1号结点，但没有走完所有路径。
从“一笔画”这个游戏中我们可以发现，我们不能保证我们连接的路径一定是对的，对于上述那种情况，
我们应该退回到4号结点，走其他路径。
那在计算机中怎么表示这种“回退”呢？
当我们错误的从4号点走到1号点，到达1号点发现无路可走，但仍有边没有走到，
也就是说，我们过早的走到1号点，正确的的路径应该是这样1->2->3->4->.....->1。
这个时候我们就可以确定4->1(也就是1号点)应该在最后面(这是个必要条件)，那么我们就确定了路径的最后一个点。
通过上面的分析可以发现，当到达一个点无路可走时，它在欧拉路径中的位置也就确定了(我称之为反向确定路径法)。

例题
P7771 【模板】欧拉路径

参考代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
const int M=2e5+10;
int rd[N],cd[N];
vector<int>g[N];
int n,m,dfn[N];
stack<int>st;
void dfs(int x){
	int len=g[x].size();
	for(int i=dfn[x];i<len;i=dfn[x]){
		++dfn[x];//图中是存在环的，这个东西用来防止重复走同一条边
		dfs(g[x][i]);
	}
        //此时已无路可走，记录路径
	st.push(x);
}
int main(){
	scanf("%d%d",&n,&m);
	int u,v;
	for(int i=1;i<=m;++i){
		scanf("%d%d",&u,&v);
		g[u].push_back(v);
		++rd[v],++cd[u];
	}
	bool f=1;
	int s=1,cnt1=0,cnt2=0;
	for(int i=1;i<=n;++i){
		if(rd[i]!=cd[i])f=0;
		if(rd[i]+1==cd[i])++cnt1,s=i;
		if(cd[i]+1==rd[i])++cnt2;
	}
	if(!f&&!(cnt1==cnt2&&cnt1==1)){
		printf("No\n");
		return 0;
	}
	for(int i=1;i<=n;++i)sort(g[i].begin(),g[i].end());
	dfs(s);
	while(st.size()){
		printf("%d ",st.top()),st.pop();
	}
	return 0;
}