拓扑排序

一个图能进行拓扑排序的充要条件是它是一个有向无环图(DAG directed acyclic graph)。

基于BFS的拓扑排序

先将所有入度为0的点放入队列中(顺序无关紧要)，每次将队首弹出的点加入拓扑序列中，然后将该点所有的相邻点入度减1，将入度减为0的点入队。
当队列为空时，若所有点都以加入拓扑序列，则完成退出，反之该图不存在拓扑序列。
参考代码

void topo(){
    for(int i=1;i<=n;++i){
        if(ind[i]==0){q.push(i);
        ts[++tot]=i;}
    }
    int now,next;
    while(!q.empty()){
        now=q.front();
        q.pop();
        for(int i=0;i<node[now].size();++i){
            next=node[now][i];
            if(--ind[next]==0){
                q.push(next);
                ts[++tot]=next;
            }
        }
    }

基于DFS的拓扑排序

DFS沿着一条路径走到底，然后逐层退回，这个过程体现了点与点之间的先后关系，天然符合拓扑排序的原理。

一条有向边A->B，表示A的拓扑序必定在B之前。就是说从一个点出发，所有可以到达的点的拓扑序都在该点之后。如果一个点的出度为0或者它的所有出边都访问完了，那么现在在所有未访问完的的点中，已经没有拓扑序比该点还大的点了，所以该点的拓扑序可以确定。故我们可以在dfs中访问完该点的所有出边后确定该点的拓扑序。

首先在一个图中使用dfs会产生一个深搜优先生成树。

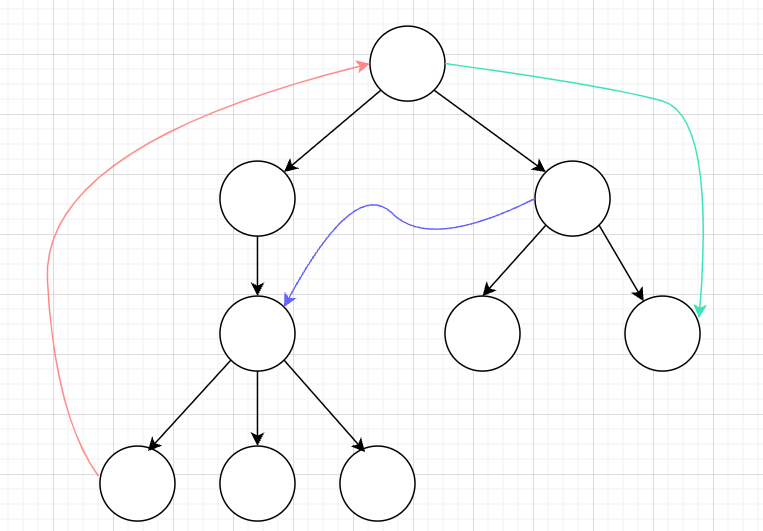
黑色的边叫树边，这些边构成了深搜优先生成树。
红色的边叫返祖边，这些边指向祖先。
绿色的边叫前向边，这些边指向孙子，孙孙子。。。(注意不包括儿子)。
蓝色的边叫横插边，这些边上的两个节点没有子孙关系(相对于深搜优先生成树来讲)。
显然一个图中只有不产生返祖边才能有拓扑排序。

bool dfs(int s){
	vis[s]=-1;
	int next;
	for(int i=0;i<node[s].size();++i){
		next=node[s][i];
		if(vis[next]<0)return false;//发现返祖边,-1是为了区分子孙与祖先 
		if(vis[next]==0&&!dfs(next))return false; 
	}
	vis[s]=1;
	ts[tot--]=s;//加入拓扑排序
	return true; 
}
bool topo(){
	tot=n;
	bool f=1;
  for(int i=1;i<=n;++i){
  	if(ind[i]==0&&vis[i]==0){
  		f=dfs(i);
  		if(f==0)return false;
  	}
  }
}