DFS序与欧拉序

DFS序

DFS序代表着树从根节点开始进行DFS的节点的遍历顺序。

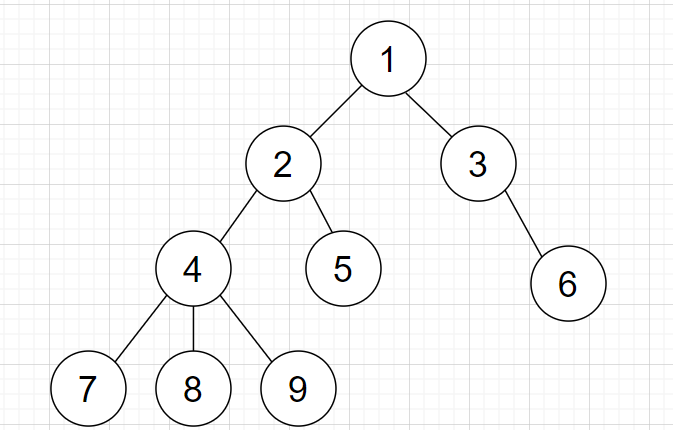
那么上图的DFS序显然为1，2，4，7，8，9，5，3，6
容易发现一棵子树内所有结点的DFS序是连续的，并且根节点的DFS序最小。那么假设我们已经有整颗树的DFS序为dfn[u]，
子树的大小为size[u]，就可以得到结点u的所有子树对应的DFS序区间为[dfn[u],dfn[u]+size[u]-1]。
于是，借助DFS序，可以将一棵树转化为一维数组，对某子树进行操作时，相当于在对应的DFS序区间内进行操作。
同时，也可以快速判断一个结点是否在某子树内。
参考代码

void dfs(int s,int f){
	dfn[s]=++id;
	size[s]=1;
	int to;
	for(int i=head[s];i;i=e[i].next){
		to=e[i].to;
		if(to==f)continue;
		dfs(to,s);
		size[s]+=size[to];
	}
	return ;
}

欧拉序

欧拉序与DFS序很像，但有不同。欧拉序代表从根节点出发，按照DFS的顺序经过所有节点再返回原结点的遍历顺序(即返回时也要记录)。
欧拉序有两种。
1.DFS时，第一次到达该结点记录一次，随后每访问完该结点的一棵子树就再记录一次，一共2n-1(每有一条边就有两个结点要访问，外加根节点被多访问一次)个编号。

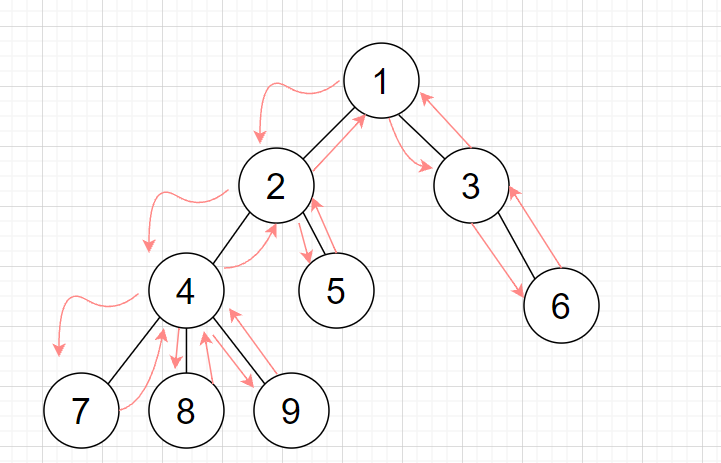
上图的欧拉序为1，2，4，7，4，8，4，9，4，2，5，2，1，3，6，3，1
参考代码

void dfs(int s,int f){
	dfn[++id]=s;//这个时候每个点可能不止出现一次，就直接记录数组了
	size[s]=1;
	int to;
	for(int i=head[s];i;i=e[i].next){
		to=e[i].to;
		if(to==f)continue;
		dfs(to,s);
                dfn[++id]=s;//在这里返回时也要记录一下
		size[s]+=size[to];
	}
	return ;
}

2.DFS时，每个节点入栈与出栈时分别记录一次，共2n个编号。

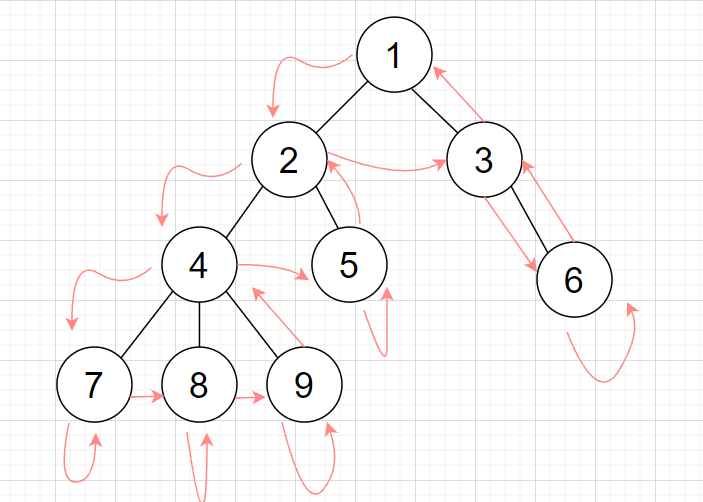
上图的欧拉序为1,2,4,7,7,8,8,9,9,4,5,5,2,3,6,6,3,1
参考代码

void dfs(int s,int f){
	dfn[++id]=s;//入栈时记录
	size[s]=1;
	int to;
	for(int i=head[s];i;i=e[i].next){
		to=e[i].to;
		if(to==f)continue;
		dfs(to,s);
		size[s]+=size[to];
	} 
        dfn[++id]=s;//出栈时记录
	return ;
}

性质

• 一结点u为根的子树包含的结点，是欧拉序区间[first[u],last[u]]之间的所有节点。换句话说就是[first[u],last[u]]之间的结点为u的子节点。
  其中first[u]是欧拉序中u第一次出现的位置，last[u]同理。

• 第一种欧拉序
  树上两点u,v的最近公共祖先，为欧拉序区间[first[u],first[v]]或[first[v],first[u]]中时间戳最小的结点，时间戳表示第一次遍历到该结点的时间。

简单证明一下：假设v，u的最近公共祖先为w，显然u，v，在w的不同子树中。那么访问完包括u或v的一棵子树后，在欧拉序中就会出现w，然后在向另一个结点遍历。
故w一定会出现在[first[u],first[v]]或[first[v],first[u]]中。

例题
祖孙询问
基本思路
直接用DFS序或欧拉序判断下祖孙关系即可。
参考代码

#include<bits/stdc++.h>
const int N=4e4+10;
int dfn[N],id,size[N];
int n,m;
struct{
	int to,next;
}e[2*N];
int head[N],cnt;
inline void add(int a,int b){
	e[++cnt].to=b;
	e[cnt].next=head[a];
	head[a]=cnt;
}
int root;
void dfs(int s,int f){
	dfn[s]=++id;
	size[s]=1;
	int to;
	for(int i=head[s];i;i=e[i].next){
		to=e[i].to;
		if(to==f)continue;
		dfs(to,s);
		size[s]+=size[to];
	}
	return ;
}
int main(){
	scanf("%d",&n);
	int a,b;
	for(int i=1;i<=n;++i){
		scanf("%d%d",&a,&b);
		if(b==-1)root=a;
		else add(a,b),add(b,a);
	}
	dfs(root,-1);
	scanf("%d",&m);
	for(int i=1;i<=m;++i){
		scanf("%d%d",&a,&b);
		if(dfn[a]<dfn[b]&&dfn[a]+size[a]-1>=dfn[b])printf("1\n");
		else if(dfn[b]<dfn[a]&&dfn[b]+size[b]-1>=dfn[a])printf("2\n");
		else printf("0\n");
	}
	return 0;
}

参考了xhp学长的ppt😁