二分图
定义
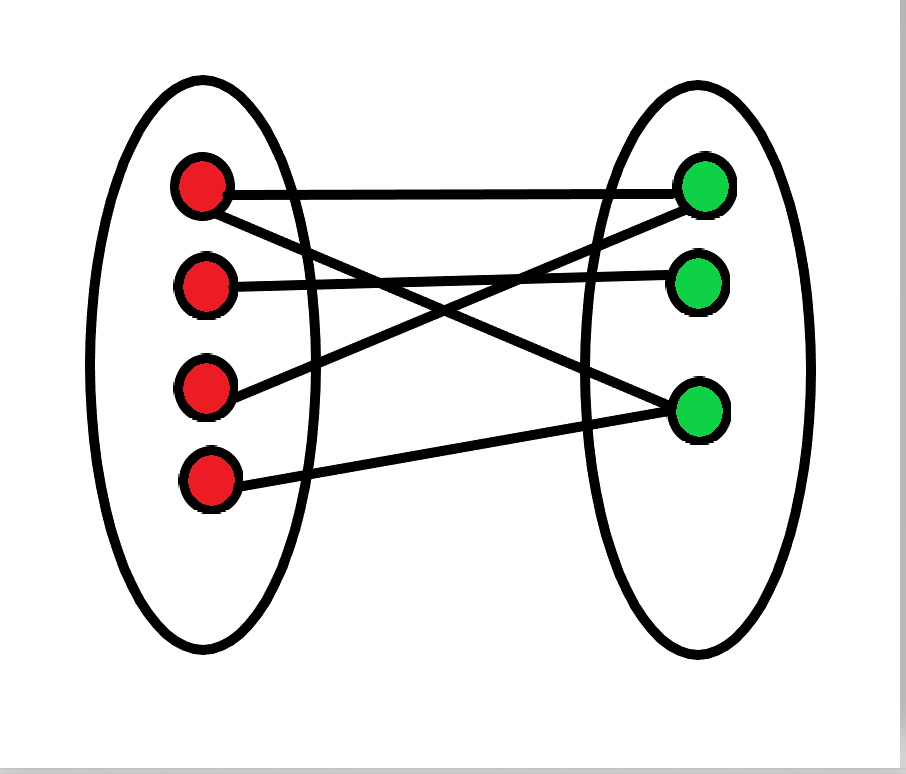
二分图又称作二部图，是图论中的一种特殊模型。设G=(V,E)是一个无向图，如果顶点V可分割为互不相交的子集(A,B)，并且图中每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集\((i\in A,j\in B)\)，则称图G为一个二分图。
就是说无向图G中所有点划分为两个集合，并且任意一条边上的两个点不能属于同一集合。
判断方法
在dfs的过程中进行染色，每条边上的两个点只能一个染0，一个染1，能满足要求即是二分图，不能则不是二分图，注意至少要有两个点。
参考代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
int f[N];
vector<int>g[N];
int n,m;//点数，边数
bool dfs(int x,int c){
f[x]=c;
int len=g[x].size(),to;
for(int i=0;i<len;++i){
to=g[x][i];
if(f[to]==c)return false;
else if(f[to]==-1) if(!dfs(to,c^1))return false;
}
return true;
}
int main(){
scanf("%d%d",&n,&m);
int a,b;
for(int i=0;i<m;++i){
scanf("%d%d",&a,&b);
g[a].push_back(b);
g[b].push_back(a);
}
//建图
if(n==1){printf("Not a bipartite graph\n");return 0;}
for(int i=1;i<=n;++i)f[i]=-1;
bool flag=0;
for(int i=1;i<=n;++i){
if(f[i]==-1&&!dfs(i,0)){flag=1;printf("Not a bipartite graph\n");break;}
}
if(!flag)printf("It's a bipartite graph\n");
return 0;
}
最大匹配
给定一个二分图G，在G的一个子图M中，M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配。选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)
如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。
简单总结一下：
1.在一个循环中依次给每个男生找对象(打个比方)。
2.依次访问每个可能成功的女生。
3.如果这名女生是在本轮循环中第一次访问到并且也还没对象，那么匹配成功。
4.如果这名女生是在本轮循环中第一次访问到但是有对象男2了，那么我们可以试着(如果失败的话就为当前男生找其他女生，男2不受影响)为男2找其他对象，这样就又来到了第一步。
5.如果这名女生是第二次访问到，那么她跟当前男生肯定是没戏了。(如果接着访问，在程序中体现为无限递归)
6.如果循环结构中的男生匹配完所有可能的女生都失败了，那么他就落单了。
例题：矩阵游戏
思路
将行与列进行匹配，若某一行与某一列的交点为1，则该行与该列之间连有边，可以发现行交换与列交换并不会改变最大匹配数(其实就是交换两个点的顺序而已，整个图的结构没有变化)，只要最大匹配数为n就有解。
参考代码
#include<bits/stdc++.h>
using namespace std;
const int N=500;
vector<int>node[N];
int t,n,a;
int match[N],used[N];
bool dfs(int x){
int to,len=node[x].size();
for(int i=0;i<len;++i){
to=node[x][i];
if(!used[to]){
used[to]=1;
if(!match[to]||dfs(match[to])){
match[to]=x;
return true;
}
}
}
return false;
}
int ans;
int main(){
scanf("%d",&t);
while(t--){
ans=0;
memset(match,0,sizeof(match));
scanf("%d",&n);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j){
scanf("%d",&a);
if(a){
node[i].push_back(j+n);
}
}
for(int i=1;i<=n;++i){
memset(used,0,sizeof(used));
if(dfs(i))++ans;
}
for(int i=1;i<=n;++i)
node[i].clear();
if(ans==n)
printf("Yes\n");
else printf("No\n");
}
return 0;
}
时间复杂度为\(O(nm)\)
