targan求强连通分量
题目简述
在一个有向图中，寻找最大的连通分量并输出(如果有两个连通分量相同输出字典序小的)。
相关知识
连通
无向图中的两个点可相互到达，则这两个点是连通的。
有向图中的两个点可相互到达，则这两个点是强连通的。
连通图
无(有)向图中，所有的点都可相互到达。
连通分量
无向图中的双连通分量(点双连通分量，边双连通分量)是个子图，该子图中任意两个点可互相到达。
有向图中称为强连通分量(Strongly Connected Component)，强连通分量是个子图，该子图中任意两个点可互相到达。
时间戳
在一次搜索过程中，第几个搜索到这个点，这个点的时间戳就为几。
相关变量
每个点有两个参数，dfn，low。
dfn表示该点的时间戳，low表示该点可以到达的所有点中最小的时间戳(其实并不是这样，后面有反例)。
思路
在dfs的过程中不断更新dfn,low这两个变量，并将访问到的点入栈(这个栈用来将不同的SCC分开，求无向图的连通分量不需要栈)。
具体操作：每到达一个点，先将该点入栈，然后尝试访问下一个点，
若下一个点没有被访问过，则dfs，
若下一个点被访问过且在当前栈里，则直接利用下一个点的dfn更新当前点的low。
dfs回溯的过程中也要更新low。
我们先看下在一个连通图中使用该算法是个什么情况。
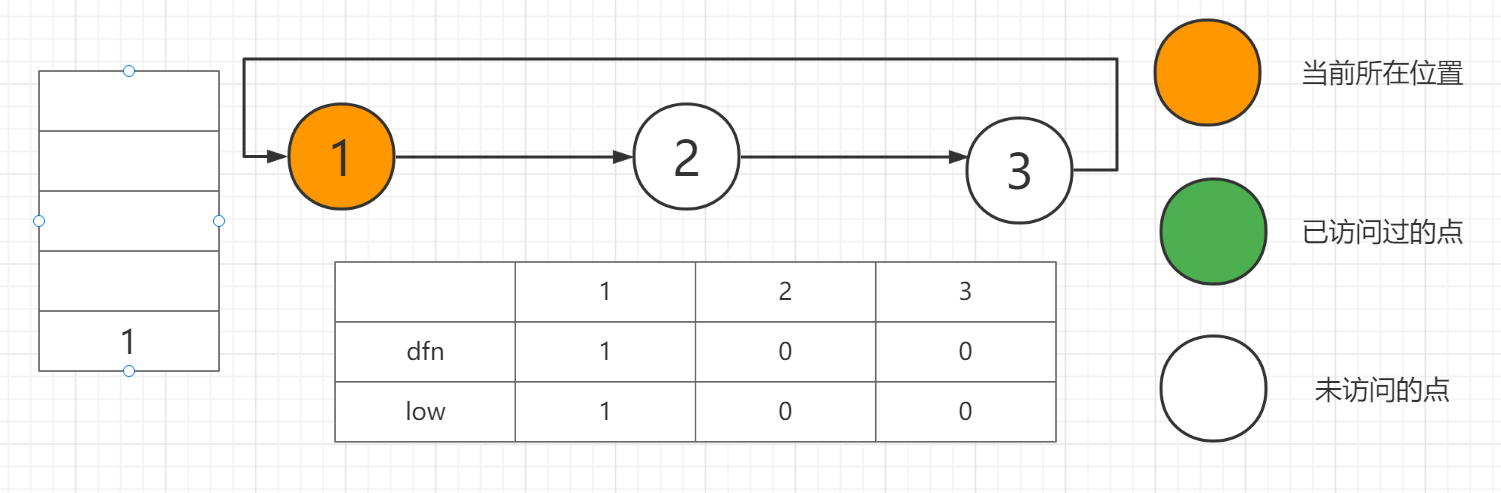
我们从1开始，先将1入栈，此时1号点的dfn，low都为1，其它点为初始值0。
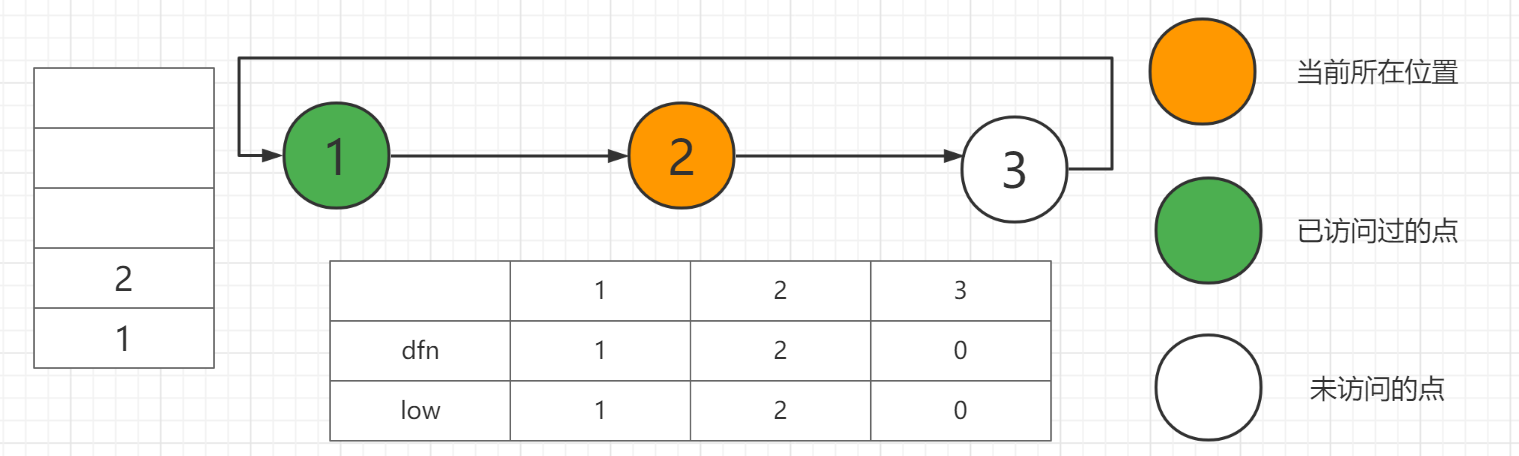
从1号点来到2号点，将2入栈并更新dfs与low。
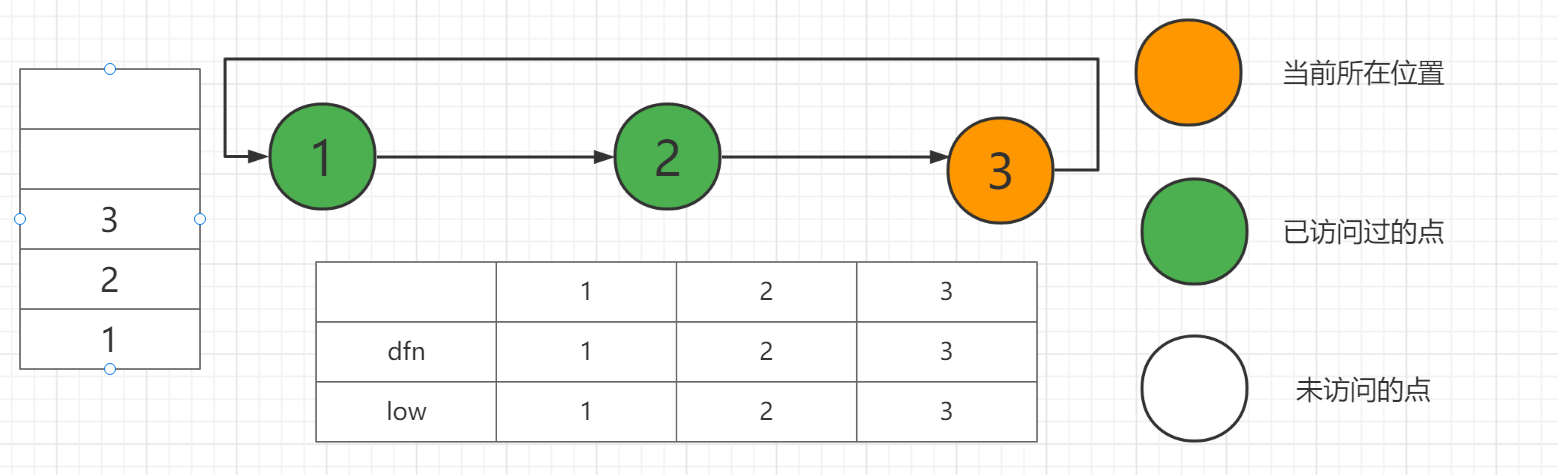
从2来到3进行相同的操作。
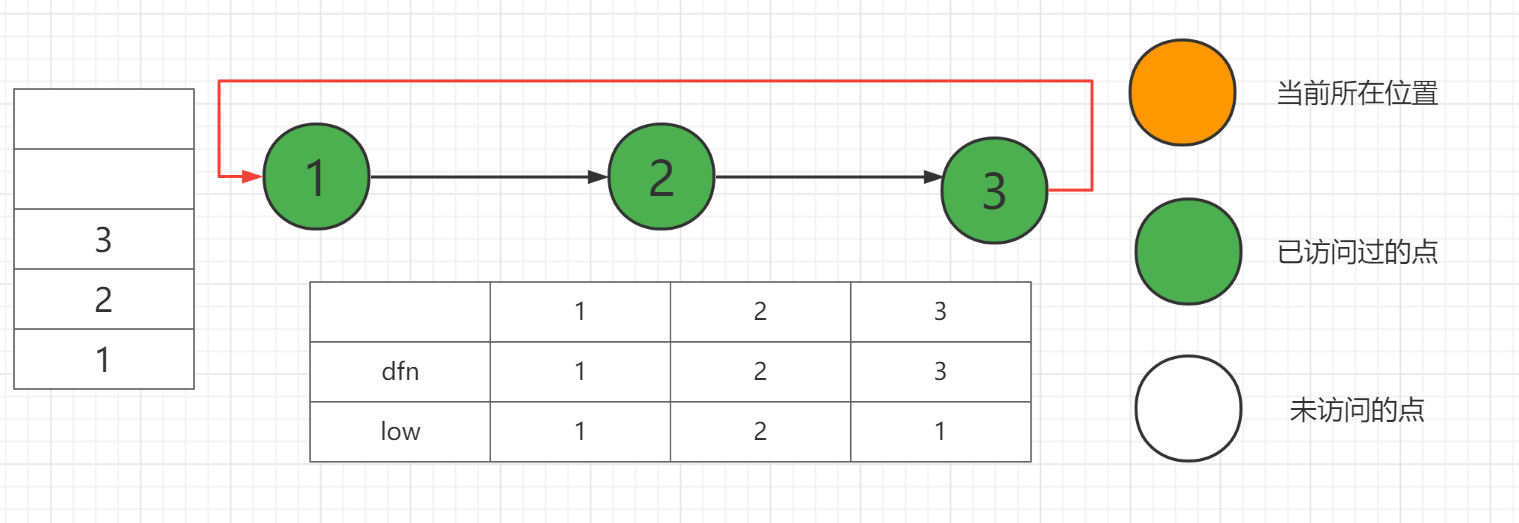
从3试图访问1就要注意了，由于1已经在栈里，故不对1dfs，直接更新3的low，然后开始回溯。
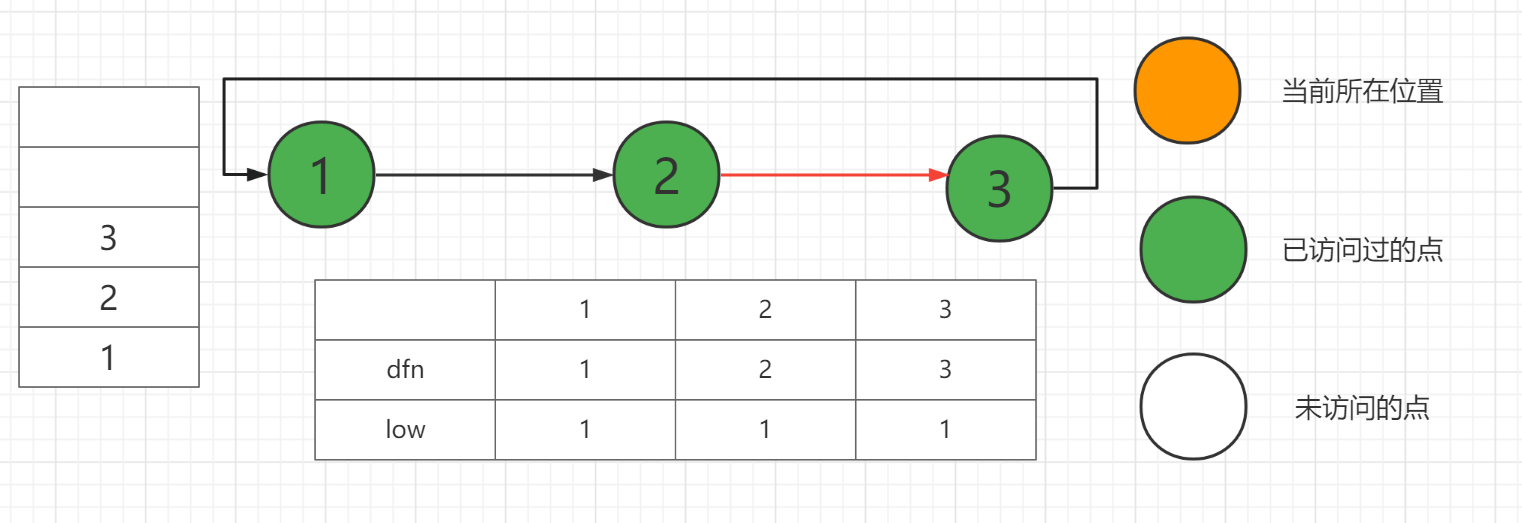
从3回到2时，用3的low更新2的low(即low[2]=min(low[2],low[3]))，这是因为3能到达的点2一定能到达。
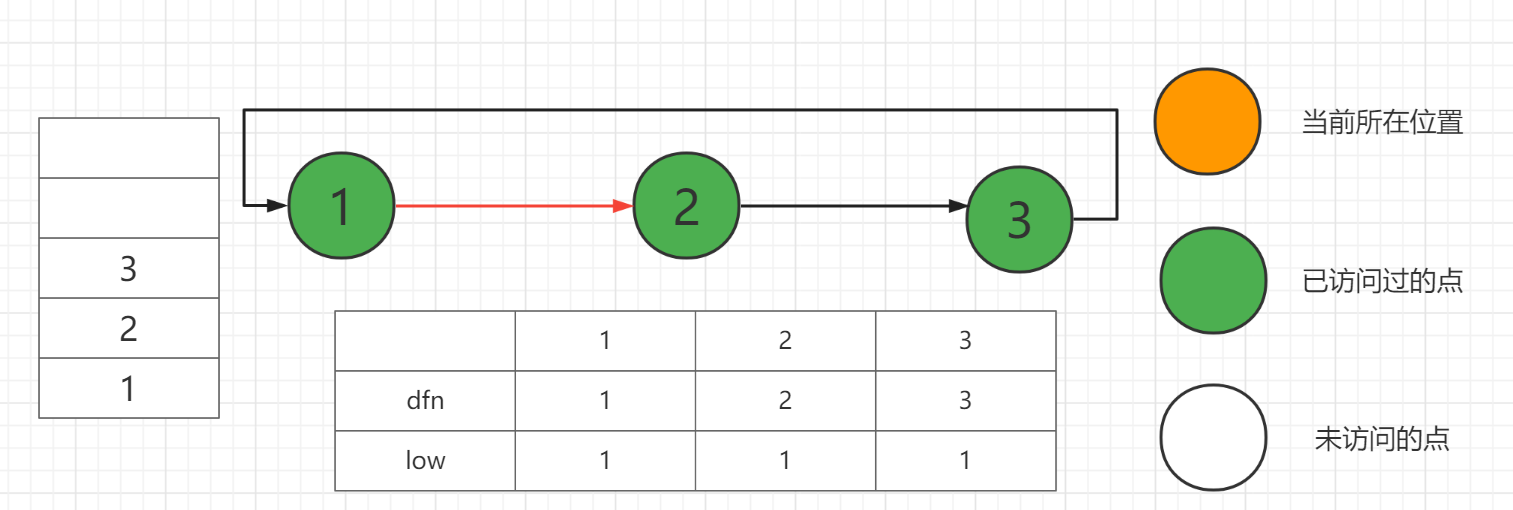
最后回到1，从1开始的dfs结束，此时有\(low[1]==dfn[1]\)，这意味着我们找到了一个连通分量1,2,3。
此时\(low[2]==low[3]==1\)。这说明2，3都能到达1，又因为这次dfs是从1开始，所以1也能到达2，3。
这就解释了为什么这些变量(dfn,low)能确定一个连通分量。
再看栈中的元素，2，3都位于1的上面，将1及以上的元素出栈即可得到对应的连通分量。
具体细节请看代码
参考代码
#include<bits/stdc++.h>
using namespace std;
const int N=5e3+10;
vector<int>g[N];//存图
int n,m;
int ans,f[N],cnt[N],Max;
//ans是连通分量的个数，f[i]表示i属于哪个连通分量，cnt[i]表示第i个连通分量的大小
//Max是最大连通分量的大小
int dfn[N],low[N],tim;
stack<int>st;//栈来存储连通分量
void targan(int x){
st.push(x);//每到一个元素先入栈
dfn[x]=low[x]=++tim;//更新dfn与low
for(int i=0;i<g[x].size();++i){
int to=g[x][i];
//注意这里就不要加if(v==f)continue;
if(!dfn[to])targan(to),
low[x]=min(low[x],low[to]);//如果to没有被访问过，就dfs，返回的时候更新low
else if(!f[to])low[x]=min(low[x],dfn[to]);//其实这里改成min(low[x],low[to])也没事，反正最终判的是low[x]==dfn[x]
//如果to在当前的栈里面，说明to已经是x的祖先(从x可以到to)，直接更新low
//这里直接用f判断是否在栈里面了
}
if(low[x]==dfn[x]){//满足这个式子就说明包含x的连通分量已找到，且x是进入该联通分量的第一个节点
//根据low的定义，该连通分量所有点的low都是x，但部分点的low可能不是x
++ans;
while(st.top()!=x){//去除该连通分量的所有点
int now=st.top();
f[now]=ans;
cnt[ans]++;
st.pop();
}
f[st.top()]=ans;
cnt[ans]++;
st.pop();
Max=max(Max,cnt[ans]);
}
}
int main(){
scanf("%d%d",&n,&m);
int a,b,t;
for(int i=1;i<=m;++i){
scanf("%d%d%d",&a,&b,&t);
g[a].push_back(b);
if(t==2)
g[b].push_back(a);
}
for(int i=1;i<=n;++i){
if(!dfn[i])targan(i);
}
for(int i=1;i<=n;++i){
if(cnt[f[i]]==Max){
int a=f[i];
printf("%d\n",cnt[a]);
for(int j=i;j<=n;++j){
if(f[j]==a)printf("%d ",j);
}
return 0;
}
}
return 0;
}
关于low
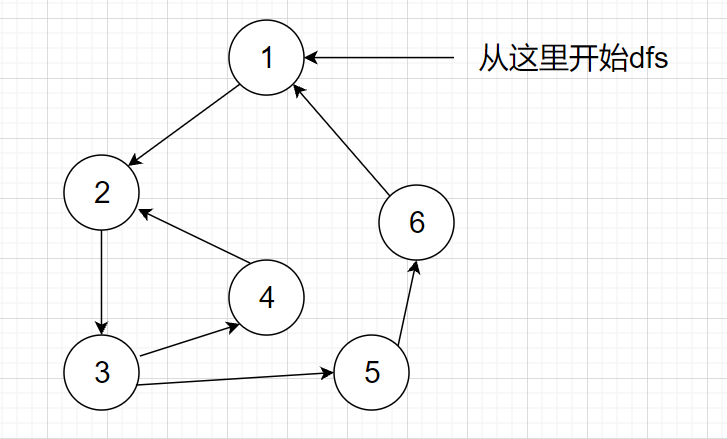
我们可以发现4号点的low是2，而其它节点的low是1，虽然这不会影响最终的结果，
但这有点不符合low的定义。
将low改成:在深搜优先搜索树中当前节点及其子代能访问到的最早结点就行了。
注意这里求得的连通分量是极大连通分量。
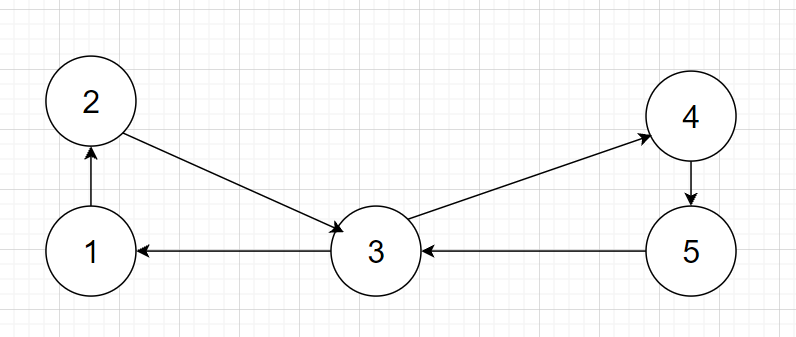
上面这个图只有一个SCC，而不是两个。
