第十一届蓝桥杯大赛第二场省赛试题A组C++&C

试题A：门牌制作

参考代码

#include<bits/stdc++.h>
using namespace std;
int a[10];
void add(int x){
    while(x){
        a[x%10]++;
        x/=10;
    }
}
int main(){
    for(int i=1;i<=2020;++i){
        add(i);
    }
    printf("%d",a[2]);
    return 0;
}

答案：624

试题B：既约分数

参考代码

#include<bits/stdc++.h>
int gcd(int a,int b){
    return b==0?a:gcd(b,a%b);
}
int main(){
    int ans=0;
    for(int i=1;i<=2020;++i)
        for(int j=1;j<=2020;++j){
            if(gcd(i,j)==1)++ans;
        }
        printf("%d",ans);
        return 0;
}

答案：2481215

试题C：蛇形填数

思路
直接模拟。
参考代码

#include<bits/stdc++.h>
using namespace std;
int main(){
    int i=1,j=1,cnt=1,op=0;
    //op==0向上，op==1向下
    //i横坐标j纵坐标
    while(!(i==20&&j==20)){
        if(j==1&&op==0){
            ++i;op=1;
        }
        else if(i==1&&op==1){
            ++j;op=0;
        }
        else if(op==0){
            ++i;--j;
        }
        else {
            --i;++j;
        }
        ++cnt;
    }
    printf("%d",cnt);
    return 0;
}

答案：761

试题D：七段码

思路
每个数码管只有亮与不亮两种选择，故一共有\(2^7\)种可能，枚举每一种情况，检验图是否联通即可(dfs，bfs，并查集...)
参考代码

#include<bits/stdc++.h>
using namespace std;
int g[10][10],book[10],ans,f[10];
void ini(){//建图
    g[1][2]=g[1][6]=1;
    g[2][1]=g[2][7]=g[2][3]=1;
    g[3][2]=g[3][7]=g[3][4]=1;
    g[4][3]=g[4][5]=1;
    g[5][4]=g[5][6]=g[5][7]=1;
    g[6][5]=g[6][1]=g[6][7]=1;
    g[7][2]=g[7][3]=g[7][5]=g[7][6]=1;
}
void check(){//检查下边建错没
    for(int i=1;i<=7;++i)
        for(int j=i+1;j<=7;++j)
        if(g[i][j]!=g[j][i]){
            printf("边建错了");
            exit(0);
        }
}
void dfsg(int x){
    f[x]=1;
    for(int i=1;i<=7;++i)
    if(book[i]&&!f[i]&&g[x][i])dfsg(i);
}
void getans(){
   memset(f,0,sizeof(f));
   for(int i=1;i<=7;++i){
       if(book[i]){dfsg(i);break;}
   }
   int k=1,flag=0;
   for(int i=1;i<=7;++i)
   if(book[i]){
       flag=1;if(!f[i])k=0;
   }
   if(k&&flag)++ans;
}
int getf(int x){
    return x==f[x]?x:f[x]=getf(f[x]);
}
void merge(int a,int b){
    int x=getf(a),y=getf(b);
    f[x]=y;
}
void getans1(){
    for(int i=1;i<=7;++i)f[i]=i;
    for(int i=1;i<=7;++i){
        if(!book[i])continue;
        for(int j=i+1;j<=7;++j){
            if(!book[j])continue;
            if(g[i][j])merge(i,j);
        }
    }
    int k=0;
    for(int i=1;i<=7;++i)if(book[i]&&f[i]==i)++k;
    if(k==1)++ans;
}
void getans2(){
    queue<int>q;
    memset(f,0,sizeof(f));
    for(int i=1;i<=7;++i){
        if(book[i]){q.push(i);f[i]=1;break;}
    }
    while(q.size()){
        int top=q.front();
        q.pop();
        for(int i=1;i<=7;++i){
            if(book[i]&&!f[i]&&g[top][i]){
                q.push(i);f[i]=1;
            }
        }
    }
     int k=1,flag=0;
   for(int i=1;i<=7;++i)
   if(book[i]){
       flag=1;if(!f[i])k=0;
   }
   if(k&&flag)++ans;
}
void dfs(int x){
    if(x==8){
        getans();//dfs
        getans1();//并查集
        getans2();//bfs
        return ;
    }
    book[x]=1;
    dfs(x+1);
    book[x]=0;
    dfs(x+1);
}
int main(){
    /*a b c d e f g
      1 2 3 4 5 6 7*/
    ini();
    check();
    dfs(1);
    printf("%d",ans/3);
    return 0;
}

试题E：平面分割

思路
找规律，我们先看下只有直线的情况。
一条直线分两个部分

两条直线分四个部分

三条直线分七个部分

四条直线分十一个部分

\(\vdots\)
我们可以得到两个规律。
1.要想划分数尽可能多，每条直线与之前直线产生的交点要尽可能多(由于纸无限大，所以每条新加的直线可以与之前的所有直线相交)
2.每新加一条直线，新增的划分数为产生的交点数+1
所以20条直线的划分数为\(2+2+3+4\cdots+20=\frac{(1+20)*20}{2}+1=211\)

再看下同时有直线与圆的情况。
一条直线与一个圆分四个部分

一条直线与两个圆分八个部分

\(\vdots\)
我么们发现一个圆与一条直线或另一个圆一次可产生两个交点。
新加一个圆，新增的划分数为交点个数。
那么20条直线和20个圆产生的划分数为
\((20*2+21*2+\cdots+39*2)+211=1391\)
答案：1391

试题F：成绩分析

参考代码

#include<bits/stdc++.h>
using namespace std;
#define db double
int m,Max,Min=200,sco;
db sum;
int main(){
    scanf("%d",&m);
    for(int i=1;i<=m;++i){
        scanf("%d",&sco);
        sum+=sco;
        Max=max(Max,sco);
        Min=min(Min,sco);
    }
    printf("%d\n%d\n%.2lf",Max,Min,sum/m);
}

试题G：回文日期

思路
枚举前四个字符，找到所有的回文与ababbaba，在二分查找答案即可。
参考代码

#include<bits/stdc++.h>
using namespace std;
int month[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
bool check(int y,int m,int d){
    if(y%4==0&&y%100||y%400)month[2]=29;
    if(m>=1&&m<=12){
        if(month[m]<d)return false;
        return true;
    }
    return false;
}
vector<string>pal;
vector<string>ab;
void ini(){
    int s=1000,e=9999,y,m,d;
    for(int i=s;i<=e;++i){
        string t=to_string(i);
        y=i;
        m=(t[3]-'0')*10+t[2]-'0';
        d=(t[1]-'0')*10+t[0]-'0';
        month[2]=28;
        if(!check(y,m,d))continue;
        for(int j=3;j>=0;--j)t+=t[j];
        pal.push_back(t);
        if(t[0]==t[2]&&t[1]==t[3])ab.push_back(t);
    }
}
int main(){
    ini();
    string a;
    cin>>a;
    cout<<*upper_bound(pal.begin(),pal.end(),a)<<endl;
    cout<<*upper_bound(ab.begin(),ab.end(),a);
}

试题H：字串分值

思路
我们先对样例的一个子串分析一下

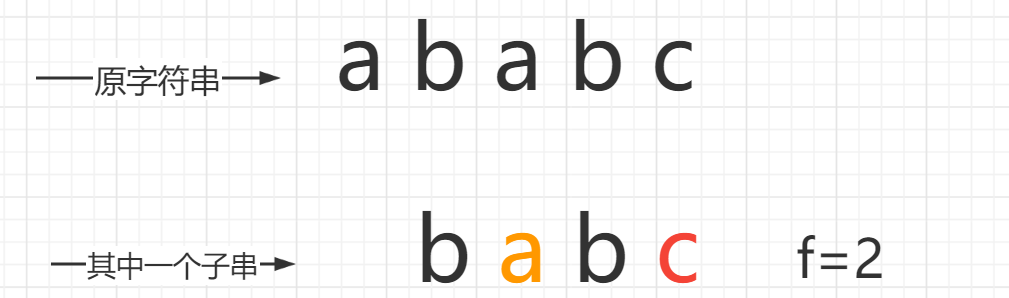
但是光是找出所有子串的时间就已经超时了
换个角度思考一下，babc的f之所以等于2，是因为a,c只出现了一次，
也就是说a,c这两个字母对当前子串分别产生了一个贡献，
这就启示我们去计算每个字母一共在哪些子串里产生了贡献。
我们列出所有a产生贡献的子串。

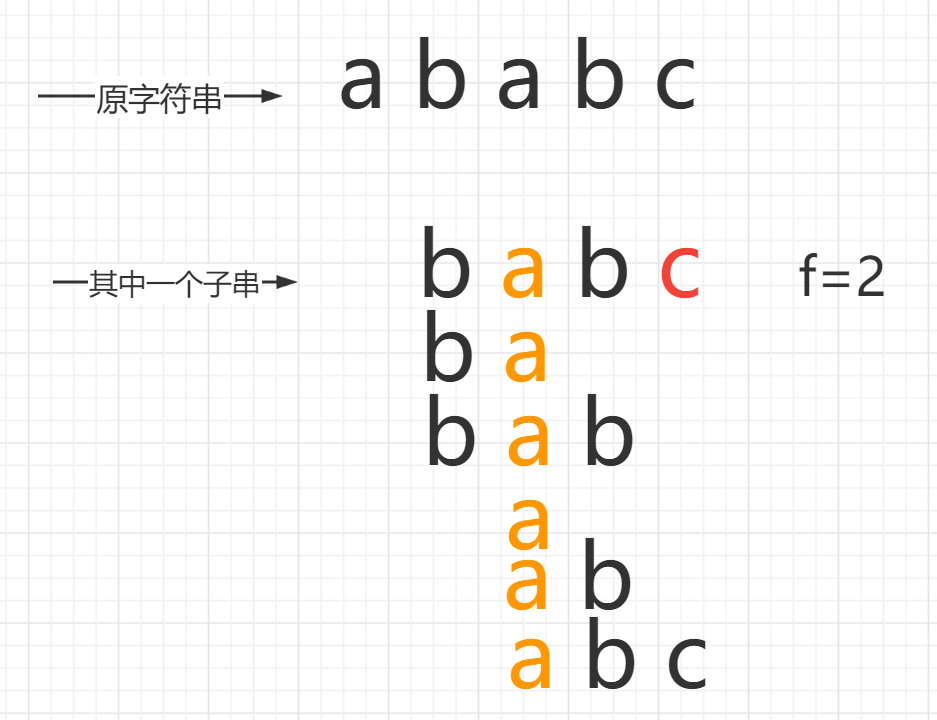
容易发现每个字符的贡献与他上一次与下一次出现的位置有关。

参考代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
char s[N];
int pre[N],nex[N],n;
int book[26];
int main(){
    scanf("%s",s+1);
    n=strlen(s+1);
    for(int i=1;i<=n;++i){
        pre[i]=book[s[i]-'a'];
        book[s[i]-'a']=i;
    }
    for(int i=0;i<26;++i)book[i]=n+1;
    for(int i=n;i>0;--i){
        nex[i]=book[s[i]-'a'];
        book[s[i]-'a']=i;
    }
    long long ans=0;
    for(int i=1;i<=n;++i)
    ans+=1ll*(i-pre[i])*(nex[i]-i);
    printf("%lld",ans);
    return 0;
}   

试题I：荒岛探测

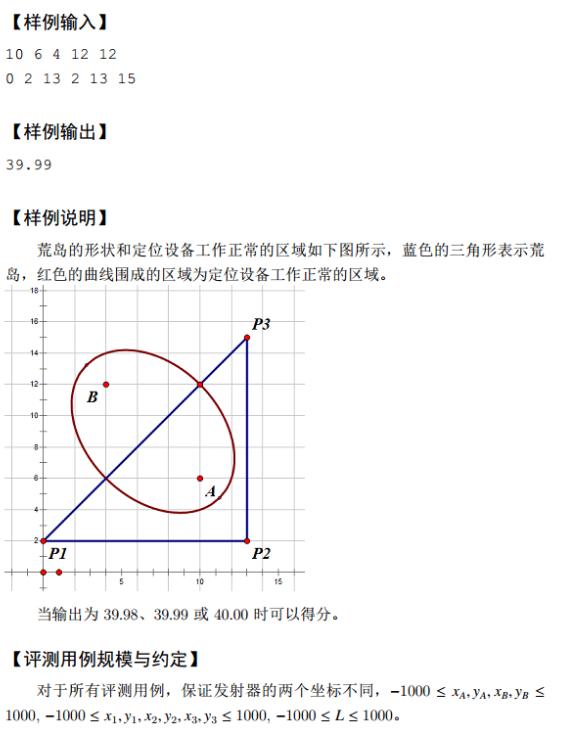
思路
用积分的思想，将目标区域划分成一个个小长方形，因为不需要求精确值，我们使长方形的宽为0.0001左右即可。
还有一个重要的问题，题目中的三角形好说，但是椭圆的焦点及长轴不在x轴上，这个时候求交点就有点麻烦。
我们可以将椭圆平移加旋转，其他点也跟着一起动就行啦。
参考代码

// 荒岛探测
#include<bits/stdc++.h>
using namespace std;
#define db double
const db eps=1e-6;
struct line{
    db A,B,C;
    line(db a,db b,db c):A(a),B(b),C(c){}
    line(){}
};//直线表达式为Ax+By+C=0
struct point{
    db x,y;
    point(db a,db b):x(a),y(b){}
    point(){}
    point operator-(const point &a){
        point t;
        t.x=x-a.x;t.y=y-a.y;
        return t;
    }
    const bool operator<(const point &a)const{
        return x<a.x;
    }
};//存点
struct elp{
    db a,b,c;
    elp(db _a,db _b,db _c):a(_a),b(_b),c(_c){}
    elp(){}
};//椭圆
db xa,ya,xb,yb,L;
line l[5];//保存三条线
point O,tri[3];//新原点，三角行3个点坐标
elp nelp;//新椭圆
db dis(db x1,db y1,db x2,db y2){
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
point get_newpoint(){
    return point((xa+xb)/2,(ya+yb)/2);
}
elp get_newelp(){
    db c=dis(xa,ya,xb,yb)/2;
    db a=L/2;
    return elp(a,sqrt(a*a-c*c),c);
}
void get_line(point &a,point &b,int i){
    if(fabs(a.x-b.x)<eps){
        l[i].A=1;l[i].B=0;l[i].C=-a.x;
    }
    else {
        l[i].B=-1;
        l[i].A=(a.y-b.y)/(a.x-b.x);
        l[i].C=(b.y*a.x-b.x*a.y)/(a.x-b.x);
    }
    return ;
}
void rjd(int a,int b,point &m1,point &m2,db x){
    if(fabs(l[a].B)<eps||fabs(l[b].B)<eps){
        m1.y=min(tri[a].y,tri[b].y);
        m2.y=max(tri[a].y,tri[b].y);
        return ;
    }
    m1.y=l[a].A*x+l[a].C;
    m2.y=l[b].A*x+l[b].C;
    if(m1.y>m2.y)swap(m1,m2);
    return ;
}
int get_tuo(point &m1,point &m2,double x){
    if(fabs(x)>=nelp.a)return -1;
    m2.y=sqrt(nelp.b*nelp.b-nelp.b*nelp.b*x*x/(nelp.a*nelp.a));
    m1.y=-m2.y;
    return 1;
}
int main(){
    scanf("%lf%lf%lf%lf%lf",&xa,&ya,&xb,&yb,&L);
    //这里直接选取椭圆的长轴为新的x轴
    if(xa>xb){swap(xa,xb);swap(ya,yb);}
    O=get_newpoint();
    nelp=get_newelp();
    for(int i=0;i<3;++i){//其他点先平移，在旋转
    scanf("%lf%lf",&tri[i].x,&tri[i].y);
    tri[i]=tri[i]-O;//平移
    }
    xb-=O.x;yb-=O.y;
    db h=-yb;
    db sina=h/nelp.c;
    db cosa=sqrt(1-sina*sina);
    xa=-nelp.c;ya=0;
    xb=nelp.c;yb=0;
    for(int i=0;i<3;++i){
        point temp=tri[i];
        tri[i].x=temp.x*cosa-temp.y*sina;
        tri[i].y=temp.x*sina+temp.y*cosa;
    }
    sort(tri,tri+3);
    //所有点处理完毕
    for(int i=0;i<3;++i){
        get_line(tri[i],tri[(i+1)%3],i);
    }
    db ans=0;
    db l=max(tri[0].x,-nelp.a),r=min(tri[2].x,nelp.a);
    for(double i=l;i<r;i+=0.0001){
        point  m1,m2,m3,m4;
        if(i<tri[1].x){
            rjd(0,2,m1,m2,i);
        }
        else rjd(1,2,m1,m2,i);
        if(get_tuo(m3,m4,i)==-1)continue;
        if(m1.y>m3.y)m3.y=m1.y;
        if(m2.y<m4.y)m4.y=m2.y;
        if(m3.y<m4.y)ans+=(m4.y-m3.y)*0.0001;
    }
    printf("%.2lf\n",ans);
    return 0;
}

试题J：字串排序

思路
首先我们需要知道对一个序列使用冒泡排序的交换次数等于该序列的逆序数。
简单证明一下：冒泡排序每次只会交换相邻的两个元素，不影响其他元素的顺序关系，所以每进行一次交换都会使逆序数减一。
对于该题，有两个步骤，第一步是求出满足交换次数的序列的最小长度，第二步是使该长度的字串的字典序最小。

对于第一步，我们只要求出固定长度的最大交换次数(最大逆序数)即可，要是逆序数最大，很容易想到将所有元素倒着排，
又因为小写字母只有26个，但给定的长度可能远远多于26个，所以要重复使用字母。
下面以三个字母(a,b,c)举例如何重复使用字母使逆序数最大。

序列长度	序列	逆序数
1	a	0
2	ba	1
3	cba	3
4	cbaa	5
5	cbbaa	8
6	ccbbaa	12

规律很明显(不明显的话再多列几组数据)，序列增长的时候，我们要添加当前数量最少的字符才能使逆序数最大。
假设现在要求长度为n的最大逆序数，则所有字母出现的次数为n/26或n/26+1，
且出现次数为n/26+1的字母种类为n%26。

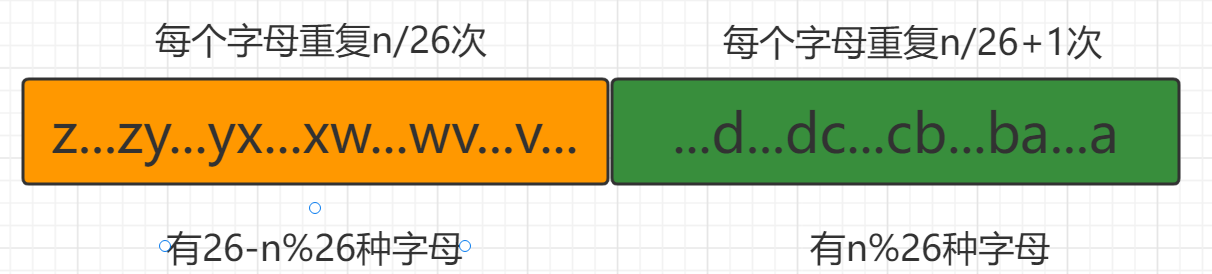
把每种字母产生的逆序数加起来即可得到字串的逆序数。

第二部，为了保证字串的字典序最小，我们可以从左边第一个字符开始枚举，每次从a开始，
枚举的字符我们称之为前缀，后面的字符称之为后缀。
对于每个枚举的前缀，我们都在后缀插入字符使整体的逆序数最大，
如果此时整体最大逆序数小于指定交换次序，那么将当前枚举的字符加一，继续算逆序数。
如果大于指定交换顺序，即可枚举下一位字符。
这个过程一直持续到完(此时后缀长度为0)即可得到答案。

参考代码

#include<bits/stdc++.h>
using namespace std;
char pre[300];// 存前缀
int suf[26];//由于后缀是有规律的，直接记录每个字母出现的次数
int v;
int fun(int len){//返回该长度最大的逆序对数
    int base=26;
    int t=len/base;
    int num=len%26;
    int ans=(25*t+num)*(26*t+num)-num*(t+1);ans/=2;
//没前缀的时候指定长度的最大逆序数公式应该是这样
    return ans;
}
int getinc(int c){//有前缀的时候不能套公式了，要在26个字母中选一个能使逆序数增长最大的字母
    int ans=0,size=strlen(pre);
    for(int i=0;i<size;++i){
        if(c+'a'<pre[i])++ans;
    }
    for(int i=0;i<26;++i)
    if(i!=c)ans+=suf[i];
    return ans;
}
void add(){
    int Max=0,temp=0,ind=0;//每次放一个能使逆序数增长最大的字母
    for(int i=0;i<26;++i){
        suf[i]++;
        if((temp=getinc(i))>Max){
            ind=i;
            Max=temp;
        }
        suf[i]--;
    }
    suf[ind]++;
}
void getmaxstr(int l){
    memset(suf,0,sizeof(suf));//清空后缀
    l-=strlen(pre);//后缀还能放多少个
    while(l){
        add();--l;//一个一个放
    }
}
int getnum(){
    int ans=0,size=strlen(pre);
    for(int i=0;i<size;++i)//前缀的逆序数
        for(int j=i+1;j<size;++j){
            if(pre[i]>pre[j])++ans;
        }
    for(int i=0;i<size;++i)//前缀对后缀
        for(int j=0;j<26;++j){
            if(pre[i]>j+'a')ans+=suf[j];
        }
    int temp=0;
    for(int i=0;i<26;++i){
        ans+=temp*suf[i];
        temp+=suf[i];
    }
    return  ans;
}
void getans(int l){
    for(int i=0;i<l;++i)
        for(int j=0;j<26;++j){//每个位置，一个一个使
            pre[i]=j+'a';
            getmaxstr(l);
            if(getnum()>=v)break;
        }
}
int main(){
    scanf("%d",&v);
    int len=0;
    while(fun(len)<v){
        ++len;
    }
    getans(len);
    printf("%s",pre);
    return 0;
}