二分

简介

二分查找(binary search)，也称折半搜索(half-interval search)，对数搜索(logarithmic search)，是用来在一个有序数组中查找某一元素的算法。

时间复杂度O(log n)

工作原理

在一个有序数组中，每次考察中间的元素(\(\frac{l+r}{2}\))，根据当前元素是否满足题目要求，输出当前元素，在左半边区间查找或在右半边区间查找(三选一）。

在有序数组中查找目标元素

参考代码

// 有序数组为a[n]
// a[n]的元素个数为n
// 目标值为tar
// 假设目标值在数组中最多出现一次
int find(int tar){
    int l=0;//左界
    int r=n-1;//右界
    while(l<=r){
        int mid=(r-l)/2+l;//防止l+r的结果出界
        if(a[mid]==tar)return mid;//找到目标值
        if(a[mid]<tar)l=mid+1;//接下来在右半边查找
        else r=mid+1;//接下来在左半边查找
    }
    return -1;//没找到
}

细节处理

• 判断条件
  若判断条件改为l+1<r，即l与r不相邻。
  
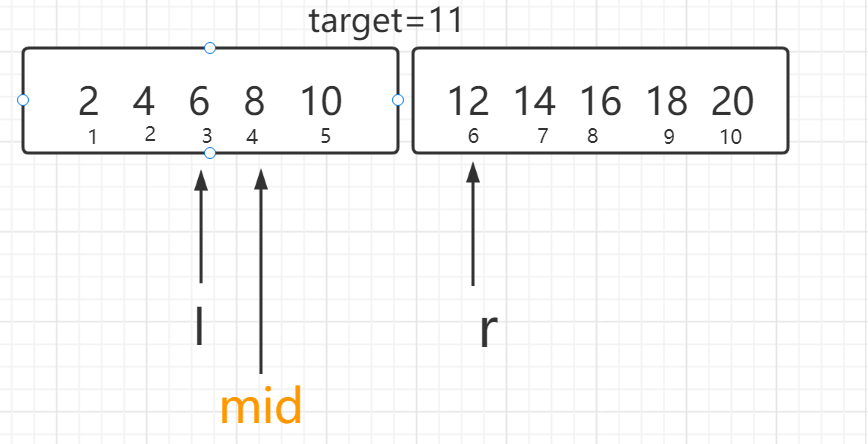
  下一步将变为
  
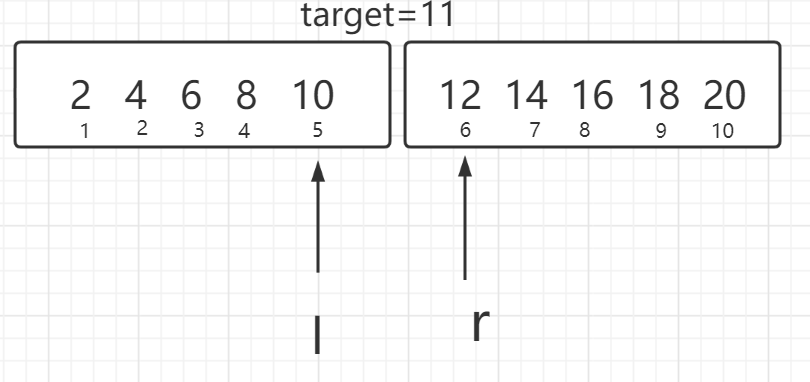
  此时直接跳出循环，容易发现有数据没有判断，当然也可以在返回时特判一下。
  若判断条件改为l<r或l!=r，即l与r重叠时跳出循环。
  
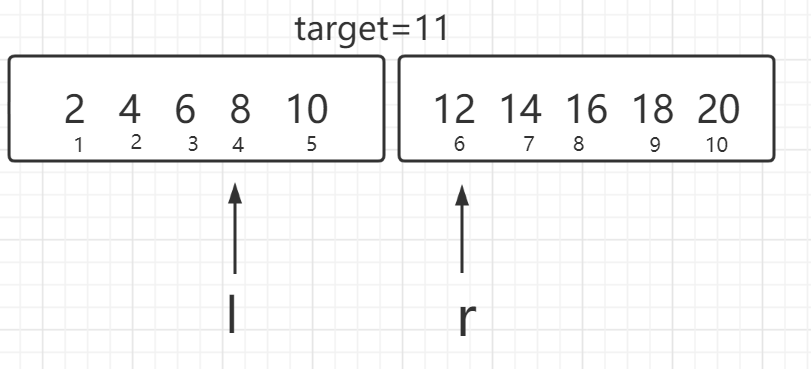
  下一步两个指针重叠并跳出循环，容易发现两个指针指向的数据未检验。

• 转移方式
  若将l=mid+1改为l=mid，此时若两个指针相邻将陷入死循环(当数组中无目标数据时)。
  若将r=mid-1改为r=mid，此时若两个指针重叠将陷入死循环(当数组中无目标数据时)。
  这是因为l与r都是整数，当l+r为奇数时除于2结果将截断。

求解满足条件的最大(小)值

以最大值为例

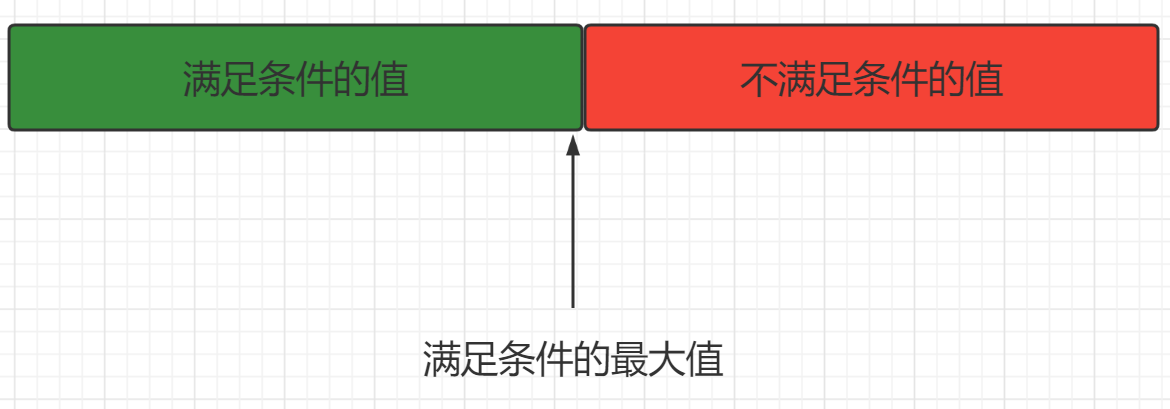
一般情况下，由于数组是单调的，某个元素满足条件时，其左(右)边的所有元素都应该满足条件。
参考代码

int find(int tar){
    int l=0;//左界
    int r=n-1;//右界
    while(l<r){
        int mid=(r-l+1)/2+l;//防止l+r的结果出界
        if(check(mid))l=mid;//check()检验mid是否满足条件
        else r=mid-1;
    }
    return l;
}

细节处理

• 判断条件
  为啥这个时候的判断条件变成l<r即l!=r而不是l<=r呢？
  我们看下当l==r时，由于l指向的元素必满足条件，检验mid时范围不发生变化，又将陷入死循环。

• 转移方式
  l=mid好理解，因为返回的是l指向的元素，所以l指向的元素在每一刻都要满足条件。但这时l与r相邻时不会陷入死循环吗？
  mid=(r-l+1)/2+l当r+l为奇数时，此时mid的0.5将会进1，所以不会陷入死循环。
  r=mid-1，首先为了避免死循环必须这样写，其次因为mid已经不满足条件了，可以踢出搜索范围了。

总结

二分的细节主要有两个。
1.判断条件(防止有数据没检验就跳出循环)
2.转移方式(避免死循环)

补充

C++ lower_bound()函数

lower_bound() 函数用于在指定区域内查找不小于目标值的第一个元素。也就是说，使用该函数在指定范围内查找某个目标值时，最终查找到的不一定是和目标值相等的元素，还可能是比目标值大的元素。

其语法格式有两种：

//在 [first, last) 区域内查找不小于 val 的元素
ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last,const T& val);
//在 [first, last) 区域内查找第一个不符合 comp 规则的元素
ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last,const T& val, Compare comp);

其中，first 和 last 都为正向迭代器，[first, last) 用于指定函数的作用范围；val 用于指定目标元素；comp 用于自定义比较规则，此参数可以接收一个包含 2 个形参（第二个形参值始终为 val）且返回值为 bool 类型的函数，可以是普通函数，也可以是函数对象。

实际上，第一种语法格式也设定有比较规则，只不过此规则无法改变，即使用 < 小于号比较 [first, last) 区域内某些元素和 val 的大小，直至找到一个不小于 val 的元素。这也意味着，如果使用第一种语法格式，则 [first,last) 范围的元素类型必须支持 < 运算符。
此外，该函数还会返回一个正向迭代器，当查找成功时，迭代器指向找到的元素；反之，如果查找失败，迭代器的指向和 last 迭代器相同。

再次强调，该函数仅适用于已排好序的序列。所谓“已排好序”，指的是 [first, last) 区域内所有令 element<val（或者 comp(element,val)，其中 element 为指定范围内的元素）成立的元素都位于不成立元素的前面。
举例：

#include <iostream>     // std::cout
#include <algorithm>    // std::lower_bound
#include <vector>       // std::vector
using namespace std;
//以普通函数的方式定义查找规则
bool mycomp(int i,int j) { return i>j; }
//以函数对象的形式定义查找规则
class mycomp2 {
public:
    bool operator()(const int& i, const int& j) {
        return i>j;
    }
};
int main() {
    int a[5] = { 1,2,3,4,5 };
    //从 a 数组中找到第一个不小于 3 的元素
    int *p = lower_bound(a, a + 5, 3);
    cout << "*p = " << *p << endl;
    vector<int> myvector{ 4,5,3,1,2 };
    //根据 mycomp2 规则，从 myvector 容器中找到第一个违背 mycomp2 规则的元素
    vector<int>::iterator iter = lower_bound(myvector.begin(), myvector.end(),3,mycomp2());
     //或使用mycomp
 //vector<int>::iterator iter = lower_bound(myvector.begin(), myvector.end(),3,mycomp);
    cout << "*iter = " << *iter;
    return 0;
}
//结果
//*p = 3
//*iter = 3

myvector中的元素看似是乱序的，但对于mycomp2()而言，满足此规则(大于3的元素)都在左边，不满足(小于等于3)在右边。

upper_bound()函数与lower_bound()函数的唯一区别在于第一种语法规则，upper_bound()返回的一个大于目标元素的值。
第二种语法规则中二者都是找到第一个不满足自定义规则的元素。

在第一种语法规则中，关于两个函数另一种等效的解释：
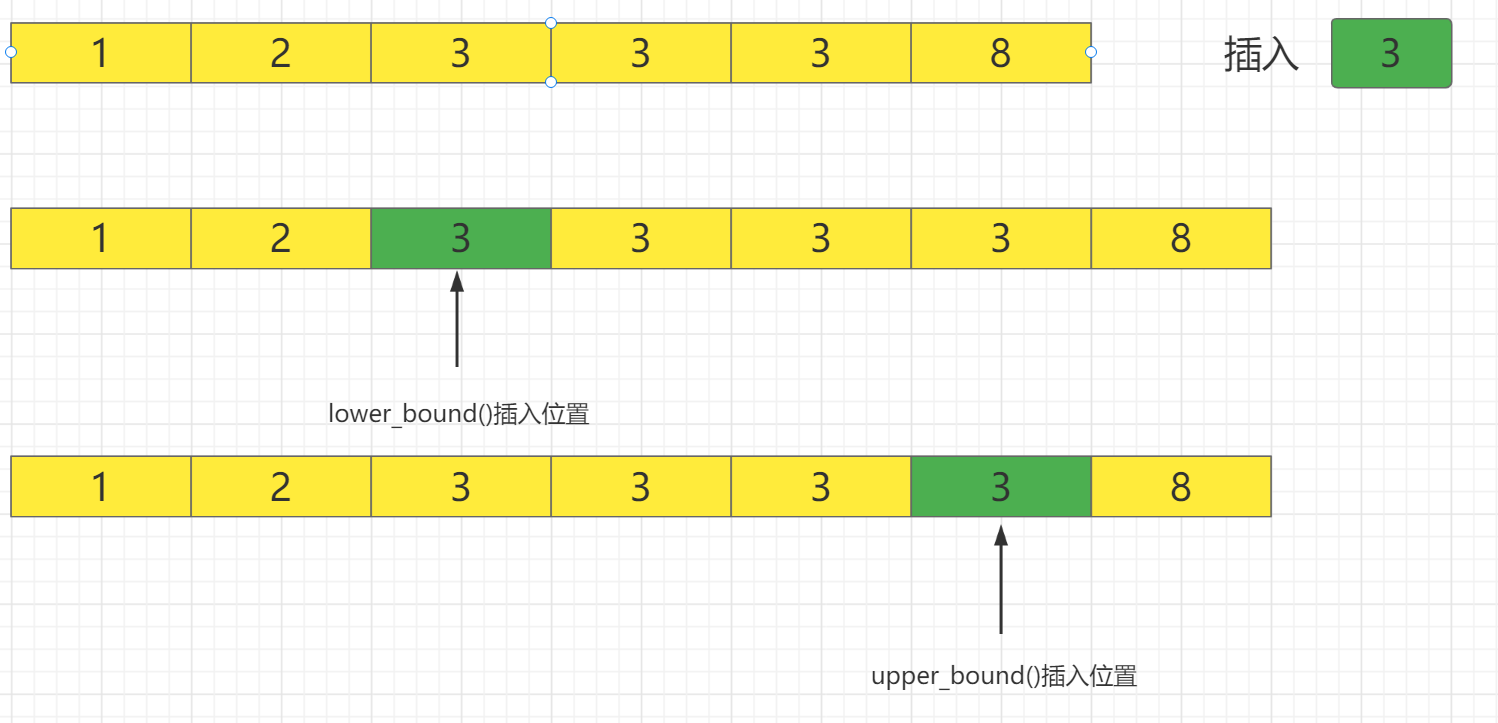
在一个有序序列中(升序)，upper_bound()返回最后一个目标元素可插入的位置。
lower_bound()返回第一个目标元素可插入的位置。

更新

二分模板（无论找目标值或最大最小可行值都可）以前写的太复杂了

while(l<=r){
		int mid=(l+r)/2;
		if(check(mid)){
			ans=mid;//左区间满足ans在这里赋值，右区间满足放下面，找可行解不用ans
			l=mid+1;
		}
		else {
			r=mid-1;
		}
	}