第十二届蓝桥杯大赛软件赛省赛
试题A:卡片

题解
#include<bits/stdc++.h>
using namespace std;
int a[10];
bool check(int x){
while(x){
int t=x%10;
if(!a[t])return false;
--a[t];
x/=10;
}
return true;
}
int main(){
for(int i=0;i<10;++i)a[i]=2021;
int ans=0;
while(1){
++ans;
if(!check(ans))break;
}
cout<<ans-1;
return 0;
}
答案:3181
试题B:直线

题解
法一
手动设置精度,小于该精度即认为相等
#include<bits/stdc++.h>
using namespace std;
#define db double
struct no{
int x,y;
no(int a,int b):x(a),y(b){}
};
db eps=1e-6;
vector<no>point;
vector<pair<db,db>>ans;
int main(){
for(int i=0;i<20;++i)
for(int j=0;j<21;++j){
point.push_back(no(i,j));
}
int tot=point.size();
for(int i=0;i<tot;++i)
for(int j=i+1;j<tot;++j){
db x1=point[i].x,y1=point[i].y;
db x2=point[j].x,y2=point[j].y;
if(x1==x2||y1==y2)continue;
db k=(y1-y2)/(x1-x2);
db b=y1-k*x1;
int flag=1;
for(int c=0;c<ans.size();++c){
if(fabs(k-ans[c].first)<eps&&fabs(b-ans[c].second)<eps){
flag=0;break;
}
}
if(flag)ans.push_back(make_pair(k,b));
}
cout<<ans.size()+20+21;
return 0;
}
法二
修改b的表达式:\(b=\frac{y_2*x_1-y_1*x_2}{x_1-x_2}\),就像\(\frac{2}{3} = \frac{4}{6}\)防止误差产生。
#include<bits/stdc++.h>
using namespace std;
#define db double
struct no{
int x,y;
no(int a,int b):x(a),y(b){}
};
db eps=1e-6;
vector<no>point;
set<pair<db,db>>ans;
int main(){
for(int i=0;i<20;++i)
for(int j=0;j<21;++j){
point.push_back(no(i,j));
}
int tot=point.size();
for(int i=0;i<tot;++i)
for(int j=i+1;j<tot;++j){
db x1=point[i].x,y1=point[i].y;
db x2=point[j].x,y2=point[j].y;
if(x1==x2||y1==y2)continue;
db k=(y1-y2)/(x1-x2);
db b=(y2*x1-y1*x2)/(x1-x2);
int flag=1;
ans.insert({k,b});
}
cout<<ans.size()+20+21;
return 0;
}
答案:40257
试题C:货物摆放

题解
数字超级大,但质因数只有8个,因数只有128个,暴力枚举即可
顺便说一下因数个数等于不同质因数的指数分别加1后相乘的积
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2021041820210418;
ll prime[100],divs[1000];
int myexp[100];
int cntp,cntd;
void get_p(){
ll x=N;
for(int i=2;i*i<=x;++i){
if(x%i==0){
prime[cntp]=i;
while(x%i==0)myexp[cntp]++,x/=i;
++cntp;
}
}
if(x>1)prime[cntp]=x,myexp[cntp++]=1;
}
void dfs(int now,ll tot){
if(now>=cntp){
divs[cntd++]=tot;
return ;
}
ll base=1;
for(int i=0;i<=myexp[now];++i){
dfs(now+1,tot*base);
base*=prime[now];
}
}
int ans=0;
int main(){
get_p();
printf("质因数有%d个:\n",cntp);
for(int i=0;i<cntp;++i)printf("%d ",prime[i]);
putchar('\n');
dfs(0,1);
printf("因数有%d个:\n",cntd);
for(int i=0;i<cntd;++i)printf("%lld ",divs[i]);
putchar('\n');
for(int i=0;i<cntd;++i)
for(int j=0;j<cntd;++j)
for(int k=0;k<cntd;++k)
if(divs[i]*divs[j]*divs[k]==N)++ans;
printf("答案:%d",ans);
return 0;
}
答案:
试题D:路径

题解
求最短路常用的三种方法:
1.弗洛伊德(Floyd-Warshall algorithm)多源最短路
2.spfa(贝尔曼福特(Bellman-Ford)的队列优化)单源最短
3.迪杰斯特拉(Dijkstra)单源最短
这里贴一个dijkstra
#include<bits/stdc++.h>
using namespace std;
const int N=2050;
struct no{
int x,id;
no(int a,int b):id(a),x(b){}
no(){}
const bool operator<(const no&a)const{
return x>a.x;//与小根堆配套使用
}
};
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
int g[N][N],dis[N],book[N];
priority_queue<no>q;
void dij(){
dis[1]=0;
q.push(no(1,0));
while(q.size()){
no now=q.top();
q.pop();
if(book[now.id])continue;
book[now.id]=1;
for(int i=1;i<=2021;++i){
if(dis[i]>dis[now.id]+g[now.id][i]){
dis[i]=dis[now.id]+g[now.id][i];
q.push(no(i,dis[i]));
}
}
}
}
int main(){
memset(dis,0x3f,sizeof(dis));
memset(g,0x3f,sizeof(g));
for(int i=1;i<=2021;++i)
for(int j=i+1;j<=i+21;++j){
g[i][j]=i*j/gcd(i,j);
g[j][i]=g[i][j];
}
dij();
cout<<dis[2021];
return 0;
}
答案:10266837
试题E:回路计数

题解
状压 dp 是动态规划的一种,通过将状态压缩为整数来达到优化转移的目的。 ---OI Wiki
状态压缩的思想是用二进制来表示状态。用一个整数的二进制形式的每一个0或1表示一个状态。
f[i][j]表示当前处在点i状态为j
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=21;
const int M=1<<N;
int g[N][N];
int gcd(int a,int b){
return b?gcd(b,a%b):a;
}
ll f[N][M];
int main(){
for(int i=0;i<N;++i)
for(int j=i+1;j<N;++j){
if(gcd(i+1,j+1)==1)g[i][j]=g[j][i]=1;
}
f[0][1]=1;
for(int i=2;i<M;++i)//从小到大遍历每一种状态
for(int j=0;j<N;++j){
if((i&(1<<j))==0)continue;
for(int k=0;k<N;++k){
if((i&(1<<k))==0||j==k)continue;
if(g[j][k]) f[j][i]+=f[k][i-(1<<j)];
}
}
ll ans=0;
for(int i=1;i<N;++i)ans+=f[i][M-1];
cout<<ans;
return 0;
}
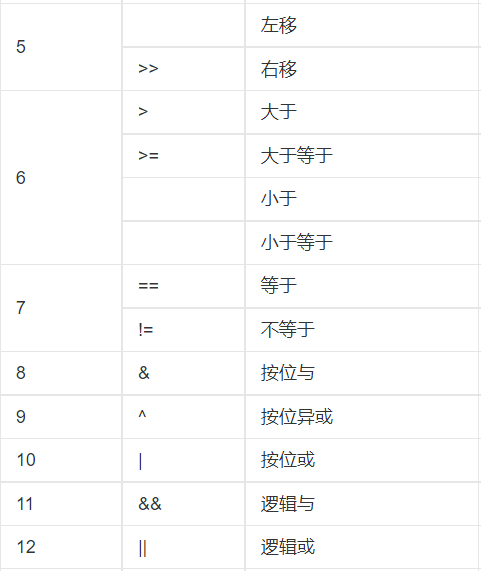
注意==优先级高于&
答案:881012367360
试题F:砝码称重

题解
动态规划
f[i][j]表示前i个砝码是否能称重j
注意状态转移方程有三个
若前i-1个砝码能表示质量x
则增加一个砝码后
1.\(x+a[i]\)
2.\(x-a[i](x>=a[i])\)
3.\(a[i]-x(a[i]>=x)\)
能表示以上三种质量
#include<bits/stdc++.h>
using namespace std;
const int N=105;
const int M=1e5+5;
bool f[N][M];
int a[N],tot;
int main(){
int n;
cin>>n;
for(int i=1;i<=n;++i)cin>>a[i],tot+=a[i];
f[0][0]=1;//初始化
for(int i=1;i<=n;++i)
for(int j=0;j<=tot;++j){
f[i][j]|=f[i-1][j];//继承一下前面的值
if(j>=a[i])f[i][j]|=f[i-1][j-a[i]];
if(j+a[i]<=tot)f[i][j]|=f[i-1][j+a[i]];
if(a[i]>=j)f[i][j]|=f[i-1][a[i]-j];
}
int ans=0;
for(int i=1;i<=tot;++i)ans+=f[n][i];
cout<<ans;
return 0;
}
试题G:异或数列

对于所有评测用例,\(1\le T\le 2e5\),\(1 \le \sum^T_{i=1}n_i \le 2e5\),\(0 \le X_i \le 2^{20}\).
题解
对于此类问题的两个思考方向
1.记忆化搜索
2.找规律
显然记忆化搜索空间不够而且太复杂,所以我们找规律
注意到无论哪种分配方式,两名玩家的数列异或起来的值为定值,若该值为0,则必定平局。(两个数字异或等于0,则两个数字相等)
现在考虑所有数字的二进制,用count记录所有数字异或结果的位数,用flag记录所有数字中,位数为count的个数,size为所有数字的个数。(位数为count的数简称count数)
首先可以得到flag必为奇数且count数对答案有关键影响,因为位数比count高的位在异或之后会抵消。
1.\(flag==1\),则先手必赢,只要他拿到这个数就获得了异或结果的最高位。
2.\(size\%2==1\),先手赢,先手只要先拿一个count数就可以采用策略是自己手中的count数的个数位奇。
3.\(size\%2==0\),后手赢,因为后手可以采用策略是自己手中的count数的个数为奇。
#include<bits/stdc++.h>
using namespace std;
int main(){
int T;
cin>>T;
while(T--){
vector<int>a;
int n;
cin>>n;
for(int i=0;i<n;++i){
int temp;cin>>temp;a.push_back(temp);
}
int sum=0;
for(auto i:a)sum^=i;
if(sum==0){
cout<<0<<endl;continue;
}
int count=0;
while(sum){
sum>>=1;++count;
}
int flag=0;
for(auto i:a){
if((i>>(count-1))&1)++flag;
}
if(flag==1){cout<<1<<endl;continue;}
if(a.size()%2)cout<<1<<endl;
else cout<<-1<<endl;
}
return 0;
}
试题H:左孩子右兄弟


题解
树形DP
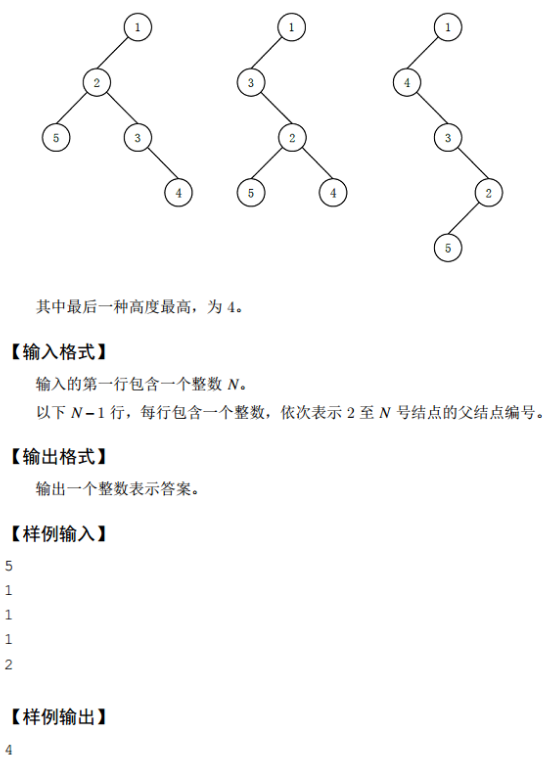
用f[i]表示以i为根节点。转化为二叉树的高度。则有:
f[i]=i的孩子节点个数+max(f[j]),j为i的孩子节点
从样例中可以很直观的看出i的孩子节点个数为f[i]的一部分,只要将最大的f[j]放到最下面,就可以得到上式。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int f[N],n;
vector<int>g[N];
int dfs(int x){
f[x]+=g[x].size();
int res=0;
for(int i=0;i<g[x].size();++i){
res=max(dfs(g[x][i]),res);
}
f[x]+=res;
return f[x];
}
int main(){
cin>>n;
int t;
for(int i=2;i<=n;++i){
cin>>t;
g[t].push_back(i);
}
dfs(1);
cout<<f[1];
}
试题I:括号序列

y总的视频
题解
合法括号序列需要满足的两条性质:
1.左括号总数等于右括号总数
2.任意前缀序列中左括号数大于等于右括号数
令cnt=左括号数-右括号数,从左向右遍历整个序列并维护cnt。
当cnt<0时,不满足性质2,则当前位置之前必须添加若干左括号使\(cnt\ge0\),遍历完之后若cnt>0则在添加若干右括号。
我们先考虑添加左括号,f[i][j]表示第i个右括号前添加j个左括号的方案数
add[i]表示第i个右括号前至少应添加的左括号数。
f[i][j]=f[i-1][0]+f[i-1][1]\(\cdots\)f[i-1][j]
那么就得到了\(n^3\)的算法
for(int i=1;i<=num;++i)//num为右括号的个数
for(int j=add[i];j<=len;++j)//len为括号总数
for(int k=0;k<=j;++k){
f[i][j]+=f[i-1][k];
}
但过不了5k的数据
f[i][j]=f[i-1][0]+f[i-1][1]\(\cdots\)f[i-1][j]
f[i][j+1]=f[i-1][0]+f[i-1][1]\(\cdots\)f[i-1][j+1]
则有f[i][j+1]=f[i][j]+f[i-1][j+1]
此时算法复杂度降低到了\(n^2\)
添加右括号时,我们将字符串反转,左括号变为右括号,右括号变为左括号,再调用相同的算法即可。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=5e3+5;
const int mod=1e9+7;
char s[N];
int len;
int add[N];
int f[N][N];
ll work(){
int num=0,cntl=0,cntr=0;
memset(add,0,sizeof(add));
memset(f,0,sizeof(f));
for(int i=1;i<=len;++i){
if(s[i]=='('){
++cntl;
}
else {
++num;
++cntr;
if(cntl)--cntl,--cntr;
add[num]=cntr;
}
}
if(!num)return 1;//这里注意一下
for(int i=add[1];i<=len;++i)f[1][i]=1;//初始化
for(int i=1;i<=num;++i){
for(int j=0;j<=add[i];++j)
f[i][add[i]]=(f[i][add[i]]+f[i-1][j])%mod;//第一个值单独计算
for(int j=add[i]+1;j<=len;++j)
f[i][j]=(f[i][j-1]+f[i-1][j])%mod;
}
return f[num][add[num]];
}
int main(){
scanf("%s",s+1);
len=strlen(s+1);
ll l=work();
reverse(s+1,s+1+len);
for(int i=1;i<=len;++i)
if(s[i]=='(')s[i]=')';
else s[i]='(';
ll r=work();
cout<<(l*r)%mod;
return 0;
}
试题J:分果果
不会

