编译原理系列 实验三自下而上语法分析
系列第三弹!
实验三 自下而上语法分析
实验目的
- 给出 PL/0 文法规范,要求编写 PL/0 语言的语法分析程序。
- 通过设计、编制、调试一个典型的自下而上语法分析程序,实现对词法分析程序所提供的单词序列进行语法检查和结构分析,进一步掌握常用的语法分析方法。
- 选择最有代表性的语法分析方法,如算符优先分析法、LR 分析法;或者调研语法分析器的自动生成工具 YACC 的功能与工作原理,使用 YACC 生成一个自底向上的语法分析器。
题目
【问题描述】
考虑到大家用的编程语言不同,且实验一有少数同学没有得到正确结果,为不影响实验三的开展,实验三的输入统一采用词法分析器的输出结果为输入,输入形式如下:
【输入形式】
(lparen,()
(ident,a)
(plus,+)
(number,15)
(rparen,))
(times,*)
(ident,b)
【输出形式】
对于语法正确的表达式,报告“语法正确”,输出为“Yes,it is correct.”
对于语法错误的表达式,报告“语法错误”,输出为“No,it is wrong.”
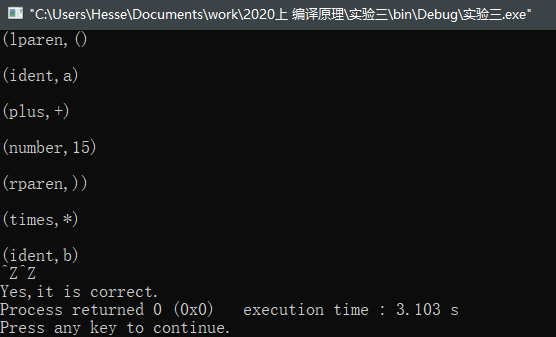
【样例输入】
(lparen,()
(ident,a)
(plus,+)
(number,15)
(rparen,))
(times,*)
(ident,b)
【样例输出】
Yes,it is correct.
【测试数据】
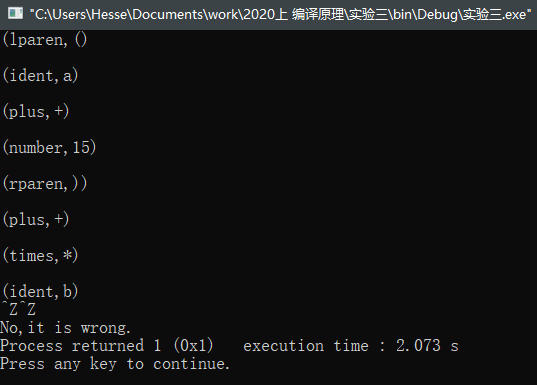
系统给出两组测试数据:测试数据1:如以上样例输入输出;测试数据2的输入为:
(lparen,()
(ident,a)
(plus,+)
(number,15)
(rparen,))
(plus,+)
(times,*)
(ident,b)
测试数据2的输出为:
No,it is wrong.
源程序
优先关系表是手工算的。
#include <iostream>
#include <string.h>
#include<bits/stdc++.h>
#define N_VT 9
using namespace std;
// 优先关系表
int findP(int a, int b) // a、b ∈ [1,9],之所以从1开始,是要适应in_vt的返回值
{
int table[N_VT][N_VT] = // 1表示>,-1表示<,0表示=,2表示空
{{0,0,-1,-1,-1,-1,-1,1,1},
{0,0,-1,-1,-1,-1,-1,1,1},
{1,1,0,0,-1,-1,-1,1,1},
{1,1,0,0,-1,-1,-1,1,1},
{1,1,1,1,0,2,2,1,1},
{1,1,1,1,2,0,2,1,1},
{-1,-1,-1,-1,-1,-1,-1,0,1},
{1,1,1,1,2,2,0,1,1},
{-1,-1,-1,-1,-1,-1,-1,-1,0}};
return table[a-1][b-1];
}
// 检查c是否是终结符,如果不是,返回0,如果是,返回它在算符优先表中的行号(从1开始)
int in_vt(char c)
{
int n;
switch(c)
{
case 'p': n=1; break;
case 'm': n=2; break;
case 't': n=3; break;
case 's': n=4; break;
case 'i': n=5; break;
case 'n': n=6; break;
case 'l': n=7; break;
case 'r': n=8; break;
case '#': n=9; break;
default: n=0;
}
return n;
}
// 判断表达式的合法性
// p指向分析栈的首部,k指向栈顶;psc指向输入符号
// 暂时没有考虑到括号的匹配
int judge(char* p, int k, char* psc)
{
if(k == 1 && p[k] == '#' && (*psc == 'p' || *psc == 'm' || *psc == 't' || *psc == 's'))
{
//printf("\n运算符前面没有操作数!\n");
return 0;
}
if(*psc == '#' && (*(psc-1) == 'p' || *(psc-1) == 'm' || *(psc-1) == 't' || *(psc-1) == 's'))
{
//printf("\n运算符后面没有操作数!\n");
return 0;
}
if(((*psc == 'p' || *psc == 'm' || *psc == 't' || *psc == 's') && ((*(psc+1) == 'p' || *(psc+1) == 'm' || *(psc+1) == 't' || *(psc+1) == 's'))))
{
//printf("\n运算符号相邻!\n");
return 0;
}
return 1;
}
void getinputs(char* in_c)
{
int i = 0;
string line;
while(cin >> line)
{
in_c[i++] = line[1];
}
in_c[i] = '#';
}
// 总控程序
int main()
{
// 分析栈
char s[30] = {'\0'};
int k = 1; // 指向栈顶
s[k] = '#';
s[k+1] = '\0';
int j; // 指向栈顶终结符
char q; // j指向的元素,即栈顶终结符
// 输入处理
char in_c[50] = {'\0'}; // 输入串
//printf("字符串是:%s\n", in_c);
char *psc = in_c; // 指向当前输入符号
int flag; // 查算符优先表得到的值(1/-1/0/2)(大于/小于/等于/空)
// 分析总控程序
while(1)
{
if(!judge(s, k, psc))
{
printf("No,it is wrong.");
exit(1);
}
// 让j正确指向栈顶非终结符
if(in_vt(s[k]))
j = k;
else
j = k-1;
// 根据s[j]和*psc的优先关系,判断移进规约
flag = findP(in_vt(s[j]), in_vt(*psc));
if(flag == 1) // s[j] > *psc,规约
{
// 找到规约范围
do{
q = s[j];// q保存当前的终结符
// j向下探一(两)步,找到下一个终结符
if(in_vt(s[j-1]))
j--;
else
j-=2;
}while(findP(in_vt(s[j]), in_vt(q)) != -1);
// 规约
k = j+1;
s[k] = 'N'; // 管它规约成了哪个非终结符,不重要
s[k+1] = '\0';
continue;
}
else if(flag == -1)// s[j] < *psc,移进
{
k++;
s[k] = *psc;
s[k+1] = '\0';
psc++;
continue;
}
else if(flag == 0)
{
if(s[j] == '#')
{
printf("Yes,it is correct.");
break;
}
else // 否则移进
{
k++;
s[k] = *psc;
s[k+1] = '\0';
psc++;
continue;
}
}
else // 优先级表中空的地方
{
printf("No,it is wrong.");
exit(1);
}
}
return 0;
}
实验结果