初识numpy二
一、Numpy 数组的基本操作
1.1索引
一维与列表完全一致
import numpy as np import matplotlib.pyplot as plt sanpang = plt.imread('./jinzhengen.png') sanpang
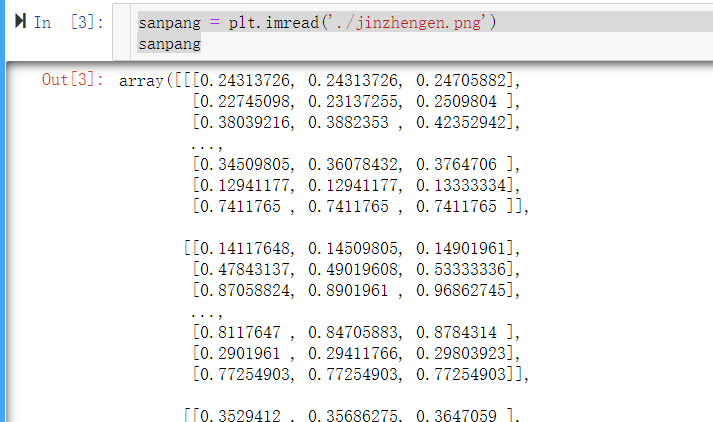
ndarray 对比 list
#ndarray对比list li_ = [1,2,3,4,[0,1,2,[2,3,4]]] li_ # [1, 2, 3, 4, [0, 1, 2, [2, 3, 4]]] li_[-1][-1][-1] # 4 sanpang[0][0][0] # 0.24313726
#ndarray的索引是取决于维度的,维度越多,索引的值越多
sanpang[0,0,-1]
# 0.24705882
案例:颠倒图片
plt.imshow(sanpang)
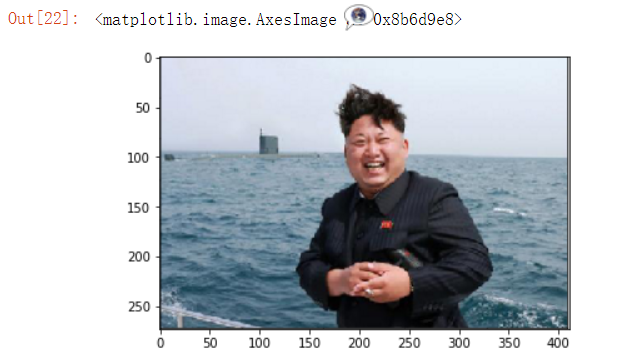
#第一个维度代表的是行,第二个维度代表的是列,第三个维度rgb=bgr plt.imshow(sanpang[::-1,::-1,::-1])

马赛克
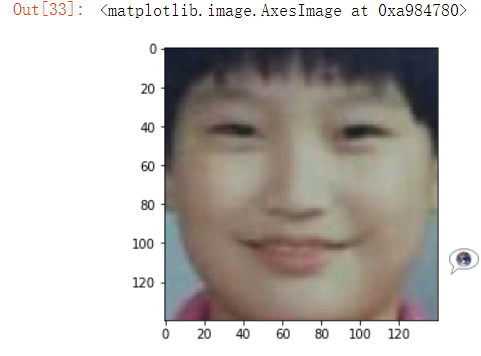
#加了一层蒙版 sanpang.shape # (273, 411, 3) guobin = plt.imread('./guobin.jpg') plt.imshow(guobin)

plt.imshow(guobin[100:240,45:185])
gb = guobin.copy() for i in range(7): for j in range(7): #边遍历边覆盖 gb[100+20*i:20*i+120,45+20*j:20*j+65] = gb[100+20*i:20*i+120,45+20*j:20*j+65][::20][::20]
plt.imshow(gb)

把guobin的脸换成狗脸
dog = plt.imread('dog.jpg') plt.imshow(dog)
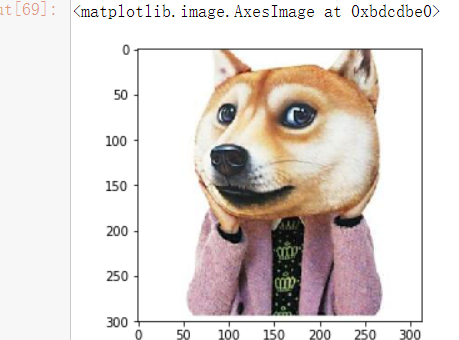
dog_ = dog.copy() dog_face = dog_[40:180,70:210] plt.imshow(dog_face)
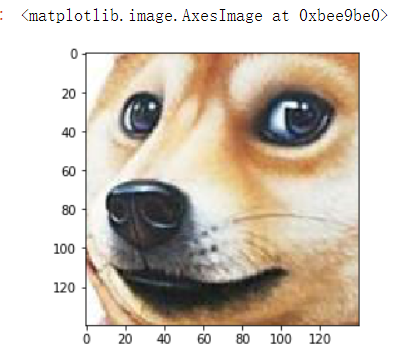
gb[100:240,45:185] = dog_face
plt.imshow(gb)

重设形状
reshape 可以在不改变数组数据的同时,改变数组的形状。其中,numpy.reshape() 等效于 ndarray.reshape()。reshape方法非常简单:
gb.shape # (405, 259, 3) #将三维图片变为2维图片 #改变形状的时候,样本的总个数不能少,二维的图片的是黑白,plt.imshow()方法中有额外的色素 plt.imshow(gb.reshape(405,259*3),cmap='gray') #改变形状的方法不能处理图片的灰度化

#reshape仅仅只能改变数组的形状 gb.reshape(405,-1)
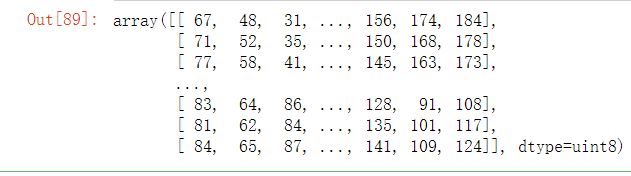
gb.reshape((405,-1)).shape # (405, 777) gb.reshape(405,259*3).shape # (405, 777) #将上述的三维数组变成一维的数组 #-1默认将所有的维度自动相乘 gb.reshape(-1) # array([ 67, 48, 31, ..., 141, 109, 124], dtype=uint8)
数组展开
ravel 的目的是将任意形状的数组扁平化,变为 1 维数组。ravel 方法如下:
不管是几维的数组都会变成1维的数据
gb.ravel() # array([ 67, 48, 31, ..., 141, 109, 124], dtype=uint8)
2.2级联
- np.concatenate() 级联需要注意的点:
- 级联的参数是列表:一定要加中括号或小括号
- 维度必须相同
- 形状相符
- 【重点】级联的方向默认是shape这个tuple的第一个值所代表的维度方向
- 可通过axis参数改变级联的方向,默认为0, (0表示列相连,表示的X轴的事情,1表示行相连,Y轴的事情)
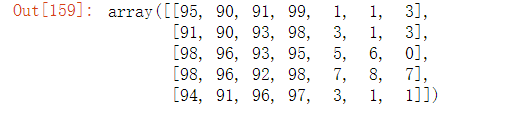
nd1 = np.random.randint(90,100,size=(5,4)) nd2 = np.random.randint(0,10,size=(5,3)) display(nd1,nd2)

#0叫做行方向的拼接,1是列方向上的拼接 np.concatenate((nd1,nd2),axis=1)
不同行数的数组合并¶
nd3 = np.random.randint(30,40,size=(4,4))
nd3

np.concatenate((nd3,nd1),axis=0)

将人和狗的图片合并
jpg 格式转成png格式图片需要乘以255
sanpang = plt.imread('./jinzhengen.png') sanpang.shape # (273, 411, 3) dog = plt.imread('./dog.jpg') dog = dog/255 #切开 dog_ = dog.copy() plt.imshow(np.concatenate((dog_[:273],sanpang),axis=1))

例如:
plt.imshow((sanpang*255).astype(np.uint8)) #jpg 0-255 uint8
numpy.[hstack|vstack]
堆 做级联
分别代表水平级联与垂直级联,填入的参数必须被小括号或中括号包裹
vertical垂直的 horizontal水平的 stack层积
这两个函数的值也是一个list或tuple
plt.imshow(np.hstack((dog_[:273],sanpang)))

分割数组
numpy.split(array,[index1,index2,.....],axis)
axis默认值为0,表示垂直轴,如果值为1,表示水平的轴
注意:indices_or_sections ->[100,200]列表中有两个值,第一个值代表0:100,第二个值代表100:200,后面还有一个值200: 会产生三个值,三个值需要三个变量来接受。
例题,将人水平切成3份
plt.imshow(sanpang)
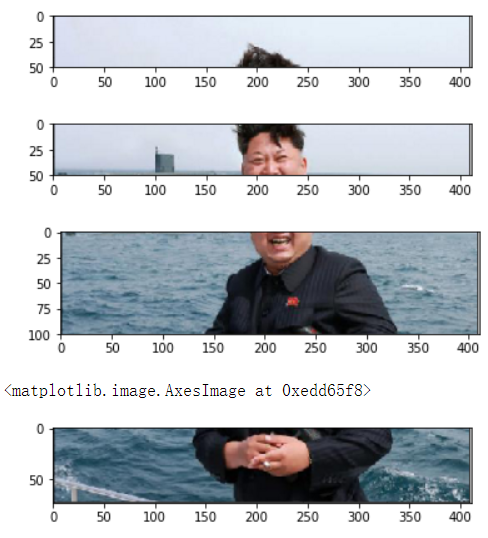
#序列 list tuple k1,k2,k3,k4 = np.split(sanpang,[50,100,200],axis=0) #jupyter 默认只打印最低端的变量 plt.imshow(k1) plt.show() plt.imshow(k2) plt.show() plt.imshow(k3) plt.show() plt.imshow(k4)
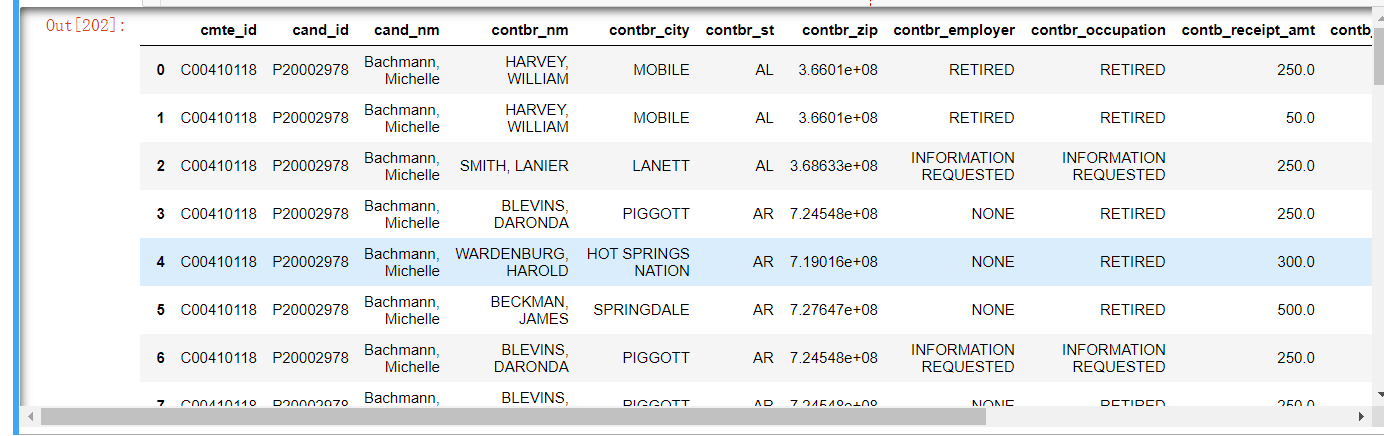
分割数据
import pandas as pd data_ = pd.read_csv('./usa_election.csv') f50,l_=np.split(data_,[50]) f50
副本
所有赋值运算不会为ndarray的任何元素创建副本。对赋值后的对象的操作也对原来的对象生效。
可使用ndarray.copy()函数创建副本
fish_ = plt.imread('fish.png') fish_Backup = fish_.copy() #副本的作用是在开发的时候,对不了解的数据结构做一个备份,防止在后续的处理中操作失误 for i in range(10): fish_Backup[i]=0 plt.imshow(fish_[:250])
ndarray的聚合函数
1.14.1 1. 求和np.sum
ndarray.sum(axis),axis不写则为所有的元素求和,为0表示行求和,1表示列求和
nd4 = np.ones(shape=(5,4)) nd4 # array([[1., 1., 1., 1.], [1., 1., 1., 1.], [1., 1., 1., 1.], [1., 1., 1., 1.], [1., 1., 1., 1.]]) nd4.sum(axis=-2) # array([5., 5., 5., 5.]) np.sum(nd4,axis=-1) # array([4., 4., 4., 4., 4.])
nd5 = np.ones(shape=(5,4,3))
nd5
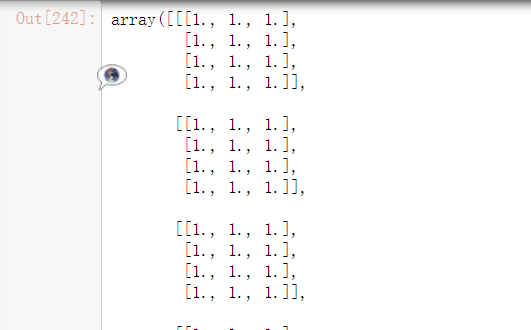
nd5.sum(axis=-1)

求4维矩阵中最后两维的和
nd6 = np.ones(shape=(6,5,4,3)) nd6 nd6.sum(-1).sum(-1) # array([[12., 12., 12., 12., 12.], [12., 12., 12., 12., 12.], [12., 12., 12., 12., 12.], [12., 12., 12., 12., 12.], [12., 12., 12., 12., 12.], [12., 12., 12., 12., 12.]]) #sum中的值可以是int tuple nd6.sum((-1,-2)) # array([[12., 12., 12., 12., 12.], [12., 12., 12., 12., 12.], [12., 12., 12., 12., 12.], [12., 12., 12., 12., 12.], [12., 12., 12., 12., 12.], [12., 12., 12., 12., 12.]])
最大最小值:nd.max/ nd.min
nd7 = np.random.randint(0,100,size=(5,4)) nd7 # array([[86, 88, 26, 21], [30, 94, 47, 9], [ 9, 54, 30, 74], [ 9, 57, 45, 61], [89, 16, 36, 28]]) nd7.max() # 94 nd7.max(axis=0) # array([89, 94, 47, 74]) nd7.min(axis=1) # array([21, 9, 9, 9, 16])
平均值:nd.mean()
nd7.mean() # 45.45 nd7.mean(axis=0) # array([44.6, 61.8, 36.8, 38.6]) nd7.mean(axis=1) # array([55.25, 45. , 41.75, 43. , 42.25])
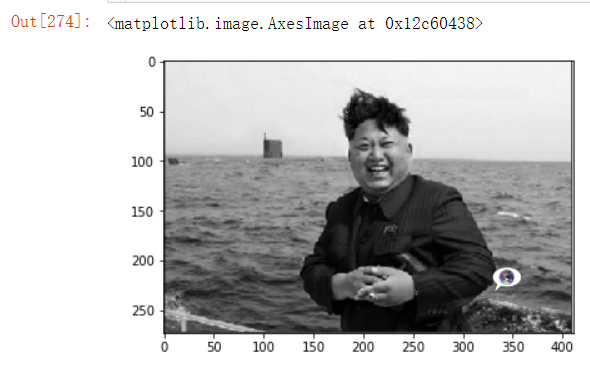
案例:将图片黑白(灰度化处理)
plt.imshow(sanpang) sp = (sanpang * 255).astype(np.uint8) plt.imshow(sp.max(axis=-1),cmap='gray')

plt.imshow(sp.min(axis=-1),cmap='gray')
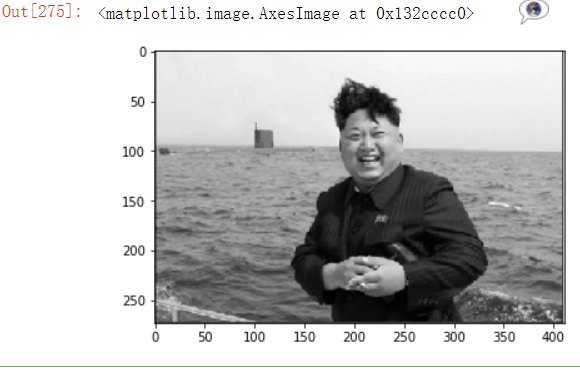
plt.imshow(sp.mean(axis=-1),cmap='gray')
其他聚合操作
Function Name NaN-safe Version Description
np.sum np.nansum Compute sum of elements
np.prod np.nanprod Compute product of elements
np.mean np.nanmean Compute mean of elements
np.std np.nanstd Compute standard deviation
np.var np.nanvar Compute variance
np.min np.nanmin Find minimum value
np.max np.nanmax Find maximum value
np.argmin np.nanargmin Find index of minimum value 找到最小数的下标
np.argmax np.nanargmax Find index of maximum value 找到最大数的下标
np.median np.nanmedian Compute median of elements
np.percentile np.nanpercentile Compute rank-based statistics of elements
np.any N/A Evaluate whether any elements are true
np.all N/A Evaluate whether all elements are true
np.power 幂运算
np.argwhere(nd1<0)
n = np.array([[1,2,3],[np.NaN,2,3]]) n # array([[ 1., 2., 3.], [nan, 2., 3.]]) #任何数值+NaN返回的都是NaN n.sum() # nan #带有nan的函数都会将nan视为0 np.nansum(n) # 11.0
argmax/argmin/argwhere
nd9 = np.random.randint(0,150,size=(10,8))
nd9

nd9.ravel()

#找到最大值的下标,argmax在查找最大值的时候,会默认将数组扁平化 nd9.ravel()[[np.argmax(nd9.ravel())]] # array([148]) nd9.ravel()[np.argwhere(nd9.ravel()<100).ravel()] #能不写变量的地方尽量不谢,因为变量一旦定义,就需要消耗内存空间,垃圾回收需要多处理一些垃圾变量 # array([12, 55, 89, 46, 48, 30, 2, 7, 4, 30, 15, 95, 26, 59, 68, 95, 47, 64, 15, 36, 75, 21, 29, 98, 93, 71, 60, 83, 34, 56, 16, 19, 86, 88, 4, 94, 80, 96, 2, 26, 69, 82, 14, 97, 89, 85, 94, 55, 90, 4, 54])
轴移动
moveaxis 可以将数组的轴移动到新的位置。其方法如下:
numpy.moveaxis(a, source, destination) 其中:
a:数组。source:要移动的轴的原始位置。destination:要移动的轴的目标位置。
nd10 = np.random.randint(0,10,size=(5,4)) nd10 # array([[0, 6, 3, 7], [5, 6, 5, 8], [0, 2, 5, 1], [0, 8, 9, 1], [9, 5, 0, 7]]) #转置 nd10.T # array([[0, 5, 0, 0, 9], [6, 6, 2, 8, 5], [3, 5, 5, 9, 0], [7, 8, 1, 1, 7]]) np.moveaxis(nd10,0,1) # array([[0, 5, 0, 0, 9], [6, 6, 2, 8, 5], [3, 5, 5, 9, 0], [7, 8, 1, 1, 7]]) nd11 = np.random.randint(0,10,size=(3,3,3)) nd11 # array([[[7, 1, 2], [3, 7, 7], [3, 1, 5]], [[0, 0, 4], [0, 8, 7], [9, 4, 7]], [[0, 2, 8], [2, 3, 9], [5, 2, 3]]]) nd11.T # array([[[7, 0, 0], [3, 0, 2], [3, 9, 5]], [[1, 0, 2], [7, 8, 3], [1, 4, 2]], [[2, 4, 8], [7, 7, 9], [5, 7, 3]]]) np.moveaxis(np.moveaxis(nd11,0,-1),0,1) #y x z #z x y #x z y # array([[[7, 0, 0], [3, 0, 2], [3, 9, 5]], [[1, 0, 2], [7, 8, 3], [1, 4, 2]], [[2, 4, 8], [7, 7, 9], [5, 7, 3]]])
轴交换
和 moveaxis 不同的是,swapaxes 可以用来交换数组的轴。其方法如下:
numpy.swapaxes(a, axis1, axis2) 其中:
a:数组。axis1:需要交换的轴 1 位置。axis2:需要与轴 1 交换位置的轴 1 位置。
举个例子:
nd11.T # array([[[7, 0, 0], [3, 0, 2], [3, 9, 5]], [[1, 0, 2], [7, 8, 3], [1, 4, 2]], [[2, 4, 8], [7, 7, 9], [5, 7, 3]]]) np.swapaxes(nd11,0,-1) # array([[[7, 0, 0], [3, 0, 2], [3, 9, 5]], [[1, 0, 2], [7, 8, 3], [1, 4, 2]], [[2, 4, 8], [7, 7, 9], [5, 7, 3]]]) nd12 = np.random.randint(0,10,size=(3,3,3,3)) nd12.T np.swapaxes(nd12,0,-1) np.moveaxis(np.moveaxis(np.moveaxis(nd12,0,-1),0,1),0,2)
数组转置
transpose 类似于矩阵的转置,它可以将 2 维数组的水平轴和垂直交换。其方法如下:
numpy.transpose(a, axes=None) 其中:
a:数组。axis:该值默认为none,表示转置。如果有值,那么则按照值替换轴。
nd11.transpose() # array([[[7, 0, 0], [3, 0, 2], [3, 9, 5]], [[1, 0, 2], [7, 8, 3], [1, 4, 2]], [[2, 4, 8], [7, 7, 9], [5, 7, 3]]])
数组'循环'
数组元素的循环
1.20.1 tile 与 repeat
list_ = [1,2,3]*3 list_ # [1, 2, 3, 1, 2, 3, 1, 2, 3] nd13 = np.random.randint(0,10,3) nd13 # array([18, 12, 24]) np.tile(nd13,3) # array([6, 4, 8, 6, 4, 8, 6, 4, 8]) np.repeat(nd13,3) # array([6, 6, 6, 4, 4, 4, 8, 8, 8]) nd14 = np.random.randint(0,10,(5,4)) nd14 # array([[8, 0, 9, 3], [6, 0, 5, 0], [5, 2, 7, 6], [6, 5, 0, 9], [6, 0, 9, 2]]) np.repeat(nd14,3,axis=1) # array([[8, 8, 8, 0, 0, 0, 9, 9, 9, 3, 3, 3], [6, 6, 6, 0, 0, 0, 5, 5, 5, 0, 0, 0], [5, 5, 5, 2, 2, 2, 7, 7, 7, 6, 6, 6], [6, 6, 6, 5, 5, 5, 0, 0, 0, 9, 9, 9], [6, 6, 6, 0, 0, 0, 9, 9, 9, 2, 2, 2]])
ndarray的矩阵操作
1.21.1 1. 基本矩阵操作
1) 算术运算符:
- 加减乘除
nd15 = np.random.randint(10,100,size=(5,4)) nd16 = np.random.randint(1,10,size=(5,4)) display(nd15,nd16) # array([[11, 75, 42, 82], [24, 75, 26, 87], [21, 36, 14, 88], [90, 68, 37, 28], [77, 25, 37, 95]]) # array([[3, 5, 1, 7], [3, 1, 8, 7], [9, 7, 4, 3], [2, 7, 4, 4], [1, 8, 5, 6]])
nd15 + nd16 # array([[ 8, 70, 41, 75], [21, 74, 18, 80], [12, 29, 10, 85], [88, 61, 33, 24], [76, 17, 32, 89]]) nd15 * nd16 # array([[ 33, 375, 42, 574], [ 72, 75, 208, 609], [189, 252, 56, 264], [180, 476, 148, 112], [ 77, 200, 185, 570]]) nd15 / nd16 # array([[ 3.66666667, 15. , 42. , 11.71428571], [ 8. , 75. , 3.25 , 12.42857143], [ 2.33333333, 5.14285714, 3.5 , 29.33333333], [45. , 9.71428571, 9.25 , 7. ], [77. , 3.125 , 7.4 , 15.83333333]])
np.add() 求和
不对原来的数组产生影响
np.add(nd15,nd16) # array([[ 14, 80, 43, 89], [ 27, 76, 34, 94], [ 30, 43, 18, 91], [ 92, 75, 41, 32], [ 78, 33, 42, 101]])
乘积 np.multiply() 乘积
不对原来的结果产生影响
np.multiply(nd15,nd16) # array([[ 33, 375, 42, 574], [ 72, 75, 208, 609], [189, 252, 56, 264], [180, 476, 148, 112], [ 77, 200, 185, 570]])
矩阵的乘积 np.dot()
display(nd15,nd16) # array([[11, 75, 42, 82], [24, 75, 26, 87], [21, 36, 14, 88], [90, 68, 37, 28], [77, 25, 37, 95]]) # array([[3, 5, 1, 7], [3, 1, 8, 7], [9, 7, 4, 3], [2, 7, 4, 4], [1, 8, 5, 6]]) np.dot(nd15,nd16.T) # array([[1024, 1018, 1038, 1043, 1313], [1082, 964, 1106, 1025, 1276], [ 873, 827, 761, 702, 907], [ 843, 830, 1518, 916, 987], [1058, 1217, 1301, 857, 1032]]) nd17 = np.random.randint(0,100,size=(5,4,3)) # array([[[26, 36, 24], [83, 36, 56], [50, 12, 43], [30, 1, 19]], [[59, 79, 87], [49, 87, 81], [51, 43, 93], [93, 8, 49]], .... nd17 * 0 #标量 array([[[0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 0]], [[0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 0]], [[0, 0, 0], [0, 0, 0],
三维乘以一维
nd18 = np.random.randint(0,10,size=3) nd18 # array([0, 3, 1]) np.dot(nd17,nd18) # array([[132, 164, 79, 22], [324, 342, 222, 73], [239, 318, 315, 322], [219, 144, 144, 297], [246, 105, 115, 186]])
三维乘以二维
相邻两维数据相乘会出现错误
nd19 = np.random.randint(0,10,size=(3,4))
np.dot(nd17,nd19)
广播机制
【重要】ndarray广播机制的两条规则
规则一:为缺失的维度补1
规则二:假定缺失元素用已有值填充
例1: m = np.ones((2, 3)) a = np.arange(3) 求m+a
nd18 + 3 # array([3, 6, 4])
ndarray的排序
小测验: 使用以上所学numpy的知识,对一个ndarray对象进行选择排序。
代码越短越好
冒泡排序
res = np.random.randint(0,10,(5,2)).reshape(-1) res # array([4, 3, 0, 0, 8, 0, 8, 0, 4, 8]) num = 0 for i in range(res.size-1): for j in range(res.size-i-1): if res[j] > res[j+1]: res[j],res[j+1] = res[j+1],res[j] num+=1 result = np.random.randint(0,10,(5,2)).reshape(-1) result # array([8, 6, 3, 1, 5, 5, 1, 2, 4, 8])
一个循环搞定排序
#一个循环搞定排序 argmin argmax def sort_nd(nd): for i in range(nd.size): min_index = nd[i:].argmin()+ i nd[i],nd[min_index] = nd[min_index],nd[i] sort_nd(result) result
# array([1, 1, 2, 3, 4, 5, 5, 6, 8, 8])
'快速'排序
np.sort()与ndarray.sort()都可以,但有区别:
- np.sort()不改变输入
- ndarray.sort()本地处理,不占用空间,但改变输入
res_ = np.random.randint(0,10,size=10) res_ # array([3, 3, 0, 3, 5, 4, 0, 2, 7, 2]) np.sort(res_)[::-1] array([7, 5, 4, 3, 3, 3, 2, 2, 0, 0])
部分排序
`python np.partition(a,k)
有的时候我们不是对全部数据感兴趣,我们可能只对最小或最大的一部分感兴趣。
- 当k为正时,我们想要得到最小的k个数
- 当k为负时,我们想要得到最大的k个数
res_1 = np.random.randint(0,10000,size=100) res_1 # array([1709, 2665, 3007, 3526, 3646, 864, 9796, 148, 8290, 505, 9249, 6741, 8795, 7064, 5812, 5241, 9618, 3818, 6721, 1333, 7715, 2093, 4247, 8537, 1161, 6773, 2475, 6879, 4275, 9834, 1403, 4711, 9187, 9607, 7247, 797, 8479, 149, 8054, 445, 3059, 6399, 9792, 1711, 4836, 4363, 7772, 7030, 1791, 6757, 2366, 5251, 6828, 5969, 7670, 1450, 5393, 6859, 3347, 2385, 3326, 2409, 2554, 8362, 1114, 5436, 399, 4108, 5116, 4582, 2345, 3580, 5788, 3676, 7640, 7906, 644, 62, 1050, 7893, 7372, 8485, 5739, 9402, 6608, 6070, 8869, 6203, 1471, 7006, 7344, 1466, 1788, 5421, 6811, 7126, 3724, 9810, 510, 2374]) np.partition(res_1,-5) # array([ 148, 62, 149, 399, 445, 505, 510, 644, 797, 864, 1050, 1114, 1161, 1333, 1403, 1450, 1466, 1471, 1709, 1711, 1788, 1791, 2093, 2345, 2366, 2374, 2385, 2409, 2475, 2554, 2665, 3007, 3059, 3326, 3347, 3526, 3580, 3646, 3676, 3724, 3818, 4108, 4247, 4275, 4363, 4582, 4711, 4836, 5116, 5241, 5393, 5251, 5421, 5436, 5739, 5788, 5812, 5969, 6070, 6203, 6399, 6608, 6721, 6741, 6757, 6773, 6811, 6828, 6859, 6879, 7006, 7030, 7064, 7126, 7247, 7372, 7344, 7640, 7670, 7715, 7772, 7893, 7906, 8054, 8290, 8362, 8479, 8485, 8795, 8537, 8869, 9187, 9249, 9402, 9607, 9618, 9792, 9796, 9810, 9834]) np.partition(res_1,4) # array([ 148, 62, 149, 399, 445, 505, 510, 644, 797, 864, 1050, 1114, 1161, 1333, 1403, 1450, 1466, 1471, 1709, 1711, 1788, 1791, 2093, 2345, 2366, 2374, 2385, 2409, 2475, 2554, 2665, 3007, 3059, 3326, 3347, 3526, 3580, 3646, 3676, 3724, 3818, 4108, 4247, 4275, 4363, 4582, 4711, 4836, 5116, 5241, 5251, 5393, 5421, 5436, 5739, 5788, 5812, 5969, 6070, 6203, 6399, 6608, 6721, 6741, 6757, 6773, 6811, 6828, 6859, 6879, 7006, 7030, 7064, 7126, 7247, 7344, 7372, 7640, 7670, 7715, 7772, 7893, 7906, 8054, 8290, 8362, 8479, 8485, 8537, 8795, 8869, 9187, 9249, 9402, 9607, 9618, 9792, 9796, 9810, 9834]) np.sort(res_1)[::-1][:5] # array([9834, 9810, 9796, 9792, 9618])


