C. New Year Book Reading

New Year is coming, and Jaehyun decided to read many books during 2015, unlike this year. He has n books numbered by integers from 1 to n. The weight of the i-th (1 ≤ i ≤ n) book is wi.

As Jaehyun's house is not large enough to have a bookshelf, he keeps the n books by stacking them vertically. When he wants to read a certain book x, he follows the steps described below.

1. He lifts all the books above book x.
2. He pushes book x out of the stack.
3. He puts down the lifted books without changing their order.
4. After reading book x, he puts book x on the top of the stack.

He decided to read books for m days. In the j-th (1 ≤ j ≤ m) day, he will read the book that is numbered with integer bj (1 ≤ bj ≤ n). To read the book, he has to use the process described in the paragraph above. It is possible that he decides to re-read the same book several times.

After making this plan, he realized that the total weight of books he should lift during m days would be too heavy. So, he decided to change the order of the stacked books before the New Year comes, and minimize the total weight. You may assume that books can be stacked in any possible order. Note that book that he is going to read on certain step isn't considered as lifted on that step. Can you help him?

Input

The first line contains two space-separated integers n (2 ≤ n ≤ 500) and m (1 ≤ m ≤ 1000) — the number of books, and the number of days for which Jaehyun would read books.

The second line contains n space-separated integers w1, w2, ..., wn (1 ≤ wi ≤ 100) — the weight of each book.

The third line contains m space separated integers b1, b2, ..., bm (1 ≤ bj ≤ n) — the order of books that he would read. Note that he can read the same book more than once.

Output

Print the minimum total weight of books he should lift, which can be achieved by rearranging the order of stacked books.

Sample test(s)

input

3 5
1 2 3
1 3 2 3 1

output

12

Note

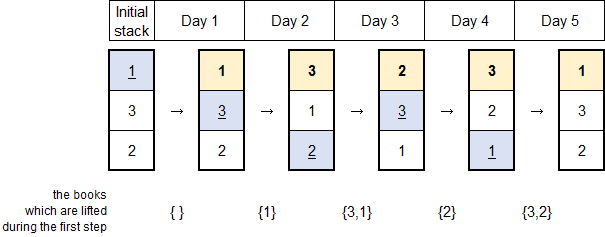
Here's a picture depicting the example. Each vertical column presents the stacked books.

这道题的主要是考虑怎么排序，其实只要按照取书本的顺序就行了，比如1 1 1 1 1 1 2，取两本书2 1，那么显然初始序列是1 2 时总价值最小，分析样例，如果3本书取书的顺序是3 1 2 ，那么这些步骤后书的排序顺序一定是2 3 1，但是初始序列是3 1 2的总价值最小，那么加上后面的也一定最小。 #include<stdio.h>
#include<string.h>
int w[600],a[600],c[1005];
int main()
{
int n,m,i,j,t,flag,sum,u,h;
while(scanf("%d%d",&n,&m)!=EOF)
{
memset(w,0,sizeof(w));
memset(a,0,sizeof(a));
memset(c,0,sizeof(c));
for(i=1;i<=n;i++){
scanf("%d",&w[i]);
}
t=0;
for(i=1;i<=m;i++){
scanf("%d",&c[i]);
if(t==0){
t++;a[t]=c[i];continue;
}
flag=1;
for(j=1;j<=t;j++){
if(c[i]==a[j]){
flag=0;break;
}
}
if(flag==0)continue;
else{
t++;a[t]=c[i];continue;
}
}
sum=0;
for(i=1;i<=m;i++){
/*for(j=1;j<=n;j++){
printf("%d ",a[j]);
}printf("\n");*/

if(c[i]==a[1])continue;
for(j=1;j<=t;j++){
if(c[i]==a[j]){
u=j;break;
}
sum=sum+w[a[j]];
}
h=a[u];
for(j=u;j>=2;j--){
a[j]=a[j-1];
}
a[1]=h;
}
printf("%d\n",sum);
}
return 0;
}