B. OR in Matrix

Let's define logical OR as an operation on two logical values (i. e. values that belong to the set {0, 1}) that is equal to 1 if either or both of the logical values is set to 1, otherwise it is 0. We can define logical OR of three or more logical values in the same manner:

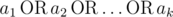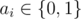 where  is equal to 1 if some ai = 1, otherwise it is equal to 0.

Nam has a matrix A consisting of m rows and n columns. The rows are numbered from 1 to m, columns are numbered from 1 to n. Element at row i (1 ≤ i ≤ m) and column j (1 ≤ j ≤ n) is denoted as Aij. All elements of A are either 0 or 1. From matrix A, Nam creates another matrix B of the same size using formula:

.

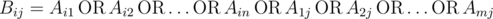(Bij is OR of all elements in row i and column j of matrix A)

Nam gives you matrix B and challenges you to guess matrix A. Although Nam is smart, he could probably make a mistake while calculating matrix B, since size of A can be large.

Input

The first line contains two integer m and n (1 ≤ m, n ≤ 100), number of rows and number of columns of matrices respectively.

The next m lines each contain n integers separated by spaces describing rows of matrix B (each element of B is either 0 or 1).

Output

In the first line, print "NO" if Nam has made a mistake when calculating B, otherwise print "YES". If the first line is "YES", then also print mrows consisting of n integers representing matrix A that can produce given matrix B. If there are several solutions print any one.

Sample test(s)

input

2 2
1 0
0 0

output

NO

input

2 3
1 1 1
1 1 1

output

YES
1 1 1
1 1 1

input

2 3
0 1 0
1 1 1

output

YES
0 0 0
0 1 0

这题刚开始以为要用搜索，看了别人的题解才知道不用的，因为只要把0所在的行和列都变成0，其他的都变为1就得到了原来的矩阵A,（注意：其实由B得到的矩阵不止A这一个，但是这样得到的A是所有的到矩阵的最优解，因为得到1的数是最多的。

#include<stdio.h>
#include<string.h>
int a[200][200],b[200][200],c[200][200];
int main()
{
	int n,m,i,j,h,t,flag,flag1;
	while(scanf("%d%d",&n,&m)!=EOF)
	{
		memset(a,0,sizeof(a));
		memset(b,0,sizeof(b));
		memset(c,0,sizeof(c));
		for(i=1;i<=n;i++){
			for(j=1;j<=m;j++){
				scanf("%d",&a[i][j]);
				b[i][j]=1;
			}
		}
		for(i=1;i<=n;i++){
			for(j=1;j<=m;j++){
				if(a[i][j]==0){
					for(h=1;h<=m;h++){
						b[i][h]=0;
					}
					for(t=1;t<=n;t++){
						b[t][j]=0;
					}
				}
			}
		}
		
		for(i=1;i<=n;i++){
			for(j=1;j<=m;j++){
				flag=0;
				for(h=1;h<=m;h++){
					if(b[i][h]==1){
						flag=1;break;
					}
				}
				for(t=1;t<=n;t++){
					if(b[t][j]==1){
						flag=1;break;
					}
				}
				if(flag==1){
					c[i][j]=1;continue;
				}
				c[i][j]=0;
			}
		}
		flag1=1;
		for(i=1;i<=n;i++){
			for(j=1;j<=m;j++){
				if(c[i][j]!=a[i][j]){
					flag1=0;break;
				}
			}
			if(flag1==0)break;
		}
		if(flag1==0){
			printf("NO\n");continue;
		}
		printf("YES\n");
		for(i=1;i<=n;i++){
			for(j=1;j<=m;j++){
				if(j!=m)printf("%d ",b[i][j]);
				else printf("%d\n",b[i][j]);
			}
		}
	}
	return 0;
}