Codeforces Round #312 (Div. 2) C. Amr and Chemistry

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Amr loves Chemistry, and specially doing experiments. He is preparing for a new interesting experiment.

Amr has n different types of chemicals. Each chemical i has an initial volume of ai liters. For this experiment, Amr has to mix all the chemicals together, but all the chemicals volumes must be equal first. So his task is to make all the chemicals volumes equal.

To do this, Amr can do two different kind of operations.

• Choose some chemical i and double its current volume so the new volume will be 2ai
• Choose some chemical i and divide its volume by two (integer division) so the new volume will be 

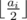
Suppose that each chemical is contained in a vessel of infinite volume. Now Amr wonders what is the minimum number of operations required to make all the chemicals volumes equal?

Input

The first line contains one number n (1 ≤ n ≤ 105), the number of chemicals.

The second line contains n space separated integers ai (1 ≤ ai ≤ 105), representing the initial volume of the i-th chemical in liters.

Output

Output one integer the minimum number of operations required to make all the chemicals volumes equal.

Sample test(s)

input

3
4 8 2

output

2

input

3
3 5 6

output

5

Note

In the first sample test, the optimal solution is to divide the second chemical volume by two, and multiply the third chemical volume by two to make all the volumes equal 4.

In the second sample test, the optimal solution is to divide the first chemical volume by two, and divide the second and the third chemical volumes by two twice to make all the volumes equal 1.

这题可以用二进制做，比赛的时候没有做出，可以开一个结构体vis[i],记录num（表示有多少个数能通过*2或/2得到i）和minmum（表示所有能通过*2或/2得到i的最小步数），然后对于每一个读入的值，计算它能够变成的数。具体如下：

1.先一直右移到小于等于100000的数，每次移动一位判断。

2.重新左移，如果碰到末位数是1，但本身不等于1，那么要先处理一下，即把这个数的末位变为0，然后一直右移到小于等于100000的数。

#include<stdio.h>
#include<string.h>
#define inf 88888888
#define maxn 100060
int a[maxn];
struct node{
	int minmum,num;
}vis[maxn];
void deal(int x)
{
	int n,m,i,j,wei=0,bushu,t,y;
	n=x;bushu=0;
	while(n<=100000){
		vis[n].num++;
		vis[n].minmum+=bushu;
		bushu++;
		n*=2;
	}
	n=x;bushu=0;
	while(n>0){
		if(x!=n){
			vis[n].num++;
		    vis[n].minmum+=bushu;
		}
		if(n%2==1 && n!=1){
			t=bushu+2;
			y=n/2*2;
			while(y<=100000){
				vis[y].num++;
				vis[y].minmum+=t;
				t++;
				y*=2;
			}
		}
		bushu++;
		n/=2;
	}
}


int main()
{
	int n,m,i,j,num;
	while(scanf("%d",&n)!=EOF)
	{
		memset(vis,0,sizeof(vis));
		for(i=1;i<=n;i++){
			scanf("%d",&a[i]);
			deal(a[i]);
		}
		num=inf;
		for(i=1;i<=100000;i++){
			if(vis[i].num==n){
				if(vis[i].minmum<num){
					num=vis[i].minmum;
				}
			}
		}
		printf("%d\n",num);
	}
	return 0;
}