hdu5531 Rebuild
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 181 Accepted Submission(s): 42
Total Submission(s): 181 Accepted Submission(s): 42
Problem Description
Archaeologists find ruins of Ancient ACM Civilization, and they want to rebuild it.
The ruins form a closed path on an x-y plane, which has n endpoints. The endpoints locate on (x1,y1), (x2,y2), …,(xn,yn) respectively. Endpoint i and endpointi−1 are adjacent for 1<i≤n, also endpoint 1 and endpoint n are adjacent. Distances between any two adjacent endpoints are positive integers.
To rebuild, they need to build one cylindrical pillar at each endpoint, the radius of the pillar of endpoint i is ri. All the pillars perpendicular to the x-y plane, and the corresponding endpoint is on the centerline of it. We call two pillars are adjacent if and only if two corresponding endpoints are adjacent. For any two adjacent pillars, one must be tangent externally to another, otherwise it will violate the aesthetics of Ancient ACM Civilization. If two pillars are not adjacent, then there are no constraints, even if they overlap each other.
Note that ri must not be less than 0 since we cannot build a pillar with negative radius and pillars with zero radius are acceptable since those kind of pillars still exist in their neighbors.
You are given the coordinates of n endpoints. Your task is to find r1,r2,…,rn which makes sum of base area of all pillars as minimum as possible.
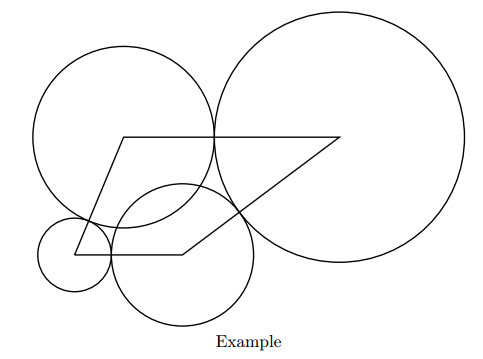
For example, if the endpoints are at (0,0), (11,0), (27,12), (5,12), we can choose (r1, r2, r3, r4)=(3.75, 7.25, 12.75, 9.25). The sum of base area equals to 3.752π+7.252π+12.752π+9.252π=988.816…. Note that we count the area of the overlapping parts multiple times.
If there are several possible to produce the minimum sum of base area, you may output any of them.
The ruins form a closed path on an x-y plane, which has n endpoints. The endpoints locate on (x1,y1), (x2,y2), …,(xn,yn) respectively. Endpoint i and endpointi−1 are adjacent for 1<i≤n, also endpoint 1 and endpoint n are adjacent. Distances between any two adjacent endpoints are positive integers.
To rebuild, they need to build one cylindrical pillar at each endpoint, the radius of the pillar of endpoint i is ri. All the pillars perpendicular to the x-y plane, and the corresponding endpoint is on the centerline of it. We call two pillars are adjacent if and only if two corresponding endpoints are adjacent. For any two adjacent pillars, one must be tangent externally to another, otherwise it will violate the aesthetics of Ancient ACM Civilization. If two pillars are not adjacent, then there are no constraints, even if they overlap each other.
Note that ri must not be less than 0 since we cannot build a pillar with negative radius and pillars with zero radius are acceptable since those kind of pillars still exist in their neighbors.
You are given the coordinates of n endpoints. Your task is to find r1,r2,…,rn which makes sum of base area of all pillars as minimum as possible.

For example, if the endpoints are at (0,0), (11,0), (27,12), (5,12), we can choose (r1, r2, r3, r4)=(3.75, 7.25, 12.75, 9.25). The sum of base area equals to 3.752π+7.252π+12.752π+9.252π=988.816…. Note that we count the area of the overlapping parts multiple times.
If there are several possible to produce the minimum sum of base area, you may output any of them.
Input
The first line contains an integer t indicating
the total number of test cases. The following lines describe a test case.
The first line of each case contains one positive integer n, the size of the closed path. Next n lines, each line consists of two integers (xi,yi) indicate the coordinate of the i-th endpoint.
1≤t≤100
3≤n≤104
|xi|,|yi|≤104
Distances between any two adjacent endpoints are positive integers.
The first line of each case contains one positive integer n, the size of the closed path. Next n lines, each line consists of two integers (xi,yi) indicate the coordinate of the i-th endpoint.
1≤t≤100
3≤n≤104
|xi|,|yi|≤104
Distances between any two adjacent endpoints are positive integers.
Output
If such answer doesn't exist, then print on a single line "IMPOSSIBLE" (without the quotes). Otherwise, in the first line print the minimum sum of base area, and then print n lines,
the i-th
of them should contain a number ri,
rounded to 2 digits after the decimal point.
If there are several possible ways to produce the minimum sum of base area, you may output any of them.
If there are several possible ways to produce the minimum sum of base area, you may output any of them.
Sample Input
3
4
0 0
11 0
27 12
5 12
5
0 0
7 0
7 3
3 6
0 6
5
0 0
1 0
6 12
3 16
0 12
Sample Output
988.82
3.75
7.25
12.75
9.25
157.08
6.00
1.00
2.00
3.00
0.00
IMPOSSIBLE
这题卡了很久了,有点麻烦的题。给你一个多边形,问你能不能构造出圆心在多边形的顶点且各个圆相切,如果能,则求出所有圆的最大面积和。要分奇数和偶数讨论,奇数当一个圆的半径改变时,第一个圆和最后一个圆距离会变,偶数则不变。
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<iostream>
#include<stdlib.h>
#include<set>
#include<map>
#include<queue>
#include<vector>
#include<bitset>
#pragma comment(linker, "/STACK:1024000000,1024000000")
template <class T>
bool scanff(T &ret){ //Faster Input
char c; int sgn; T bit=0.1;
if(c=getchar(),c==EOF) return 0;
while(c!='-'&&c!='.'&&(c<'0'||c>'9')) c=getchar();
sgn=(c=='-')?-1:1;
ret=(c=='-')?0:(c-'0');
while(c=getchar(),c>='0'&&c<='9') ret=ret*10+(c-'0');
if(c==' '||c=='\n'){ ret*=sgn; return 1; }
while(c=getchar(),c>='0'&&c<='9') ret+=(c-'0')*bit,bit/=10;
ret*=sgn;
return 1;
}
#define inf 1073741823
#define llinf 4611686018427387903LL
#define PI acos(-1.0)
#define lth (th<<1)
#define rth (th<<1|1)
#define rep(i,a,b) for(int i=int(a);i<=int(b);i++)
#define drep(i,a,b) for(int i=int(a);i>=int(b);i--)
#define gson(i,root) for(int i=ptx[root];~i;i=ed[i].next)
#define tdata int testnum;scanff(testnum);for(int cas=1;cas<=testnum;cas++)
#define mem(x,val) memset(x,val,sizeof(x))
#define mkp(a,b) make_pair(a,b)
#define findx(x) lower_bound(b+1,b+1+bn,x)-b
#define pb(x) push_back(x)
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
#define NN 100100
struct node{
double x,y;
}a[NN];
int n;
double len[NN];
double r[NN];
double caldis(int x,int y){
return sqrt((a[x].x-a[y].x)*(a[x].x-a[y].x)+(a[x].y-a[y].y)*(a[x].y-a[y].y));
}
double cal(int idx,double lx){
double temp=lx;
double s=0.0;
rep(i,1,n){
s+=lx*lx;
r[idx]=lx;
if(lx<0.0||lx>len[idx]||lx>len[idx==1?n:idx-1])return -1.0;
lx=len[idx]-lx;
idx++;
if(idx>n)idx=1;
}
if(fabs(temp-lx)>1e-7)return -1.0;
return s;
}
int main(){
tdata{
scanff(n);
rep(i,1,n){
scanf("%lf%lf",&a[i].x,&a[i].y);
}
rep(i,1,n){
if(i!=n)len[i]=caldis(i,i+1);
else len[i]=caldis(i,1);
}
int idx;
if(n&1){
double lenx=0.0;
idx=1;
rep(i,1,n){
if(i&1)lenx+=len[idx];
else lenx-=len[idx];
idx++;
if(idx>n)idx=1;
}
lenx/=2.0;
double ans=cal(1,lenx);
if(ans>=0.0){
printf("%.2f\n",ans*PI);
rep(i,1,n){
printf("%.2f\n",r[i]);
}
}
else printf("IMPOSSIBLE\n");
}
else{
double lx=0.0,rx=len[1],t=0.0;
idx=1;
rep(i,1,n){
t=len[idx]-t;
if(i&1)rx=min(rx,t);
else lx=max(lx,-t);
idx++;
if(idx>n)idx=1;
}
if(lx>rx){
printf("IMPOSSIBLE\n");
continue;
}
rep(i,1,250){
/*
double d=(rx-lx)/3.0;
double d1=lx+d;
double d2=rx-d;
*/
double d1=(lx*2+rx)/3.0;
double d2=(lx+rx*2)/3.0;
if(cal(1,d1)<cal(1,d2))rx=d2;
else lx=d1;
}
double ans=cal(1,lx);
if(ans<0.0){
printf("IMPOSSIBLE\n");
continue;
}
printf("%.2f\n",ans*PI);
rep(i,1,n){
printf("%.2f\n",r[i]);
}
}
}
return 0;
}