P3366 【模板】最小生成树

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出orz

输入输出格式

输入格式：

第一行包含两个整数N、M，表示该图共有N个结点和M条无向边。（N<=5000，M<=200000）

接下来M行每行包含三个整数Xi、Yi、Zi，表示有一条长度为Zi的无向边连接结点Xi、Yi

输出格式：

输出包含一个数，即最小生成树的各边的长度之和；如果该图不连通则输出orz

输入输出样例

输入样例#1： 复制

4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

输出样例#1： 复制

7

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=20

对于40%的数据：N<=50，M<=2500

对于70%的数据：N<=500，M<=10000

对于100%的数据：N<=5000，M<=200000

样例解释：

 

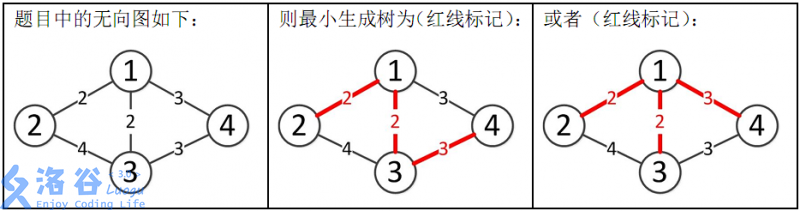
所以最小生成树的总边权为2+2+3=7

思路：

这道题用最小生成树来做，Prim算法我不是很熟悉，所以我来讲讲Kruskal算法。

Kruskal算法也就是并查集做法，算法思路：

1. 将图中的所有边都去掉。
2. 将边按权值从小到大的顺序添加到图中，保证添加的过程中不会形成环
3. 重复上一步直到连接所有顶点，此时就生成了最小生成树。这是一种贪心策略。

这道题就是这样的思路，在注释中也会有所体现。

 

源代码：

#include<bits/stdc++.h>
using namespace std;
int n,m;
struct node{
    int u;
    int w;
    int v;
}g[200010];
bool cmp(node a,node b){
    return a.w<b.w;
}//排序函数
int fa[10010];
void init(){
    for(int i=1;i<=n;i++){
        fa[i]=i;
    }
}//初始化
int get(int x){
    if(fa[x]==x){
        return x;
    }else{
        int y=get(fa[x]);
        fa[x]=y;
        return y;
    }
}//找根
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        cin>>g[i].u>>g[i].v>>g[i].w;
    }//输入
    init();
    sort(g+1,g+1+m,cmp);//排序，为后面的贪心思想做准备
    int cnt=0;
    for(int i=1;i<=m;i++){
        int x=get(g[i].u),y=get(g[i].v);
        if(x!=y){
            cnt+=g[i].w;
            fa[x]=y;//因为进行了排序，所以现在找到的就是最小的，加到cnt上就行了
        }
    }

    cout<<cnt;
    return 0;
}