图论之最短路算法之SPFA算法
SPFA(Shortest Path Faster Algorithm)算法,是一种求最短路的算法。
SPFA的思路及写法和BFS有相同的地方,我就举一道例题(洛谷——P3371 【模板】单源最短路径(弱化版)来做讲解吧!
如题:
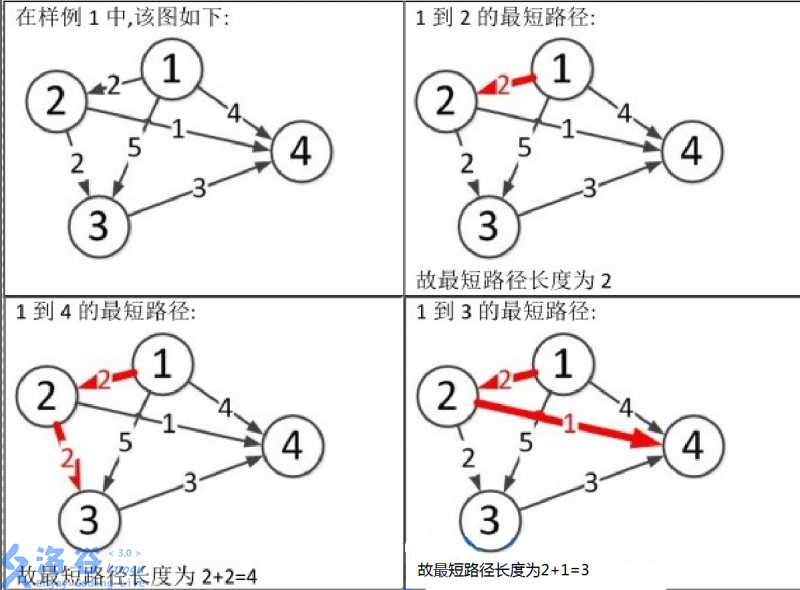
首先,我们先来定义一波变量吧:
struct node{
int v,w;
node (){ }
node (int _v,int _w){
v=_v;
w=_w;
}//构造函数
};
queue<int>qu;//必备队列
const int inf=0x3f3f3f3f;//最大值
vector<node> g[10010];//动态数组存点集
int inq[10010],dst[10010];//标记数组以及确认的最短路经
int n,m;
然后再来一个存图函数
void add(int u,int v,int w){
g[u].push_back(node(v,w));
}
好了,基本的变量函数已经准备好了,现在就开始我们的SPFA。
但需要传什么参数进去呢?那就简洁点,就只要一个s(松弛的点)
void spfa(){
}
首先我们来给dst赋一个最大值,因为求最短路嘛,当然要赋一个最大值嘛。
memset(dst,inf,sizeof dst);
然后就标记+dst还原成0+放进队列
int u=s;
dst[u]=0;
inq[u]=1;
qu.push(u);
下面就开始一波日常的操作:
while (!qu.empty()){
u=qu.front();
qu.pop();//弹出去,不然就出不去了(无限循环)
inq[u]=0;//取消标记,万一会重复走呢?
for (int i=0;i<g[u].size();i++){
int v=g[u][i].v;
int w=g[u][i].w;//取出来,简洁
if (dst[v]>dst[u]+w){
dst[v]=dst[u]+w;//如果松弛了更小,那就松弛吧
if (!inq[v]){
qu.push(v);
inq[v]=1;//如果没走过,那就放进qu在标记一下
}
}
}
}
main函数里就不用讲了嘛:
int main(){
int s;
cin>>n>>m>>s;
while (m--){
int u,v,w;
cin>>u>>v>>w;
add(u,v,w);
}
spfa(s);
for (int i=1;i<=n;i++){
if(dst[i]==0x3f3f3f3f){
cout<<2147483647<<" ";
}else{
cout<<dst[i]<<" ";
}
}
return 0;
}
最后,完整的代码为:
#include <bits/stdc++.h>
using namespace std;
struct node{
int v,w;
node (){ }
node (int _v,int _w){
v=_v;
w=_w;
}
};
queue<int>qu;
const int inf=0x3f3f3f3f;
vector<node> g[10010];
int inq[10010],dst[10010];
int n,m;
void add(int u,int v,int w){
g[u].push_back(node(v,w));
}
void spfa(int s){
memset(dst,inf,sizeof dst);
int u=s;
dst[u]=0;
inq[u]=1;
qu.push(u);
while (!qu.empty()){
u=qu.front();
qu.pop();
inq[u]=0;
for (int i=0;i<g[u].size();i++){
int v=g[u][i].v;
int w=g[u][i].w;
if (dst[v]>dst[u]+w){
dst[v]=dst[u]+w;
if (!inq[v]){
qu.push(v);
inq[v]=1;
}
}
}
}
}
int main(){
int s;
cin>>n>>m>>s;
while (m--){
int u,v,w;
cin>>u>>v>>w;
add(u,v,w);
}
spfa(s);
for (int i=1;i<=n;i++){
if(dst[i]==0x3f3f3f3f){
cout<<2147483647<<" ";
}else{
cout<<dst[i]<<" ";
}
}
return 0;
}
完美结束


