R-4 方差分析

本节内容：

1：方差分析的原理

2：单因数方差分析 、双因数分析

3：交互项

一：方差分析是原理

方差分析原理

对总体均值的假设检验，有三种情况：
1、总体均值与某个常数进行比较；
2、两个总体均值之间的比较；
3、两个以上总体均值之间的比较；

对于前两种情况，用Z分布和T分布就能快速得到假设检验结果。如果比较的总体大于三个，继续用它们也能够得到比较结果，只是需要两两比较，耗时耗力。

这种情况下，使用方差分析能够一次性比较两个及两个以上的总体均值，看看它们之间是否有显著性差异。

常用的方差分析方法包括：单因素方差分析、多因素方差分析、协方差分析、多元方差分析、重复测量方差分析、方差成分分析等。

分类为3种以上 ：采用方差分析判断显著性
原假设就是：X1 = X2 = X3 之间无显著性

二、单因数方差分析 、双因数分析

2.1 单因数方差分析

cre = read.csv("creditcard_exp.csv",stringsAsFactors = F)
cre  = na.omit(cre)

cre$edu = as.factor(cre$edu_class)
boxplot(avg_exp～edu_class,data=cre)
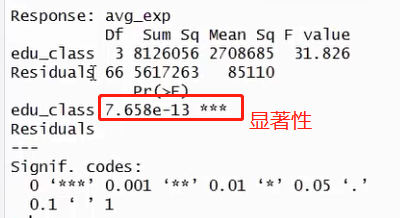
anova(lm(avg_exp～edu_class,data=cre))

##这里分析的数据是creditcard_exp.csv信用卡消费

##edu_class是学历等级

##先做下箱线图可以大致的看下是否相关

 

 2.2 多因数相关关系

比如将信用卡消费表，将年龄和学历一起进行相关

 

 三、交互项