卷积神经网络---分类问题

卷积神经网络简介

    卷积神经网络（Convolutional Neural Networks, CNN）是一种特殊的前馈神经网络，它来源于动物视觉的研究。在视觉皮层细胞中，存在这一个对外部视觉输入很敏感的区域，这片区域被称为感受野（receipt filed）。感受野收到的输入已以平铺的方式覆盖到整个视觉区域。一个神经元对感受野收到刺激后反馈的信号可以通过数学上的卷积运算来近似。卷积神经网络利用这个特质可以很好的处理视觉问题。

 

卷积神经网络结构

   卷积神经网络由输入层、卷积层、池化层、全连接层以及输出层组成，其结构如下图所示：

 

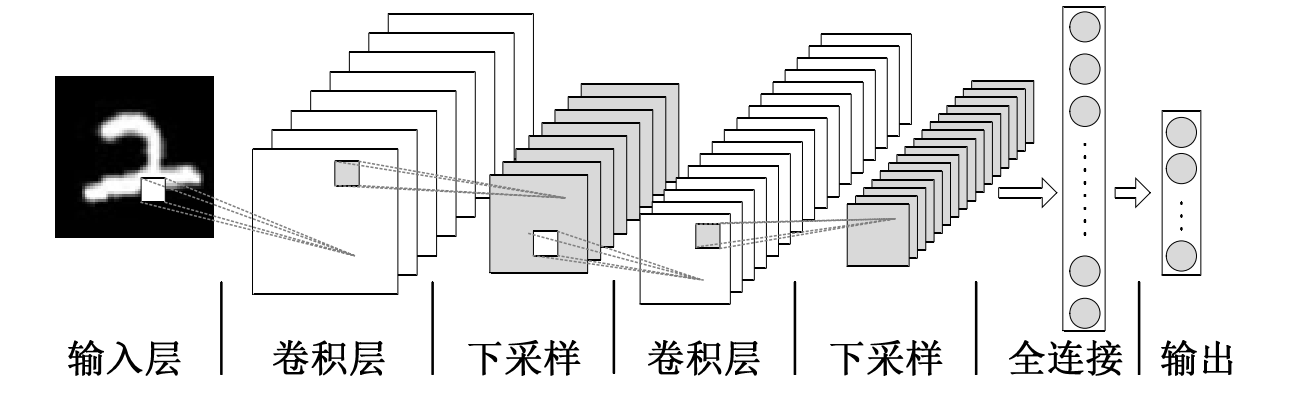
图1 卷积神经网络结构 

 

   针对图像数据X，首先进入输入层，输入层接收的张量形状为（image_height,image_width,image_channels）（不包括批次维度），输入层不对数据做过多的操作。输入层输出将作为下一层的输入，依次类推，进入卷积层后，通过过滤器对数据进行卷积运算，运算结果即是从数据中挖掘到特征，该结果称为特征图，随着网络的加深，模型挖掘的特征也在不断抽象化。

  在卷积神经网络中卷积层和池化层是彼此相邻的，池化层的主要作用是对数据进行下采样，为经过下采样的模型可能不足以获得可以进行分类的特征，而且只有卷积层会导致最后一层的特征图的参数过多，容易使模型过拟合。

  训练数据经过经过卷积层和池化层后进入最后的全连接层，注意以上图为例，最后一层下采样的输出形状与输入的形状是相同的，要进入全连接层，首先要先将特征图展平成一维的数据，然后进入全连接层。全连接层将获取到的特征整合，获取图像特征的高层含义，之后用于图像分类。

 

数据层级传递关系

  本部分将重点探讨数据在网络中的形状变化原因以及更层级的输入与输出情况，在此借助猫狗分类问题来进行解释。首先我们搭建一个有4个卷积层+4个最大池化层+2个全连接层的CNN模型，卷积核选为3×3，其具体结构如下：

 

 

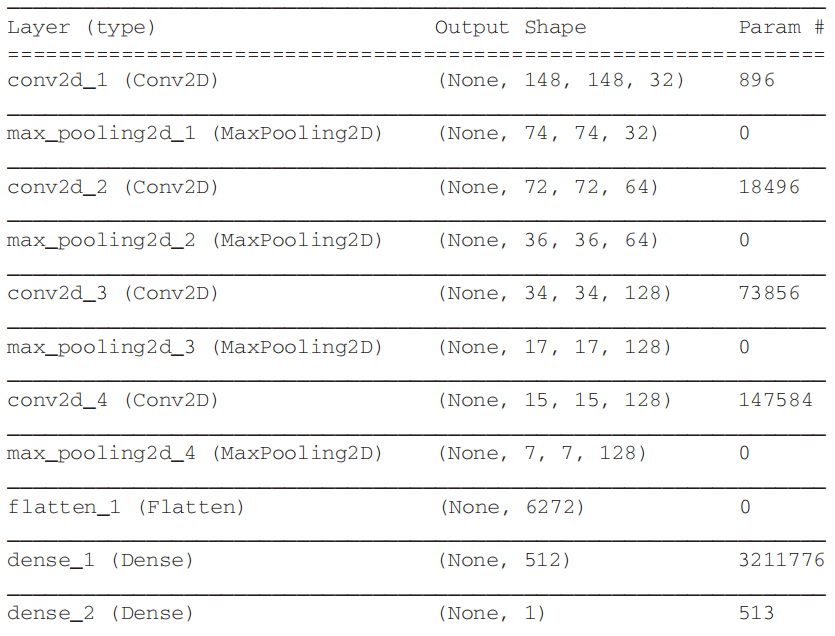
图2   模型网络结构

 

   由图可以看出，除了刚刚提到的层外还多了一个Flatten，这个层级就是用来将特征图展平为一维数据的。在本实例中，输入到网络中的图像形状为（150×150×3）,3表示颜色通道为RGB。经过第一个卷积层后，张量变成了（148×148×32），其长和宽分别减小2，通道数变为32，表示特征图在输入上计算了32个过滤器，（这里的过滤器可以理解为特征提取器，原则上是过滤器越多越好，这样提取到的特征也就越多，但限于设备，过滤器不宜过多），对于32个输出通道，每个通道中都包含一个148×148的数值网络，它是过滤器对输入的响应图，过滤器的具体计算过程将在下一部分介绍，特征图经过过滤器后，通道数因为过滤器数量的设置而增加，长和宽在运算过程中由于边界效应，分别减少了2。

  第一个卷积层的输出作为输入进入第一个池化层，池化过程又称为下采样，最大池化将特征图的尺寸缩减为原尺寸的一半，最大池化是从输入特征图中提取窗口，并输出每个通道的最大值，它的计算过程与卷积运算较为相似，详情将在池化原理中具体介绍。

  接着来的卷积层与池化层的特征图的形状依次类推，即卷积层长和宽个减小2，通道数随着层级增加（一般是根据一定的规律人为设置），池化层特征图的长宽缩减为原来的一半，通道数不变。

  再次观察模型层级结构图，发现最后一个池化层输出特征图形状为（7×7×128），通过展平操作后，特征图变为一维数据，即上述三个数相乘，（6272，），一维数据进入全连接层，全连接层的第一层由512个神经元组成（这里的512通常设置为2的指数倍，为经验参数），第二层全连接层的神经元数量为1位输出类别数。注，全连接层的训练参数为3211776，是由神经元个数乘以特征数得到的。

 

卷积原理

   与全连接层不同，卷积层从输入特征空间中学到的是局部模式，对于图像而言，学到的就是在输入图像的二维小窗口中发现的模式，如下图。对于卷积过程有两个重要参数，一是从输入中提取的图块尺寸，本实例中为3×3，另一个就是特征图的深度，可看成要提取的特征数。

                                            图3  图像可以分解成局部特征如边缘、纹理等                                                                            

   卷积的具体过程是过滤器在3D的特征图上滑动，每滑动一次计算一个卷积值，过程如下图所示

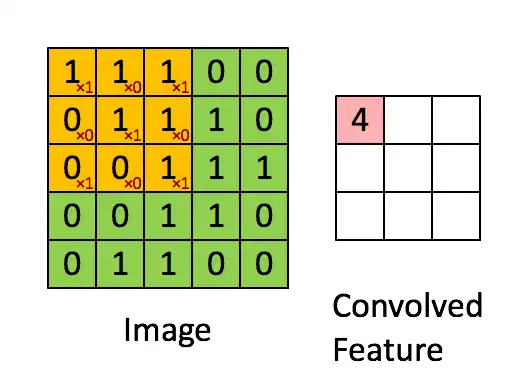         图4  卷积计算过程       

      

   由上图的卷积计算过程我们发现，原图像为5×5，在经过过滤器计算后，得到的是一个3×3的特征图，是因为过滤器在移动过程中，每次向某一方向移动一个单位，从起点运算到重点是，过滤器一共移动了5-(3-1)次，同理如果原图像是9×9，过滤器为5×5，那么最终得到的的特征图的边长为9-(5-1)。其计算原理是滤波器每次与图像同等大小的区域进行点乘，点乘后的结果再求和作为该区域的特征值，该操作即为卷积操作，如上图中第一个位置的4。当考虑深度后，计算过程如下图：

 

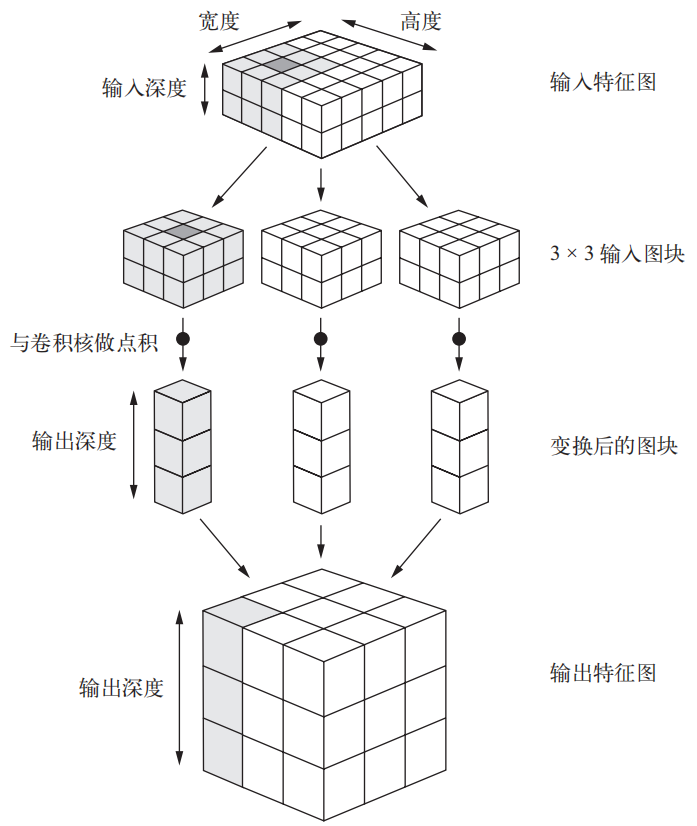
图5  卷积工作原理 

 

 

池化原理

   一般情况下，卷积神经网络在卷积层之间会周期性的插入池化层，其存在的主要意义是，通过池化操作来减少卷积层输出的特征向量，从而在最终模型训练时可以减少参数的训练，来防止过拟合。池化操作又叫作下采样，其过程与卷积相似，也是通过滑动一个特定区域，来运算，以最大池化操作为例，见下图，一个2×2的区域以2位步幅从左至右一次滑动，每次取区域中的最大值，因为是以2位步幅，所以最终下采样的结果是特征图的数量被缩小为原来的一半，不如原有4×4的特征图，经过池化后，得到2×2的特征图。

 

 

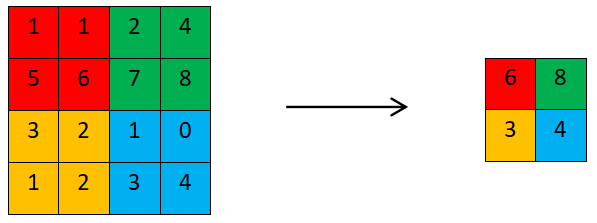
 图5  最大池化操作

 

 

全连接层原理

    全连接层一般出现在网络的最后，是一种传统的多层感知机网络。全连接层的每一个神经元与前一层网络的每一个神经元全连接。卷积层和池化层是从原始图像数据中提取抽象的特征，而全连接层正好与之相反，它是将前面层级获取的特征映射到标记空间，从而达到分类的目的。在实际操作中，全连接层可以通过卷积操作来实现，在本实例中，一共有两层全连接层，第一层共有512个神经元，第二层只有一个神经元，使用sigmoid激活函数来对某个类别的概率进行编码。