二叉树的相关遍历

一、进行查找操作的二叉树结构

 

 创建的二叉树：

 

 

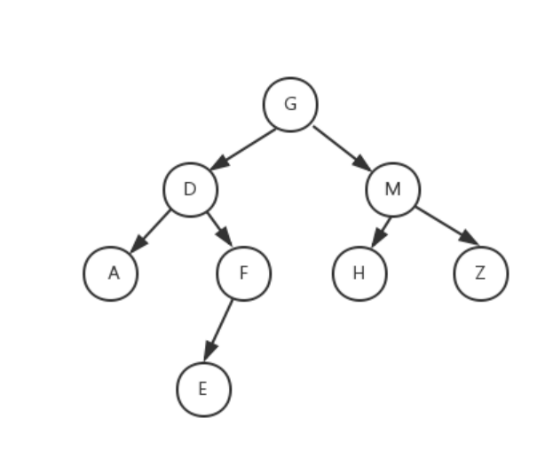
package com.zjl.test.hrtset;

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class TreeSort {
    public static void main(String[] args) {

        //创建一个简单的二叉树
        Node E = new Node('E');
        Node F = new Node('F');
        F.leftNode = E;
        Node A = new Node('A');
        Node D = new Node('D');
        D.leftNode = A;
        D.rightNode = F;
        Node H = new Node('H');
        Node Z = new Node('Z');
        Node m = new Node('M');
        m.leftNode = H;
        m.rightNode = Z;
        Node G = new Node('G');
        G.leftNode = D;
        G.rightNode = m;

        //前序遍历
//        Sort.preSort(G);
//        System.out.println();
//        Sort.preSort1(G);
        /*G->D->A->F->E->M->H->Z->
         G->D->A->F->E->M->H->Z->*/

        //中序遍历
//        Sort.midSort(G);
//        System.out.println();
//        Sort.midSort1(G);
        /*
        A->D->E->F->G->H->M->Z->
        A->D->E->F->G->H->M->Z->
        */

        //后序遍历
//        Sort.afterSort(G);
//        System.out.println();
//        Sort.afterSort1(G);
        /*A->E->F->D->H->Z->M->G->
        A->E->F->D->H->Z->M->G->*/

        //按层次输出
        Sort.levelSort(G);
        /*G->D->M->A->F->H->Z->E->*/


    }
}

class Node {
    public char data;
    public Node leftNode;
    public Node rightNode;

    public Node(char e) {
        this.data = e;
    }
}

class Sort {
    //先序排列（根左右）递归进行
    public static void preSort(Node node) {
        if (node == null) {
            return;
        }
        System.out.print(node.data + "->");
        preSort(node.leftNode);
        preSort(node.rightNode);
    }

    //先序排列（根左右）不使用递归，使用栈
    public static void preSort1(Node root) {
        //创建一个Node的栈，栈的作用就是用来保存根节点，利用栈先进后出的特点实现向后查找的功能
        Stack<Node> stack = new Stack<>();
        Node node = root;
        while (node != null || !stack.isEmpty()) {
            if (node != null) {
                //将根节点放入到栈中
                stack.push(node);
                System.out.print(node.data + "->");
                //根据先序遍历的特点，根左右（输出根，然后检查左是否为空，接着就是右）
                node = node.leftNode;
            } else {
                //说明此时的node节点为空，stack不为空，所以要返回到该节点的根节点，
                // 然后检查根节点的右节点的是否存在
                Node temp = stack.pop();
                node = temp.rightNode;
            }
        }
    }

    //中序遍历（左根右）递归进行
    public static void midSort(Node node) {
        //判断根节点不为空，如果为空不做处理，进程结束
        if (node != null) {
            //中序遍历先将最对二叉树的最左边进行遍历，如果左节点不存在了就输出该节点
            // 再查看该节点的右节点，将右节点当做一个新的节点，递归进行遍历
            midSort(node.leftNode);
            System.out.print(node.data + "->");
            midSort(node.rightNode);
        }
    }

    //中序遍历 （左根右） 非递归，使用栈保存对应根节点
    public static void midSort1(Node root) {
        //用栈保存根节点
        Stack<Node> stack = new Stack<>();
        Node node = root;
        //如果判断条件为空，并且栈中没有数据说明遍历二叉树完成
        while (node != null || !stack.isEmpty()) {
            if (node != null) {
                //节点不为空就继续寻找该节点对应的左节点
                stack.push(node);
                node = node.leftNode;
            } else {
                //当找到的左节点为空的时候就回到该左节点的根节点，输出该节点，
                // 然后遍历该节点对应的右节点并且按照顺序输出
                Node temp = stack.pop();
                System.out.print(temp.data + "->");
                node = temp.rightNode;
            }

        }
    }

    //后序遍历（左右根）递归进行
    public static void afterSort(Node node) {
        if (node != null) {
            afterSort(node.leftNode);
            afterSort(node.rightNode);
            System.out.print(node.data + "->");

        }
    }

    //后序遍历（左右根）非递归进行，使用栈保存对应根节点
    public static void afterSort1(Node root) {
        //设置两个临时节点，当做索引，cur当做游标，cur当做当前游标的节点的前一个节点
        Node cur, pre = null;
        Stack<Node> stack = new Stack<>();
        //将头结点加入到stack中
        stack.push(root);
        while (!stack.isEmpty()) {
            //查看栈中的栈顶，当做游标的开始信息
            cur = stack.peek();
            //判断条件(cur.rightNode == null && cur.leftNode == null)为true表示该游标所在的节点已经到达一个尾结点（没有左右孩子）
            //pre != null && (pre == cur.leftNode || pre == cur.rightNode)为true表示已经开始读取已经确定位置节点的父节点了
            //其中(pre == cur.leftNode || pre == cur.rightNode)用于确定游标所指向的就是上一个已经输出的节点的父节点
            if ((cur.rightNode == null && cur.leftNode == null) || pre != null && (pre == cur.leftNode || pre == cur.rightNode)) {
                System.out.print(cur.data + "->");
                //输出节点并将游标所指向的节点从栈中popo出去
                stack.pop();
                //将pre指向已经输出的节点，方便判断下一个节点的判断条件
                pre = cur;
            } else {
                //如果到达的不是最后一个节点或者是已经输出子节点的节点就将该节点判断该节点的左右存在情况，
                // 先判断右节点，原因是栈的栈入栈出特点是先进后出，刚好满足查找判断节点的输出条件（左右根）
                //只要该节点的左右孩子满足不为空，那就可以将节点按照顺序据继续放入栈中
                if (cur.rightNode != null) {
                    stack.push(cur.rightNode);
                }
                if (cur.leftNode != null) {
                    stack.push(cur.leftNode);
                }
            }
        }

    }

    //层次遍历（层次从上往下遍历，同一层从左往右遍历）
    public static void levelSort(Node node){
        Queue<Node> queue = new LinkedList<>();
        if (node == null) {
            return;
        }
        queue.add(node);
        while (!queue.isEmpty()) {
            //这里可以用poll(),remove()和peek()
            //其中peek()是查看和返回队列的(列首)第一个
            Node peek = queue.poll();
            System.out.print(peek.data+"->");
            if (peek.leftNode != null ) {
                queue.add(peek.leftNode);
            }
            if (peek.rightNode != null) {
                queue.add(peek.rightNode);
            }
            //remove和poll都是检索并删除队列的头部，只是头部为空时返回的不同
//            queue.remove();
//            queue.poll();
        }
    }
}