IfcBSplineCurveWithKnots

ifcbsprinecurvewithknots是一条样条曲线，它由样条函数参数化，其中明确给出了节点值。

注：定义根据ISO/CD 10303-42:1992

这是一种b样条曲线，其中明确给出了节点值。该子类型应用于表示非均匀B样条曲线，也可用于其他结类型。

让L表示结列表中d+k+2结中不同值的数目；L将被称为“结上索引”。设mj表示第j个不同结的多重性（即，重复次数）。然后：

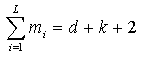
除第一个和最后一个外，所有结重数应在1，…，d范围内；第一个和最后一个可能具有最大值d+1。在计算基函数时，例如重数3的结u被解释为结数组中的序列u，u，u。

注：实体改编自b_样条曲线_，节点如ISO10303-42所定义。

IFC4中增加的新实体。

Formal Propositions

Rule	Description
ConsistentBSpline	The function IfcConstraintsParamBSpline returns TRUE if no inconsistencies in the parametrisation of the B-spline are found.
CorrespondingKnotLists	The number of elements in the knot multiplicities list shall be equal to the number of elements in the knots list.

 

#	Attribute	Type	Cardinality	Description	C
IfcRepresentationItem
	LayerAssignment	IfcPresentationLayerAssignment @AssignedItems	S[0:1]	Assignment of the representation item to a single or multiple layer(s). The LayerAssignments can override a LayerAssignments of the IfcRepresentation it is used within the list of Items.	X
	StyledByItem	IfcStyledItem @Item	S[0:1]	Reference to the IfcStyledItem that provides presentation information to the representation, e.g. a curve style, including colour and thickness to a geometric curve.	X
IfcGeometricRepresentationItem
IfcCurve
	Dim :=IfcCurveDim(SELF)	IfcDimensionCount	[1:1]	The space dimensionality of this abstract class, defined differently for all subtypes, i.e. for IfcLine, IfcConic and IfcBoundedCurve.	X
IfcBoundedCurve
IfcBSplineCurve
1	Degree	IfcInteger	[1:1]	The algebraic degree of the basis functions.	X
2	ControlPointsList	IfcCartesianPoint	L[2:?]	The list of control points for the curve.	X
3	CurveForm	IfcBSplineCurveForm	[1:1]	Used to identify particular types of curve; it is for information only.	X
4	ClosedCurve	IfcLogical	[1:1]	Indication of whether the curve is closed; it is for information only.	X
5	SelfIntersect	IfcLogical	[1:1]	Indication whether the curve self-intersects or not; it is for information only.	X
	UpperIndexOnControlPoints :=(SIZEOF(ControlPointsList) - 1)	IfcInteger	[1:1]	The upper index on the array of control points; the lower index is 0. This value is derived from the control points list.	X
	ControlPoints :=IfcListToArray(ControlPointsList,0,UpperIndexOnControlPoints)	IfcCartesianPoint	A[0:UpperIndexOnControlPoints]	The array of control points used to define the geometry of the curve. This is derived from the list of control points.	X
IfcBSplineCurveWithKnots
6	KnotMultiplicities	IfcInteger	L[2:?]	The multiplicities of the knots. This list defines the number of times each knot in the knots list is to be repeated in constructing the knot array.	X
7	Knots	IfcParameterValue	L[2:?]	The list of distinct knots used to define the B-spline basis functions.	X
8	KnotSpec	IfcKnotType	[1:1]	The description of the knot type. This is for information only.	X
	UpperIndexOnKnots :=SIZEOF(Knots)	IfcInteger	[1:1]	The upper index on the knot arrays; the lower index is 1.	X

EXPRESS Specification

ENTITY IfcBSplineCurveWithKnots
 SUPERTYPE OF(IfcRationalBSplineCurveWithKnots)
 SUBTYPE OF (IfcBSplineCurve);
  KnotMultiplicities : LIST [2:?] OF IfcInteger;
  Knots : LIST [2:?] OF IfcParameterValue;
  KnotSpec : IfcKnotType;
 DERIVE
  UpperIndexOnKnots : IfcInteger := SIZEOF(Knots);
 WHERE
  ConsistentBSpline : IfcConstraintsParamBSpline(Degree, UpperIndexOnKnots, UpperIndexOnControlPoints, KnotMultiplicities, Knots);
  CorrespondingKnotLists : SIZEOF(KnotMultiplicities) = UpperIndexOnKnots;
END_ENTITY;