2022“杭电杯”中国大学生算法设计超级联赛(4)
Link with Bracket Sequence II
给定n个数,\(x\)和\(-x\)表示一对括号,正的表示左括号。0可以改成任意括号编号。|括号编号|<=m。问组成括号序列的方案数。
f[0][i][j]表示i-j最外面是一层括号的方案,f[1][i][j]表示i-j由几个括号并列组成的方案
#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
int n, m, a[505], f[2][505][505]; // 0 -> (...) 1-> ()()
inline int mo(int x) { return x >= mod ? x - mod : x; }
int main() {
int T; scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i < n; ++i)
f[0][i + 1][i] = 1;
for (int l = 2; l <= n; ++l) {
for (int i = 1; i + l - 1 <= n; ++i) {
int j = i + l - 1;
f[0][i][j] = f[1][i][j] = 0;
if (a[i] + a[j] == 0) {
if (a[i] == 0)
f[0][i][j] = 1ll * m * (f[0][i + 1][j - 1] + f[1][i + 1][j - 1]) % mod;
else if (a[i] > 0) f[0][i][j] = mo(f[0][i + 1][j - 1] + f[1][i + 1][j - 1]);
} else if (a[i] == 0 && a[j] < 0 || a[j] == 0 && a[i] > 0) {
f[0][i][j] = mo(f[0][i + 1][j - 1] + f[1][i + 1][j - 1]);
}
for (int k = i; k < j; ++k)
f[1][i][j] = (1ll * f[0][i][k] * (f[0][k + 1][j] + f[1][k + 1][j]) + f[1][i][j]) % mod;
}
}
printf("%d\n", mo(f[0][1][n] + f[1][1][n]));
}
return 0;
}
Link with Equilateral Triangle
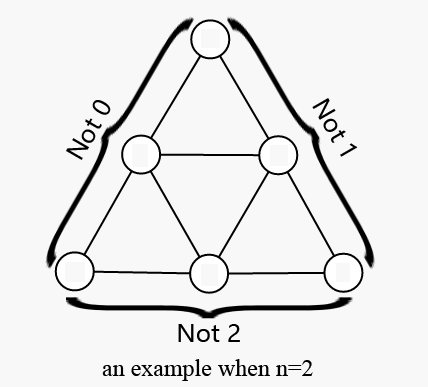
把0,1,2填入这个样子的图中,使单位三角形三个角上数字和不能是3的倍数,问是否可行。
意会考虑了一下最左边的两列,觉得不可能
BIT Subway
算术题
#include <bits/stdc++.h>
using namespace std;
//const double eps = 1e-7;
int main() {
int T; scanf("%d", &T);
while (T--) {
int n; scanf("%d", &n);
double s1 = 0, s2 = 0;
for (int i = 1; i <= n; ++i) {
double x; scanf("%lf", &x);
if (s2 < 100) s2 += x;
else if (s2 < 200) s2 += x * 0.8;
else s2 += x * 0.5;
if (s1 + x < 100) s1 += x;
else {
if (s1 < 100) {
x -= 100 - s1;
s1 = 100;
}
if (s1 + x * 0.8 < 200) s1 += x * 0.8;
else {
if (s1 < 200) {
x -= (200 - s1) / 0.8;
s1 = 200;
}
s1 += x * 0.5;
}
}
}
printf("%.3lf %.3lf\n", s1, s2);
}
return 0;
}
Climb Stairs
有n层楼,开始在0层,每层只能之多向上跳k层,或向下跳1层,不能重复走。起初有血量a0,每层有ai,只能去ai<=当前血量的层,去了血量增加ai,问能否走遍所有楼
发现跳的形式一定是从x向上到y,然后再向下把y以下的吃完,继续向上。而且容易证明y越低越好。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100000 + 5;
int T, n, k, a[N], LOG[N];
ll hp, suf[N], pre[N], st[N][17];
set<pair<ll, int> > ss;
ll ask(int l, int r) {
int len = r - l + 1;
return min(st[l][LOG[len]], st[r - (1 << LOG[len]) + 1][LOG[len]]);
}
int main() {
for (int i = 2; i <= 100000; ++i) LOG[i] = LOG[i >> 1] + 1;
int T; scanf("%d", &T);
while (T--) {
scanf("%d%lld%d", &n, &hp, &k);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
suf[n + 1] = 0;
for (int i = n; i >= 1; --i)
suf[i] = suf[i + 1] + a[i];
pre[0] = -1e18;
for (int i = 1; i <= n; ++i)
pre[i] = max(pre[i - 1], a[i] - suf[i + 1]);
for (int i = 1; i <= n; ++i)
st[i][0] = pre[i] + suf[i + 1];
for (int j = 1; j <= 16; ++j)
for (int i = 1; i + (1 << j) - 1 <= n; ++i)
st[i][j] = min(st[i][j - 1], st[i + (1 << j - 1)][j - 1]);
int now = 0, R = 0;
while (R < n) {
int l = R + 1, r = min(n, now + k), ret = -1;
while (l <= r) {
int mid = l + r >> 1;
if (ask(l, mid) <= hp) {
ret = mid;
r = mid - 1;
} else
l = mid + 1;
}
if (ret == -1) { now = -1; break; }
hp += suf[R + 1] - suf[ret + 1];
now = R + 1;
R = ret;
}
if (now == -1) puts("NO"); else puts("YES");
}
return 0;
}
Link is as bear
给n个数,每次可以把[l,r]中的数都变成\(a_l xor a_{l+1} xor ... xor a_r\),且保证原数组至少有两个数相等。
答案貌似是所有数能异或出来的最大值。



