notepad

4.21

高精度

struct Big {
	static const int s = 100000000;
	long long a[80], len;
	Big(int x = 0) {
		memset(a, 0, sizeof(a));
		len = 0;
		while (x) a[++len] = x % s, x /= s;
	}
	Big operator +(const Big &rhs) {
		Big c;
		c.len = max(len, rhs.len);
		long long j = 0;
		for (int i = 1; i <= c.len; ++i) {
			j = a[i] + rhs.a[i] + j;
			c.a[i] = j % s;
			j /= s;
		}
		if (j) c.a[++c.len] = j;
		return c;
	}
	Big operator *(const Big &rhs) {
		Big c;
		c.len = len + rhs.len;
		for (int i = 1; i <= len; ++i)
			for (int j = 1; j <= rhs.len; ++j)
				c.a[i + j - 1] += a[i] * rhs.a[j];
		for (int i = 1; i <= c.len; ++i) {
			c.a[i + 1] += c.a[i] / s;
			c.a[i] %= s;
		}
		while (len && c.a[c.len] == 0) --c.len;
		return c;
	}
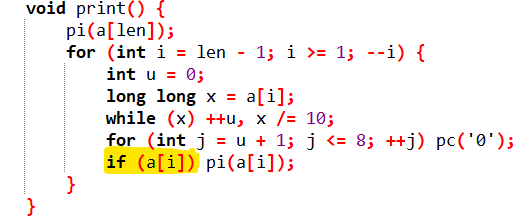
	void print() {
		pi(a[len]);
		for (int i = len - 1; i >= 1; --i) {
			int u = 0;
			long long x = a[i];
			while (x) ++u, x /= 10;
			for (int j = u + 1; j <= 8; ++j) pc('0');
			if (a[i]) pi(a[i]);
		}
	}
	long long operator %(int mod) {
		long long j = 0;
		for (int i = len; i >= 1; --i)
			j = (j * s + a[i]) % mod;
		return j;
	}
	Big operator /=(int mod) {
		long long j = 0;
		for (int i = len; i >= 1; --i) {
			j = j * s + a[i];
			a[i] = j / mod;
			j %= mod;
		}
		while (len && a[len] == 0) --len;
		return *this;
	}
}

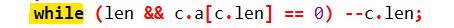
4.22

树hash

int dfs(int u, int fa) {
	vector<int> s;
	int ret = 2333ll;
	for (int v : G[u])
		if (v != fa)
			s.push_back(1ll * dfs(v, u) * G[v].size() % mod);
	sort(s.begin(), s.end());
	for (int x : s)
		ret = ((ret * 2333ll) ^ x) % mod;
	return ret;
}

4.27

"如果图不是二分图，就说明图中一定有长度为奇数的环"

习惯性%mod。。。

4.28

给n\(*\)m的矩阵，每个元素是0/1。对于每个(x,y)，求有多少x*y的子矩阵全是1。([51nod1291]Farmer)
单调栈，可以优化到O(nm)。

int main() {
  n = gi(), m = gi();
  for (int i = 1; i <= n; ++i) {
    f[0] = i;
    top = 0;
    for (int j = 1; j <= m; ++j) {
      char c;
      while (c = gc(), c < '0' || c > '1');
      f[j] = c == '1' ? f[j] : i;
      while (top && f[j] >= f[s[top]]) --top;
      s[++top] = j;
      for (int k = 1; k <= top; ++k) {
        for (int x = f[s[k]] + 1; x <= f[s[k - 1]]; ++x)              //第二个代码
	  for (int y = s[k - 1] + 1; y <= j; ++y)                     //用差分
	    ++ans[i - x + 1][j - y + 1];                              //优化了该部分
      }
    }
  }
  for (int i = 1; i <= n; ++i) {
    for (int j = 1; j <= m; ++j)
      cout << ans[i][j] << " ";
    cout << endl;
  }
}

以下是O(n^3)

void add(int sx, int sy, int ex, int ey) {
	++ans[sx][sy];
	--ans[sx][ey + 1];
	--ans[ex + 1][sy];
	++ans[ex + 1][ey + 1];
}
int main() {
	n = gi(), m = gi();
	for (int i = 1; i <= n; ++i) {
		f[0] = i;
		top = 0;
		for (int j = 1; j <= m; ++j) {
			char c;
			while (c = gc(), c < '0' || c > '1');
			f[j] = c == '1' ? f[j] : i;
			while (top && f[j] >= f[s[top]]) --top;
			s[++top] = j;
			for (int k = 1; k <= top; ++k) {
				add(i - f[s[k - 1]] + 1, 1, i - f[s[k]], j - s[k - 1]);    //用tag[top]表示top以前的元素应该进行几次add
			}
		}
	}
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j)
			cout << (ans[i][j] += ans[i - 1][j] + ans[i][j - 1] - ans[i - 1][j - 1]) << " ";
		cout << endl;
	}
	return 0;
}

以下O(nm)：

void add(int sx, int sy, int ex, int ey, int t) {
	ans[sx][sy] += t, ans[sx][sy + 1] -= t;
	--ans[sx][ey + 1], ++ans[sx][ey + t + 1];
	ans[ex + 1][sy] -= t, ans[ex + 1][sy + 1] += t;
	++ans[ex + 1][ey + 1], --ans[ex + 1][ey + t + 1];
}
int main() {
	n = gi(), m = gi();
	for (int i = 1; i <= n; ++i) {
		f[0] = i;
		top = 0;
		for (int j = 1; j <= m; ++j) {
			char c;
			while (c = gc(), c < '0' || c > '1');
			f[j] = c == '1' ? f[j] : i;
			while (top && f[j] >= f[s[top]]) {
				add(i - f[s[top - 1]] + 1, 1, i - f[s[top]], s[top] - s[top - 1], tag[top]);
				tag[top - 1] += tag[top];
				--top;
			}
			s[++top] = j;
			tag[top] = 1;
		}
		while (top) {
			add(i - f[s[top - 1]] + 1, 1, i - f[s[top]], s[top] - s[top - 1], tag[top]);
			tag[top - 1] += tag[top];
			--top;
		}
	}
	for (int i = 1; i <= n; ++i)
		for (int j = 1; j <= m; ++j)
			ans[i][j] += ans[i][j - 1];
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j)
			cout << (ans[i][j] += ans[i - 1][j] + ans[i][j - 1] - ans[i - 1][j - 1]) << " ";
		cout << endl;
	}
	return 0;
}

5.18

旋转treap

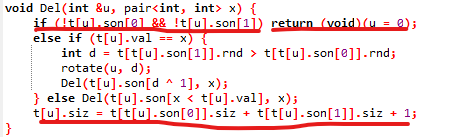
第一处不要判siz=1，第二处要return（不然会被第三处影响），第三处不要--siz，重新计算，还有rotate要引用u。

5.19

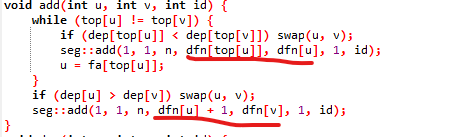
树剖，看清楚是覆盖点还是覆盖边。覆盖边只需最后+1

5.24

&的优先级没有>高
这样写
sort(a + 1, a + n + 1, [&](ll x, ll y) { return (x & (1ll << i) - 1) > (y & (1ll << i) - 1);
不是这样
sort(a + 1, a + n + 1, [&](ll x, ll y) { return x & (1ll << i) - 1 > y & (1ll << i) - 1;

5.25

注意：pdiv的B.resize(size(a) - size(b) + 1);求逆保证常数不为0;pexp的部分求ln注意
多项式板子（插值）

#include <bits/stdc++.h>
#define clr(f, n) memset(f, 0, sizeof(int) * (n))
#define cpy(f, g, n) memcpy(f, g, sizeof(int) * (n))
using namespace std;
namespace cyl {
typedef long long ll;
const int mod = 998244353, inv3 = (mod + 1) / 3, N = 700000;
template<class T> T max(const T &x, const T &y) { return x > y ? x : y; }
template<class T> T min(const T &x, const T &y) { return x < y ? x : y; }
template<class T> int size(const T &x) { return x.size(); }
int mo(int x) { return x >= mod ? x - mod : x; }
int mo2(int x) { return x < 0 ? x + mod : x; }
int fpow(int a, int b) {
	int ret = 1;
	for (; b; b >>= 1, a = 1ll * a * a % mod)
		if (b & 1)
			ret = 1ll * ret * a % mod;
	return ret;
}
namespace IO {
	const int l = (int)1e6;
	char buf[l], *p, *q, out[l], *t = out;
	void flush() { fwrite(out, 1, t - out, stdout); t = out; }
	void pc(char c) { *t++ = c; if (t - out == l) flush(); }
	char gc() { return p == q && (q = (p = buf) + fread(buf, 1, l, stdin), p == q) ? -1 : *p++; }
	int gi() {
		int x = 0, f = 1; char c = gc();
		while (c > -1 && c < '0' || c > '9') { if (c == '-') f = 0; c = gc(); }
		if (c == -1) return 0;
		while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - 48, c = gc();
		return f ? x : -x;
	}
	template<class T> void pi(T x) {
		static int a[100];
		if (x < 0) pc('-'), x = -x;
		if (x == 0) pc('0');
		else {
			int len = 0;
			while (x) a[++len] = x % 10, x /= 10;
			while (len) pc(a[len--] + 48);
		}
	}
	struct F { ~F() { flush(); } } flusher;
}
using IO::gi;
using IO::pi;
using IO::pc;
namespace poly {
	struct vec : public vector<int> { using vector::vector; };
	int rev[N << 2], inv[N << 2], lim;
	void init() {
		inv[1] = 1;
		for (int i = 2; i < N << 2; ++i) inv[i] = 1ll * inv[mod % i] * (mod - mod / i) % mod;
	}
	void get(int n) {
		static int last = 1;
		if (last == n) return; last = n;
		for (int i = 1; i < n; ++i) rev[i] = rev[i >> 1] >> 1 | ((i & 1) ? n >> 1 : 0);
	}
	void ntt(int *a, int n, int t) {
		get(n);
		static int w[N << 2]; w[0] = 1;
		for (int i = 1; i < n; ++i) if (i < rev[i]) swap(a[i], a[rev[i]]);
		for (int l = 2; l <= n; l <<= 1) {
			int W = fpow(t == 1 ? 3 : inv3, (mod - 1) / l), ll = l >> 1;
			for (int i = 1; i < ll; ++i) w[i] = 1ll * w[i - 1] * W % mod;
			for (int i = 0; i < n; i += l)
				for (int j = 0; j < ll; ++j) {
					int x = a[i + j], y = 1ll * a[i + ll + j] * w[j] % mod;
					a[i + j] = mo(x + y), a[i + ll + j] = mo2(x - y);
				}
		}
		if (t == -1) for (int i = 0; i < n; ++i) a[i] = 1ll * a[i] * inv[n] % mod;
	}
	vec operator +(const vec &a, const vec &b) {
		vec c(a); c.resize(max(size(a), size(b)));
		for (int i = 0; i < size(b); ++i) c[i] = mo(c[i] + b[i]);
		return c;
	}
	vec operator -(const vec &a, const vec &b) {
		vec c(a); c.resize(max(size(a), size(b)));
		for (int i = 0; i < size(b); ++i) c[i] = mo2(c[i] - b[i]);
		return c;
	}
	vec operator *(const vec &a, const int &b) {
		vec c(a);
		for (int i = 0; i < size(a); ++i) c[i] = 1ll * c[i] * b % mod;
		return c;
	}
	vec operator *(const vec &a, const vec &b) {
		static int A[N << 2], B[N << 2];
		cpy(A, &a[0], size(a));
		cpy(B, &b[0], size(b));
		vec c; c.resize(min(lim, size(a) + size(b) - 1));
		int n = 1; for (; n < size(a) + size(b) - 1; n <<= 1);
		ntt(A, n, 1), ntt(B, n, 1);
		for (int i = 0; i < n; ++i) A[i] = 1ll * A[i] * B[i] % mod;
		ntt(A, n, -1);
		cpy(&c[0], A, size(c));
		clr(A, n), clr(B, n);
		return c;		
	}
	void pinv(const vec &a, vec &b, int n) {
		if (n == 1) b.push_back(fpow(a[0], mod - 2));
		else {
			pinv(a, b, n + 1 >> 1);
			vec sa; sa.resize(n);
			cpy(&sa[0], &a[0], n);
			b = b * 2 - b * b * sa;
			b.resize(n);
		}
	}
	vec pinv(const vec &a) {
		vec c; pinv(a, c, size(a));
		return c;
	}
	vec der(const vec &a) {
		vec c(a);
		for (int i = 1; i < size(c); ++i) c[i - 1] = 1ll * c[i] * i % mod;
		c[size(c) - 1] = 0;
		return c;
	}
	vec ints(const vec &a) {
		vec c(a);
		for (int i = size(c) - 1; i > 0; --i) c[i] = 1ll * c[i - 1] * inv[i] % mod;
		c[0] = 0;
		return c;
	}
	vec ln(const vec &a) { return ints(der(a) * pinv(a)); }
	void pexp(const vec &a, vec &b, int n) {
		if (n == 1) b.push_back(1);
		else {
			pexp(a, b, n + 1 >> 1);
			vec lnb(b); lnb.resize(n);
			lnb = ln(lnb); lnb.resize(n);
			for (int i = 0; i < size(lnb); ++i) lnb[i] = mo(mod - lnb[i] + a[i]);
			++lnb[0];
			b = b * lnb;
			b.resize(n);
		}
	}
	vec pexp(const vec &a) {
		vec c; pexp(a, c, size(a));
		return c;
	}
	void psqrt(const vec &a, vec &b, int n) {
		if (n == 1) assert(a[0] == 1), b.push_back(1);
		else {
			psqrt(a, b, n + 1 >> 1);
			vec sa; sa.resize(n);
			cpy(&sa[0], &a[0], n);
			b = b - (b * b - sa) * pinv(b * 2);
			b.resize(n);
		}
	}
	vec psqrt(const vec &a) {
		vec b; psqrt(a, b, size(a));
		return b;
	}
	vec pdiv(const vec &a, const vec &b) {
		vec A(a.rbegin(), a.rend()), B(b.rbegin(), b.rend());
		B.resize(size(a) - size(b) + 1);
		vec c = A * pinv(B); c.resize(size(a) - size(b) + 1);
		reverse(c.begin(), c.end());
		return c;
	}
	vec pmod(const vec &a, const vec &b) {
		vec d = a - b * pdiv(a, b); d.resize(size(b) - 1);
		return d;
	}
}
poly::vec p[N << 2], a;
int n, m, x[N << 2], y[N << 2], id[N], g[N];
void solve(int l, int r, int o) {
	if (l == r) {
		p[o] = poly::vec(2);
		p[o][0] = mod - x[l];
		p[o][1] = 1;
		id[l] = o;
		return;
	}
	int mid = l + r >> 1;
	solve(l, mid, o << 1);
	solve(mid + 1, r, o << 1 | 1);
	p[o] = p[o << 1] * p[o << 1 | 1];
}
void solve(int l, int r, int o, const poly::vec &a) {
	if (r - l <= 350) {
		for (int i = l; i <= r; ++i) {
			int buf = 1;
			for (int j = 0; j < size(a); ++j) {
				g[i] = (1ll * buf * a[j] + g[i]) % mod;
				buf = 1ll * buf * x[i] % mod;
			}
		}
		return;
	}
	int mid = l + r >> 1;
	solve(l, mid, o << 1, poly::pmod(a, p[o << 1]));
	solve(mid + 1, r, o << 1 | 1, poly::pmod(a, p[o << 1 | 1]));
}
poly::vec work(int l, int r, int o) {
	if (l == r) return poly::vec(1, 1ll * y[l] * fpow(g[l], mod - 2) % mod);
	int mid = l + r >> 1;
	return p[o << 1 | 1] * work(l, mid, o << 1) + p[o << 1] * work(mid + 1, r, o << 1 | 1);
}
int main() {
//	freopen("data.in", "r", stdin);
//	freopen("my.out", "w", stdout);
	poly::init();
	n = gi();
	poly::lim = n + 1;
	for (int i = 1; i <= n; ++i) x[i] = gi(), y[i] = gi();
	solve(1, n, 1);
	solve(1, n, 1, poly::der(p[1]));
	poly::vec c = work(1, n, 1);
	for (int i = 0; i < n; ++i) pi(c[i]), pc(' ');
	return 0;
}
} int main() { return cyl::main(); }

5.26

1.

\(\begin{aligned}\binom{2i}{i}=\binom{-1/2}{i}(-4)^i\end{aligned}\)

2.

\(\begin{aligned}F(x)=\frac{A(x)}{B(x)}\end{aligned}\)

设\(z_i(i=1,2,...,m)\)为方程\(B^R(x)=0\)的解，那么

\(\begin{aligned}\big [x^n\big ]F(x)=\sum_{i=1}^m\frac{-z_iA(\frac{1}{z_i})}{B'(\frac{1}{z_i})}z_i^n\end{aligned}\)

5.28

预处理了1-k的逆元，用了inv[3]，防止k<3。

5.30

记得把cerr，debug去掉。卡时间

6.3

priority_queue好像比手写二叉堆还慢。vector好像比数组慢很多

6.24

加密前不超过1e9，理解成解密前不超过1e9？犯贱了，能开longlong要开int

6.27

返回值类型别搞错了
template int cmin(T &x, const T &y) { return x > y ? x = y, 1 : 0; }
template T max(const T &x, const T &y) { return x > y ? x : y; }