2021.3.25

\(\mathcal{A}\)
积性函数的积、迪利克雷卷积都是积性的。
而且：设\(f(n)\)，\(g(n)\)是积性函数，则\(h(n)=\begin{aligned}\sum_{d|n}f(d)g(d)\end{aligned}\)也是积性函数。
\(\mathcal{B}\)
\(\begin{aligned}f(n)=\sum_{d|n}\mu(d)\frac{n}{d}\end{aligned}\)是积性函数。

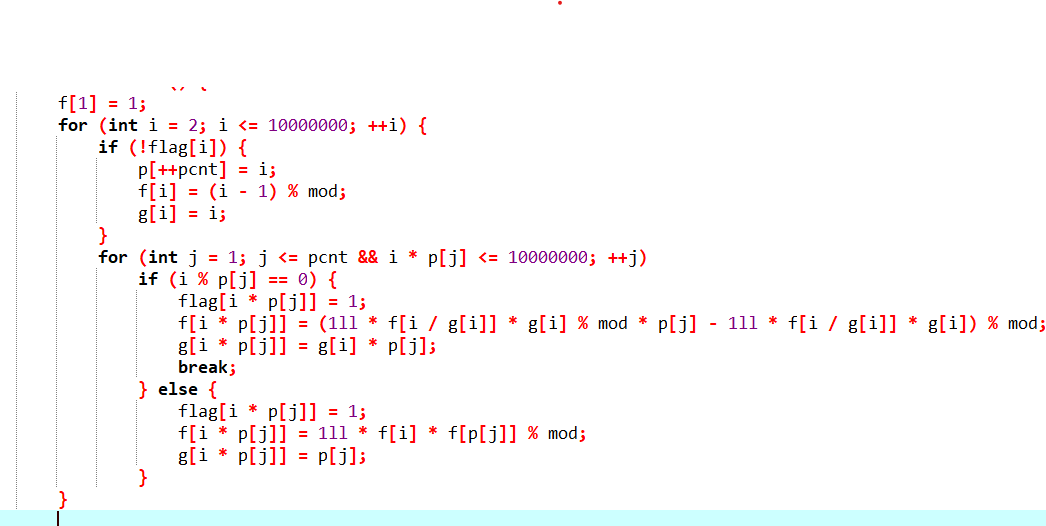
\(\begin{aligned}f(n)=\sum_{d|n}\mu(d)d\end{aligned}\)是积性函数。

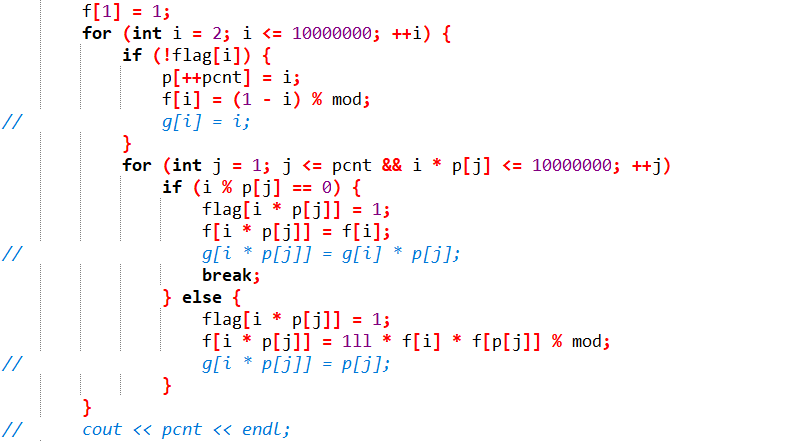
\(\mathcal{C}\)


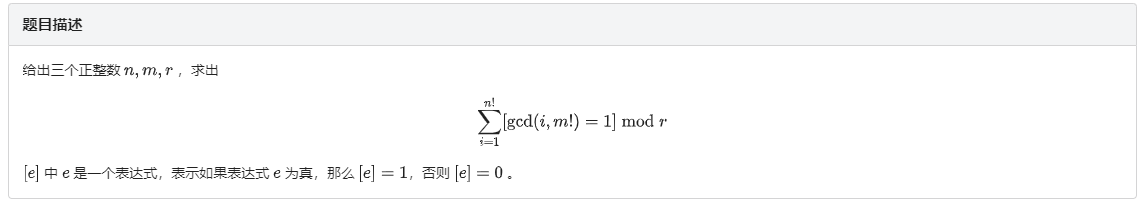
n!的质因子很少。

#include <bits/stdc++.h>
using namespace std;
namespace cxcyl {
	const int tot = (int)1e7;
	int mod, p[700005], pcnt, f[700005][2], T, jc[tot + 5];
	bool flag[tot + 5];
	inline int fpow(int a, int b) {
		int ret = 1;
		for (; b; b >>= 1, a = 1ll * a * a % mod)
			if (b & 1)
				ret = 1ll * ret * a % mod;
		return ret;
	}
	inline int main() {
		int T;
		scanf("%d%d", &T, &mod);
		for (int i = 2; i <= tot; ++i) {
			if (!flag[i])
				p[++pcnt] = i;
			for (int j = 1; j <= pcnt && i * p[j] <= tot; ++j) {
				flag[i * p[j]] = 1;
				if (i % p[j] == 0) break;
			}
		}
		jc[0] = 1;
		for (int i = 1; i <= tot; ++i)
			jc[i] = 1ll * jc[i - 1] * i % mod;
		f[0][1] = 1;
		for (int i = 1; i <= pcnt; ++i) {
			f[i][0] = (f[i - 1][0] + 1ll * f[i - 1][1] * fpow(p[i], mod - 2)) % mod;
			f[i][1] = (f[i - 1][1] + 1ll * f[i - 1][0] * fpow(p[i], mod - 2)) % mod;
		}
		while (T--) {
			int n, m;
			scanf("%d%d", &n, &m);
			int l = 0, r = pcnt;
			while (l < r) {
				int mid = l + 1 + r >> 1;
				if (p[mid] <= m)
					l = mid;
				else
					r = mid - 1;
			}
			printf("%lld\n", (1ll * jc[n] * (f[l][1] - f[l][0]) % mod + mod) % mod);
		}
		return 0;
	}
} int main() { return cxcyl::main(); }

\(\mathcal{D}\)
函数返回值不是void别忘了return