线段树的那些事
作为一名蒟蒻,竟然学会了线段树,也是神奇。。
现在就来交流一下我对线段树的一些认识:
First:
1.线段树是一种数据结构,每个节点储存一个区间的信息
2.可以用来优化DP、求区间最值等
3.递归求解,从根节点开始往下递归
4.用空间换时间
Second:
1.主要函数步骤:
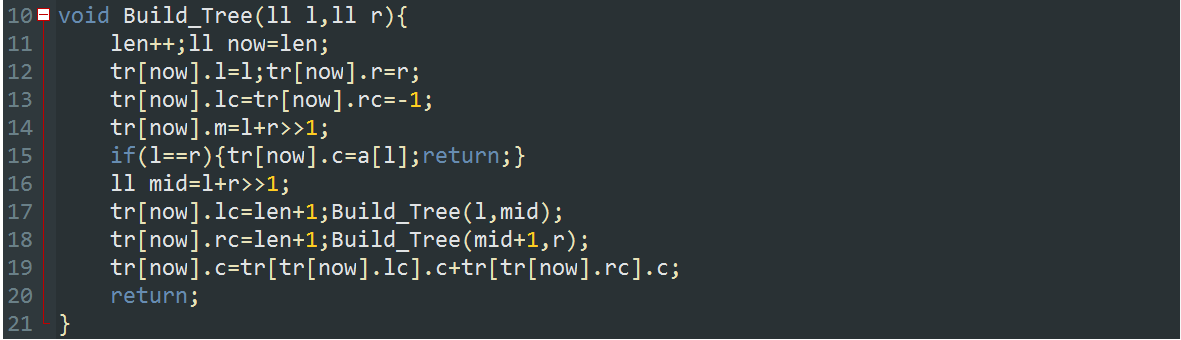
这是建树函数,其中l,r表示构造的区间,lc,rc表示这个节点的左节点和右节点的编号,c为特征值(可以替换)
step1:
将当前节点的编号记录,然后确定区间范围。
step2:
判断区间大小是否为1,如果是的话就可以直接赋值了,然后return
step3:
取当前区间的mid,然后再分成左右子树开始建树。
step4:
最后更新当前节点的特征值
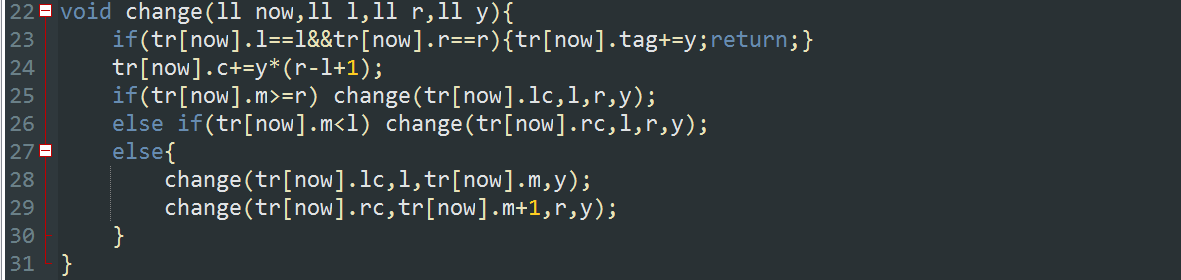
这个是修改区间的函数:
step1:
首先判断是不是相等,如果是的话就可以直接丢tag上然后return了
step2:
接着判断左子树还是右子树要修改,左子树递归
step3:
右子树递归
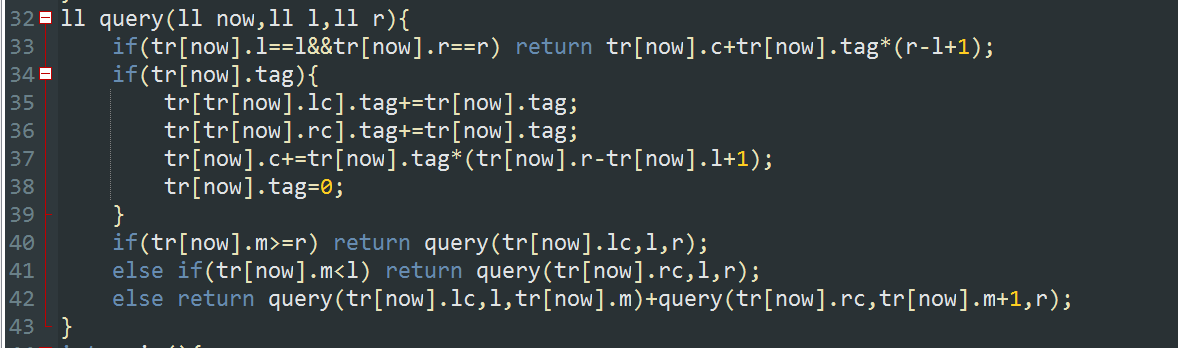
这个是区间求和的函数:
step1:
如果当前节点与所求区间相等,那么直接返回(记住要加上tag值)
step2:
如果当前点有tag的话,那么就把tag往下传,并且加入特征值中,然后清零
step3:
接着判断所求区间在左子树还是右子树中,然后return值;如果两个都有的话,那就加起来
2.优化
目前蒟蒻会的唯一优化是lazy tag,适用于区间修改等问题中
lazy思想:
由于每次区间修改都要递归到叶子节点,很烦,很慢,所以干脆就记录下当前节点要加多少,等到调用的时候再加上
但是要注意query求和时需要把标记往下传,并且加入特征值,清零,不然之后会重复计算
Third:
来看看一些线段树的水题:
题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数加上x
2.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式:
输出包含若干行整数,即为所有操作2的结果。
输入输出样例
输入样例:
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4
输出样例:
11
8
20
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=1000,M<=10000
对于100%的数据:N<=100000,M<=100000
key:
这道题目是懒标记的模板,可以用线段树+懒标记求解
1.开始建树,特征值C表示当前节点的权值
2.对于询问1,调用change函数,递归打上懒标记(需要判断区间是否相等)
3.对于询问2,调用query函数,对l~r求和,不断递归,直到能够直接求特征值为止
my code:
#include<bits/stdc++.h> #define maxn 100010 #define for(a,b) for(int i=a;i<=b;i++) #define ll long long using namespace std; ll len,n,Q,a[maxn],p,l,r,x; struct node{ ll l,r,lc,rc,c,tag,m; }tr[maxn<<2]; void Build_Tree(ll l,ll r){ len++;ll now=len; tr[now].l=l;tr[now].r=r; tr[now].lc=tr[now].rc=-1; tr[now].m=l+r>>1; if(l==r){tr[now].c=a[l];return;} ll mid=l+r>>1; tr[now].lc=len+1;Build_Tree(l,mid); tr[now].rc=len+1;Build_Tree(mid+1,r); tr[now].c=tr[tr[now].lc].c+tr[tr[now].rc].c; return; } void change(ll now,ll l,ll r,ll y){ if(tr[now].l==l&&tr[now].r==r){tr[now].tag+=y;return;} tr[now].c+=y*(r-l+1); if(tr[now].m>=r) change(tr[now].lc,l,r,y); else if(tr[now].m<l) change(tr[now].rc,l,r,y); else{ change(tr[now].lc,l,tr[now].m,y); change(tr[now].rc,tr[now].m+1,r,y); } } ll query(ll now,ll l,ll r){ if(tr[now].l==l&&tr[now].r==r) return tr[now].c+tr[now].tag*(r-l+1); if(tr[now].tag){ tr[tr[now].lc].tag+=tr[now].tag; tr[tr[now].rc].tag+=tr[now].tag; tr[now].c+=tr[now].tag*(tr[now].r-tr[now].l+1); tr[now].tag=0; } if(tr[now].m>=r) return query(tr[now].lc,l,r); else if(tr[now].m<l) return query(tr[now].rc,l,r); else return query(tr[now].lc,l,tr[now].m)+query(tr[now].rc,tr[now].m+1,r); } int main(){ scanf("%lld%lld",&n,&Q); for(1,n)scanf("%lld",&a[i]); Build_Tree(1,n); for(1,Q){ scanf("%lld%lld%lld",&p,&l,&r); if(p==1){ scanf("%lld",&x); change(1,l,r,x); } else printf("%lld\n",query(1,l,r)); } return 0; }




