Splay学习笔记
n(n<=500000)个数,要求维护区间加,区间查询
很简单,用线段树/树状数组随便写写就能过
n(n<=500000)个数,维护插入、删除、找区间第K大/小
用平衡树/set也能过
n(n<=500000)个数,维护区间翻转,区间查询,插入,删除
这个时候就需要用到伸展树(Splay)
splay是一种极(常)灵(数)活(大)的数据结构,它能够维护线段树的部分操作和平衡树的操作
它的美妙之处在于能够旋转,从而完成一系列操作
它的旋转和平衡树的只转一次不同,它可以进行双旋操作来保证较优秀的时间复杂度(但常数还是大)
双旋操作是基于单旋的
首先是单旋:

和平衡树相同
然后是双旋:
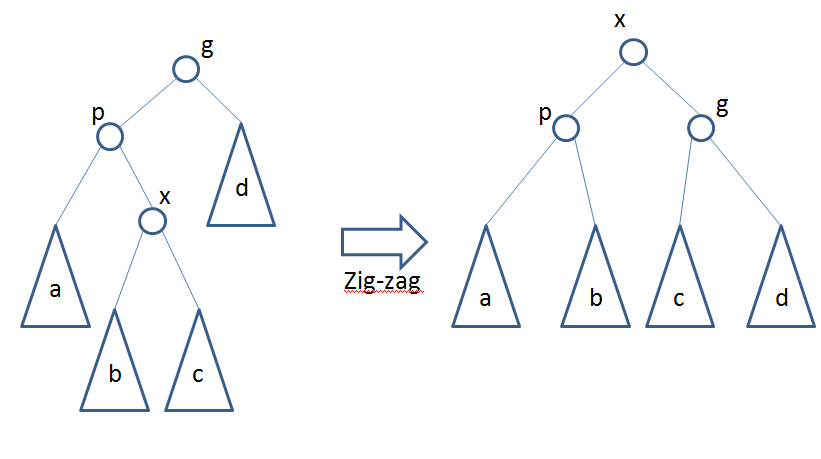
当p不是根节点,且x和p同为左孩子或右孩子时进行Zig-Zig操作。
当x和p同为左孩子时,依次将p和x右旋;
当x和p同为右孩子时,依次将p和x左旋。

当p不是根节点,且x和p不同为左孩子或右孩子时,进行Zig-Zag操作。
当p为左孩子,x为右孩子时,将x左旋后再右旋。
当p为右孩子,x为左孩子时,将x右旋后再左旋。
有了单旋和双旋就可以进行splay操作:
int get(int o){return tree[tree[o].fa].son[1]==o;}
void rotate(QAQ o){
int fa=tree[o].fa,ff=tree[fa].fa;
int pd=get(o);
if(ff) tree[ff].son[get(fa)]=o;
tree[o].fa=ff;
tree[fa].son[pd]=tree[o].son[1-pd];
tree[tree[o].son[1-pd]].fa=fa;
tree[fa].fa=o;tree[o].son[1-pd]=fa;
push_up(fa);push_up(o);
}
void splay(int o,int goal){
//goal是目标节点的父节点,为防止旋转之后导致节点更换带来的影响
while(tree[o].fa!=goal){
int fa=tree[o].fa,ff=tree[fa].fa;
if(ff!=goal) if(tree[ff].son[1]==fa ^ tree[fa].son[1]==o) rotate(o);
else rotate(fa);
rotate(o);
}
if(!goal) rot=o;//换根
push_up(o);
}
进行区间操作[l,r]时,常常把节点l-1转到根,r+1转到根的右儿子,这样根的右儿子的左儿子就是操作区间 ,并且常常添加虚拟节点0和n+1来进行[1,n]的操作
区间翻转就直接交换左右儿子
区间加直接加lazy标记
还能查询某一个值的排名:找到节点,转到根,根的做儿子大小+1就是排名
注意:splay中有些操作不能同时进行,例如求第K大和区间操作就不能同时进行,因为前一种操作改变了原序列顺序,后一个操作要求不能改变,这样就发生冲突。splay旋转仅仅是改变树的形状,并没有改变原序列顺序(树的中序遍历)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号